Second-order effects involve the analysis of a structure based on the deformed geometry. In other words, second-order analysis recognizes the deflection in a structure due to an externally applied load, and determines its effect on the internal forces generated thereof. The magnitude at which the internal forces in a structure increase due to second-order effects depend on the geometry, stiffness, and support conditions of the structure. This is usually employed in the verification of the stability of steel structures against phenomena such as buckling.
The sensitivity of a frame to second order effects may be illustrated simply by considering one ‘bay’ of a multi-storey building in simple construction (i.e. with pinned connections between beams and columns); the bay is restrained laterally by a spring representing the bracing system. First and second order displacements are illustrated below.
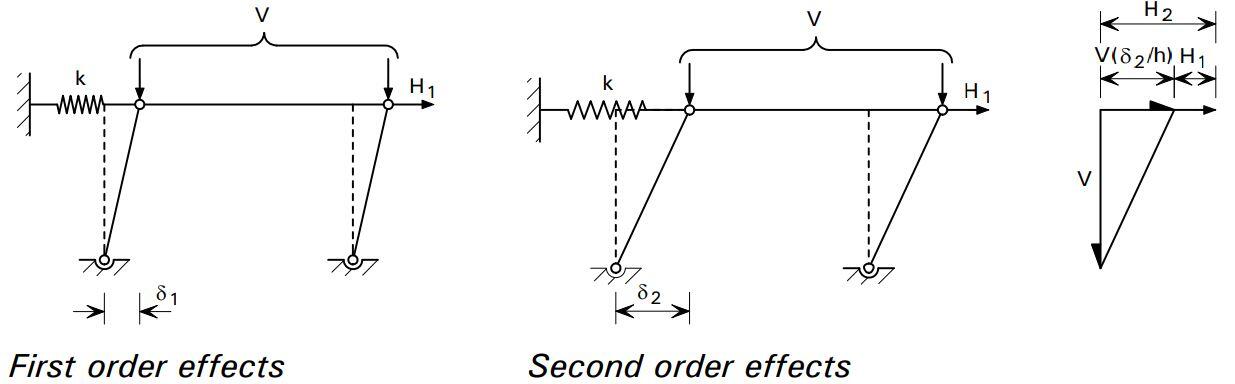
For first order effects;
kδ1 = H1
For second order effects;
kδ2 = H1 +V(δ2 / h) = H2
On rearranging the equation for second order effects, the equilibrium condition can be expressed as;
H2 = H1[1 / (1 – V/kh)]
Hence, it can be observed that if the stiffness of the structure k is large, there will be little amplification of the horizontal force, and first order analysis will be adequate for the structure. On the other hand, if the value of vertical force tends toward a critical value Vcr (= kh) then displacements and forces in the restraint tend toward infinity. The ratio Vcr/V, which may be expressed as a parameter αcr, is thus an indication of the second order amplification of displacements and forces in the bracing system due to second order effects.
The amplifier is given by:
[1/(1 – 1/αcr)
This amplification factor applies to horizontal forces such as wind loads and imperfection loads.
Criteria for considering second order effects
According to BS EN 1993-1-1, 5.2.1(2), the effects of the deformed geometry of the structure (second order effects) need to be considered if the deformation significantly increase the forces in the structure or if the deformations significantly modify structural behaviour. For elastic global analysis, clause 5.2.1 says that the second order effects are significant if the parameter αcr < 10, where αcr is determined by first order analysis and for a braced frame is defined by the approximate expression:
αcr = (HEd/VEd) x (h/δh,Ed)
where:
HEd is the design value of the horizontal reaction at the bottom of the storey to the horizontal loads and the equivalent horizontal forces1
VEd is the total design vertical force on the structure on the bottom of the storey
δh,Ed is the horizontal displacement at the top of the storey, relative to the bottom of the storey, when the frame is loaded with horizontal loads (e.g. wind) and equivalent horizontal forces which are applied at each floor level
h is the storey height.
Methods for determining second order effects
Where second order effects need to be evaluated, BS EN 1993-1-1, 5.2.2 says that they may be allowed for by:
- An appropriate second-order analysis, taking into account the influence of the deformation of the structure.
- Using appropriate (increased) buckling lengths of members
- Amplification of an elastic first order analysis using the initial geometry of the structure.
Second Order Analysis
A range of second order analysis software is available. Use of any software will give results that are to some extent approximate, depending on the solution method employed, the types of second-order effects considered and the modelling assumptions. Generally, second-order software will automatically allow for frame imperfections, so the designer will not need to calculate and apply the equivalent horizontal forces. The effects of deformed geometry (second-order effects) will be allowed for in the analysis. The effect of member imperfections and such things as residual stresses are allowed for if verifying members in accordance with the rules in Section 6 of BS EN 1993-1-1.
Use of increased column buckling length
The use of increased column buckling effective lengths is generally not recommended, simply because of the manual effort involved in calculating the effective length factors. However, if this option is chosen, effective length factors can be determined using a source of non-conflicting complementary information (NCCI), such as BS 5950 Annex E or DD ENV 1993-1-1 Annex E.
Amplification of first order effects
Use of amplified first order effects is subject to the limitation that αcr ≥ 3 (if αcr is less than 3, second order analysis must be used). The amplifier is given by:
[1/(1 – 1/αcr)
Only the effects due to the horizontal forces (including the equivalent horizontal forces) need to be amplified. In a braced frame, where the beam to column connections are pinned and thus do not contribute to lateral stiffness, the only effects to be amplified are the axial forces in the bracing members and the forces in columns that are due to their function as part of the bracing system.











Good
Efforts
I appreciate it