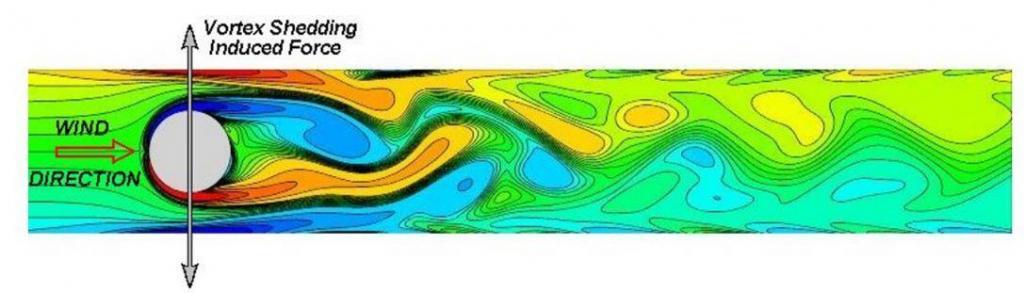
In fluid dynamics, a Kármán vortex street is a repeating pattern of swirling vortices caused by the unsteady separation of flow of a fluid around blunt bodies. When wind blows across a structural member such as tall buildings, vortices are shed alternately from one side to the other. This generates alternating low-pressure zones at the downside of the structure giving rise to a fluctuating force acting at right angles to the wind direction. This phenomenon is referred to as vortex shedding.
When a vortex forms on the side of a building, it creates a suction force. The force generated by an individual vortex is not so large but the potential problem is that vortices tend to form in well-organized patterns and rock the building as they shed alternately from each side. A tall building will generate a Kármán vortex street if it has a uniform shape along its height and is in a steady wind—that is, one with little turbulence. Therefore, for tall buildings that are isolated or very tall, vortex shedding must be accounted for in the design.
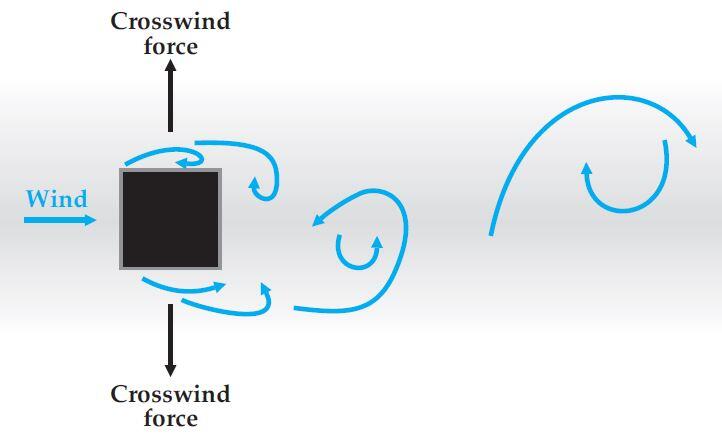
buffeted by steady winds, exert alternating forces on the
structure (black arrows), and, once detached, form a so-called
Kármán street downwind of the building (Irwin, 2010).
In the evaluation of tall buildings against vortex shedding, one needs to ascertain the natural frequency of vibration of the tall building fb, and the frequency with which vortices are shed from the building into the vortex street fv. When these two frequencies are equal, resonance sets in and the building experiences large cross wind oscillations.
A building’s fundamental frequency depends on its structural system and mass distribution, and structural designers of large buildings typically use specialized software to help them accurately compute that frequency (see video example of determination of natural frequency of a multi-storey building using Staad Pro). For a 50-story building, fb is typically about 0.2 Hz, corresponding to a period of 5 seconds. For a 100-story building, fb is in the range of 0.1– 0.125 Hz, corresponding to a period of 8–10 seconds, but some super-tall structures have been conceived for which the frequency is as low as 0.05 Hz, corresponding to a 20-second period (Irwin, 2010).
The frequency of vortex shedding is given by the Strouhal relationship;
fv = SU/w
where;
U is the wind speed,
w is the width of the building that faces the wind, and
S is the Strouhal number, which is often treated as a constant that depends on only the cross-sectional shape of the building.
With this relationship, the critical wind speed at which at which fb = fv can be calculated.
Reducing the effects of vortex shedding
One of the ways of reducing the action caused by vortex shedding is to stiffen the building. This increases the natural frequency of the building, and subsequently increases the critical wind speed at which resonance can occur. However, increasing the stiffness can work in buildings that are not too tall, but for mega tall buildings, other strategies should be adopted to minimise cost.
Another way of reducing the effect of vortex shedding is to interrupt coherent shedding in the building under the effect of wind. One technique is to have the structure’s cross section vary with building height. Then w and S also change with building height, which makes fv a function of height as well. As a result, the wind “becomes confused” and vortices lose their coherence. This was used in the world’s tallest building, Burj Khalifa.

Other effective shaping strategies are softening sharp corners, creating openings in the building for the wind to bleed through, and adding spoilers that break up the vortices much as do the spiral bands, or strakes, seen on many chimney stacks.
A complementary strategy for controlling the response to vortex excitation is to draw the energy out of the building’s crosswind oscillations with special damping systems.
References
(1) Irwin P. A. (2010): Vortices and tall buildings: A recipe for resonance. American Institute of Physics, S-0031-9228-1009-350-6
(2) Giosan, 2005: Vortex shedding induced load on free standing structures. Structural vortex shedding estimation methodology and finite element simulation. Downloaded from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.582.3179&rep=rep1&type=pdf (Assessed on 20th February, 2019)










