Structural Analysis and Design of Residential Buildings Using Staad.Pro, Orion, and Manual Calculations

This should be a long post, but I am going to try and keep it as brief as possible. This post is more like an excerpt from the publication ‘Structural Analysis and Design of Residential Buildings using Staad Pro V8i, CSC Orion, and Manual calculations’. Here, we are going to briefly present some practical analysis and design of some reinforced concrete elements using Staad Pro software, Orion software, and manual calculations. Ultimately, we are going to make some comparisons of the results obtained based on the different methods adopted in the analysis and design. To learn how to model, design, and detail buildings from the scratch using Staad Pro, Orion, and manual methods, see the link at the end of this post.

To show how this is done, simplified architectural floor plans, elevations, and sections, for a residential two-storey building have been shown below for the purpose of structural analysis and design (see the pictures below).

Fig 1: Ground Floor Plan

Fig.2: First Floor Plan

Fig.3: Front View

Fig.4: Back View

Fig.5: Right View

Fig.6: Left View

The first step in the design of buildings is the preparation of the ‘general arrangement’, popularly called the G.A. The G.A. is a drawing that shows the disposition of the structural elements such as the slabs and their types, the floor beams, the columns, and their interaction at the floor level under consideration. For the architectural drawings above, the adopted G.A. is shown in Figure 7. below. There are no spelt out rules about how to prepare G.A. from architectural drawings, but there are basic guidelines that can guide someone on how to prepare a buildable and structurally efficient G.A.

Design data:
F_ck = 25 N/mm², F_yk = 460 N/mm², C_nom (slabs) = 25mm, C_nom (beams and columns) = 35mm, C_nom (foundations) = 50mm
Thickness of slab = 150mm; Dimension of floor beams = 450mm x 230mm; Dimension of columns = (230 x 230mm)

DESIGN OF THE FLOOR SLABS
PANEL 1: MANUAL ANALYSIS

The floor slab (PANEL 1) is spanning in two directions since the ratio (k) of the longer side (Ly) to the shorter side (Lx) is less than 2.
Hence, k = Ly/Lx = 3.825/3.625 = 1.055 (say 1.1)

Moment coefficients (α) for two adjacent edges discontinuous (pick from table);
Short Span
Mid-span = 0.042
Continuous edge = 0.056
Long Span
Mid-span = 0.034
Continuous edge = 0.045

Design of short span
Mid span
M = αnLx² = 0.042 × 10.9575 × 3.6252 = 6.0475 KN.m
M_Ed = 6.0475 KNm
Effective Depth (d) = h – Cc – ϕ/2
Assuming ϕ12mm bars will be employed for the construction
d = 150 – 25 – 6 = 119mm; b = 1000mm (designing per unit width)

k = M_Ed/(f_ckbd² )
= (6.0475 × 10⁶)/(25 × 1000 × 119² ) = 0.0171
Since k < 0.167 No compression reinforcement required
z = d[0.5+ √(0.25 – 0.882k)] = z = d[0.5+ √(0.25 – (0.882 × 0.0273)] = 0.95d
A_s1 = M_Ed/(0.87f_yk z)
A_s1 = (6.0475 × 10⁶)/(0.87 × 460 × 0.95 × 119) = 133.668 mm²/m
Provide Y12mm @ 250mm c/c BOT (A_Sprov = 452 mm²/m)

A little consideration will show that this provided area of steel will satisfy serviceability limit state requirements. To see how to carry out deflections and crack control verifications, see the the link at the bottom of this post.

Result from Orion showing the Short Span (mid span) design moments (Wood and Armer effects inclusive) (PANEL 1)

Result from Staad showing the Short Span (mid span) design moments (Wood and Armer effects inclusive) (PANEL 1)

A little observation will show that the design moment values from the different methods are very similar. The full detailing of the floor slabs is as shown below.

Figure 9: Bottom Reinforcement Detailing

Figure 10: Top Reinforcement Detailing

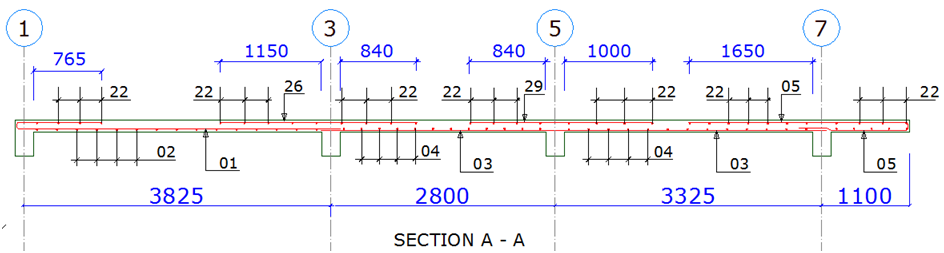
Figure 11: Section of the floor slab

DESIGN OF THE BEAMS
Let us take Beam No 1 from our GA as a design case study:
The loading of the beam has been carried out as shown below. The beam is primarily subjected to load from the slab, the weight of wall, and its own self-weight. To see how to manually calculate the loading on beams, follow the link at the end of the post.

The internal forces from the loading is as shown below;

The internal forces from Orion software for Beam No 1 is as shown below. Load decomposition using finite element analysis was used for the load transfer.

The internal forces from Staad software for Beam No 1 is as shown below.

A_s1 = M_Ed/(0.87f_ykz)
= (36.66 × 10⁶)/(0.87 × 460 × 0.95 × 399) = 241.667 mm²
Provide 2Y16 mm BOT (A_Sprov = 402 mm²)
The detailing of Beam No 1 is as shown below;

DESIGN OF THE COLUMNS
Loads from slabs and beams are transferred to the foundations through the columns. In typical cases, columns are usually rectangular or circular in shape. Normally, they are usually classified as short or slender depending on their slenderness ratio, and this, in turn, influences their mode of failure. Columns are either subjected to axial, uniaxial, or biaxial loads depending on the location and/or loading condition. Eurocode 2 demands that we include the effects of imperfections in the structural design of columns. The design of columns is covered in section 5.8 of EC2.

The column axial loads have been obtained by summing up the reactions from all the beams supported by the columns, including the self weight of the column.

Let us use column A1 as example.

At the roof level, the column is supporting beam No 2 (Support Reaction V₁ = 13.27 KN) and Beam No 3 (Support Reaction V_A = 12.99 KN). At the first floor level (see Analysis and Design of Beam No 1 and 2), the column is supporting Beam No 1 (Support Reaction V₁ = 41.38 KN), and Beam No 2 (Support Reaction V_A = 42.49 KN). Therefore the summation of all these loads gives the axial load transferred from the beams. For intermediate supports, note that the summation of the shear forces at the support gives the total support reaction (neglect the signs and use absolute value. Another method of calculating Column Axial Load is by Tributary Area Method. This method has not been adopted in this work.

COLUMN A1
Total Columns Self weight = 12.14 KN
Load from roof beams = 13.27 + 12.99 = 26.26 KN
Load from floor beams = 46.21 + 42.49 = 88.70 KN
Total = 127.13 KN
 
Axial Load from Orion (A1) = 126.6 KN
Axial Load from Staad (A1) = 130.684 KN

COLUMN A3
Total Columns Self weight = 12.14 KN
Load from roof beams = 35.41 + 11.46 = 46.87 KN
Load from floor beams = 105.33 + 60.85 = 166.18 KN
Total = 225.19 KN

Axial Load from Orion (A3) = 202.3 KN
Axial Load from Staad (A3) = 201.632 KN

COLUMN A5
Total Columns Self weight = 12.14 KN
Load from roof beams = 17.19 + 5.70 = 22.89 KN
Load from floor beams = 83.64 + 37.91 = 121.55 KN
Total = 156.58 KN

Axial Load from Orion (A5) = 155.9 KN
Axial Load from Staad (A5) = 163.207 KN

COLUMN A7
Total Columns Self weight = 12.14 KN
Load from roof beams = 43.15 + 9.48 = 52.63 KN
Load from floor beams = 38.26 + 62.45 = 100.71 KN
Total = 165.48 KN

Axial Load from Orion (A7) = 133.9 KN
Axial Load from Staad (A7) = 140.392 KN

As you can see, for design purposes, the axial loads from the three methods are very comparable. To see how to obtain the column design moments from the use of sub-frames, follow the link at the end of the post.

Design of Column E5
Reading from chart; d₂/h = 0.2;
M_Ed/(f_ck bh² )
= (10.002 × 10⁶)/(25 × 230 × 230² ) = 0.03288
N_Ed/(f_ckbh)
= (399.88 × 10³)/(25 ×230 × 230) = 0.302
From the chart:
(A_sF_yk)/(bhf_ck ) = 0.05
Area of longitudinal steel required (As) = (0.05 × 25 × 230 × 230)/460 = 143.75 mm²
A_s,min = 0.10 NEd/fyd
= (0.1 × 399.887)/400 = 0.099 mm² < 0.002 × 230 × 230 = 105.8 mm²
Provide 4Y16mm (Asprov = 804 mm²)

Links
Minimum size = 0.25ϕ = 0.25 × 16 = 4mm < 6mm
We are adopting Y8mm as links
Spacing adopted = 200mm less than min{b, h, 20ϕ, 400mm}

Result from Orion for column E5

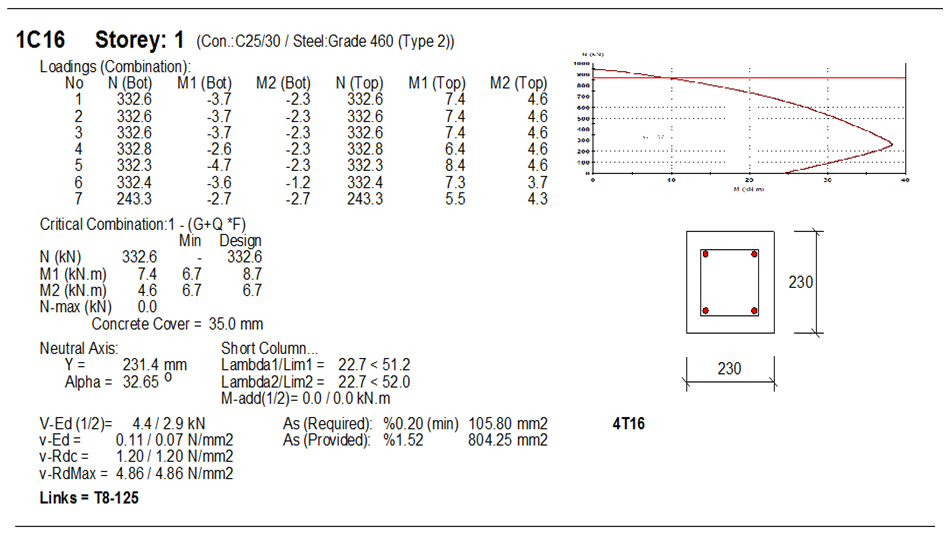
Result from Staad for column E5

Staad Provided Y8@225mm links
The column detailing is as shown below;

DESIGN OF FOUNDATIONS
All loads from the superstructure of a building are transferred to the ground. If the foundation of a building is poorly designed, then all the efforts input in designing the superstructure is in vain. It is therefore imperative that adequate care is taken in the design of foundations. Foundation design starts with a detailed field and soil investigation. It is very important to know the index and geotechnical properties of the soil, including the soil chemistry, so that the performance of the foundation can be guaranteed.

Analysis and Design of footing E8

Bearing Capacity of the foundation = 150 KN/m²;

Effective depth
Concrete cover = 50mm
AssumingY12mm bars,
d = 400 – 50 – 6 = 344mm
The ultimate limit state design moment can be obtained by considering the figure below;

k = M_Ed/(f_ck bd²)
= (37.518 × 10⁶)/(25 × 1000 × 344² ) = 0.01268 (designing per metre strip)
Since k < 0.167 No compression reinforcement required
z = d[0.5+ √(0.25 – 0.882k)] = z = d[0.5+ √(0.25 – (0.882 × 0.0273)] = 0.95d
A_s1 = M_Ed/(0.87f_ykz)
= (37.518 × 10⁶)/(0.87 × 460 × 0.95 × 344) = 286.869 mm²/m

To calculate the minimum area of steel required;
f_ctm = 0.3 × (f_ck)^(2⁄3) = 0.3 × 25 ^(2⁄3) = 2.5649 N/mm² (Table 3.1 EC2)
A_Smin = 0.26 × f_ctm/F_yk × b × d = 0.26 × 2.5649/460 ×1000 × 344 = 498.7 mm²
Check if A_Smin < 0.0013 × b × d (447.2 mm²)
Since, A_Smin = 498.7 mm², the provided reinforcement is adequate.
Provide Y12 @ 200mm c/c (A_Sprov = 565 mm²/m) each way

Shear at the column face
Ultimate Load on footing from column = 399.887 kN
Design shear stress at the column perimeter v_Ed = βV_Ed/(u₀d)
β is the eccentricity factor (see section 6.4.3 of EC2)
β = 1+ 1.8√[(16.48/230)²+(8.99/230)²] = 1.146
Where u_o is the column perimeter and d is the effective depth
v_Ed = βV_Ed/(u₀d)
= (1.15 × 399.887 × 10³)/(4(230) × 344) = 1.452N/mm²
V_Rd,max = 0.5vf_cd
v = 0.6[1 – (f_ck/250) ] = 0.6[1 – (25/250) ] = 0.54 N/mm²
f_cd = (α_cc f_ck)/γ_c = (0.85 × 25)/1.5 = 14.167 N/mm²
V_Rd,max = 0.5 × 0.54 × 14.167 = 3.825 N/mm²v_Ed < V_Rd,max. This is very ok

Transverse shear at ‘d’ from the face of column

Width of shaded area = a – d = 0.635 – 0.344 = 0.291m
Area of shaded area = (1.5m × 0.291m) = 0.4365 m²
Therefore, ΔV_Ed = (189.386 + 175.939)/2 × 0.4365 m² = 79.077 KN
v_Ed = V_Ed/bd = (79.077 × 10³)/(1500 × 344) = 0.15325 N/mm²
V_Rd,c = [C_Rd,c k (100ρ₁ f_ck )^(1/3) + k¹.σ^cp] × (2d/a) ≥ (V_min + k₁.σ,sub>cp) bw.d
C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12
k = 1 + √(200/d) = 1+√(200/344) = 1.7624 > 2.0, therefore, k = 1.7624
V_min = 0.035k^(3/2) f_ck^(1/2)
V_min = 0.035 × (1.7624)^(3/2) × (25)^(1/2) = 0.4094 N/mm²
ρ₁ = As/bd = 565/(1000 × 344) = 0.001642 < 0.02;
V_Rd,c = [0.12 × 1.7624 (100 × 0.001642 ×25 )^(1/3) ] = 0.3386 N/mm² × (2d/a) < V_min
But in this case, d = a
Hence, V_Rd,c = 2 × 0.3386 = 0.6772 N/mm²
Since V_Rd,c (0.6772) > V_Ed (0.1503 KN), No shear reinforcement is required.

Punching Shear at 2d from the face of column
Punching shear lies outside the footing dimensions. No further check required.

Design Result from Orion

The detailing of the footing is as shown below;

The structural analysis and design of all members have been fully done, including a step by step tutorial on how to model and design on Orion and Staad Pro, and how to manually design. See the completed models below;

To download the simplified e-book where all the members have been designed and completely detailed, including bar bending schedule and quantification of materials, click HERE.

Thank you, and God bless you.