Design of Helical Staircase

Helical staircases provide alternatives for vertical circulation in buildings. Due to their curved and elegant nature, they inspire awe and admiration whenever they are properly designed and constructed. The analysis and design of a helical staircase can be complex due to an inherent interaction of vertical moments, horizontal moments, vertical shear, lateral shear, axial force, and torsion. The complexity of helical staircases is due to their geometry.

Geometrically, a helical surface is a three-dimensional structure in space consisting of a warped surface that is generated by moving a straight line touching a helix so that the moving line is always perpendicular to the axis of the helix. In an oblique helix, the generating line always maintains a fixed angle with the helix. Since a helical staircase is a space member, all the six internal actions come into play at any section, having varying directions and lines of actions.

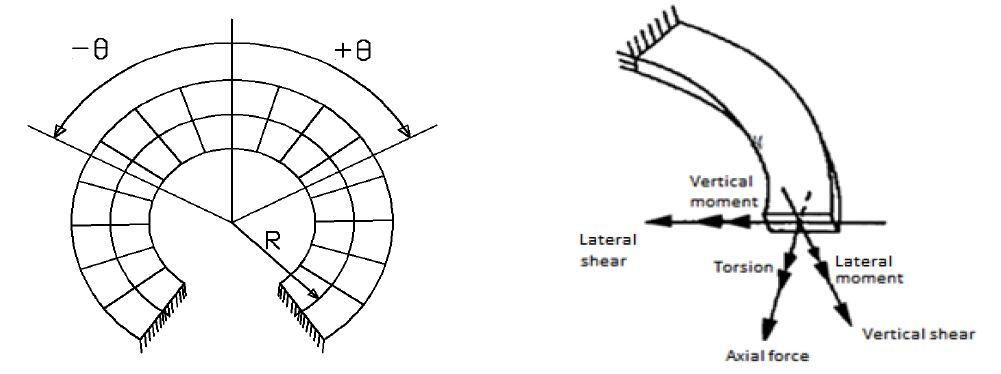
Despite the existence of the six internal stresses at any section in a helical staircase, they are usually designed for the horizontal bending moment only. Furthermore, helical staircases can sometimes be idealised as a fixed ended curved beam for the purposes of design due to their complexity.

Bergman (1956) proposed an approximate solution to helical staircases called the in-plane beam solution. The method reduces the problem to that of a horizontal bow girder, which fails to take into account the inherent structural strength of a helical beam.

Morgan (1960) and Scordelis (1960) presented the analysis of the longitudinal elastic axis of the helical beam as a three-dimensional structure indeterminate to the sixth degree. By selecting the redundant at mid-span and using the principle of symmetry, all but two of the redundants become zero. The two redundants at mid-span are the horizontal shear H and the vertical moment M_o.

Cusens and Trirojna (1964) carried out a test on half scaled fixed ended helical staircase and confirmed the equilibrium equations derived by Morgan. Santathadaporn and Cusens (1966) worked further on helicoidal stair slabs to simplify the design process. They proposed some simple equations for design purpose with the provision of using coefficients in the equations. They used computer program to solve those complicated equations and constructed a series of design charts to provide the values of the coefficients.

Reynolds and Steedman (1988) attempted further modifications of the charts provided by Santathadaporn and Cusens. The analytical approach they chose was the one made by Morgan and Scordelis. The proopsed equations and coefficients for determination of the internal stresses are as follows;

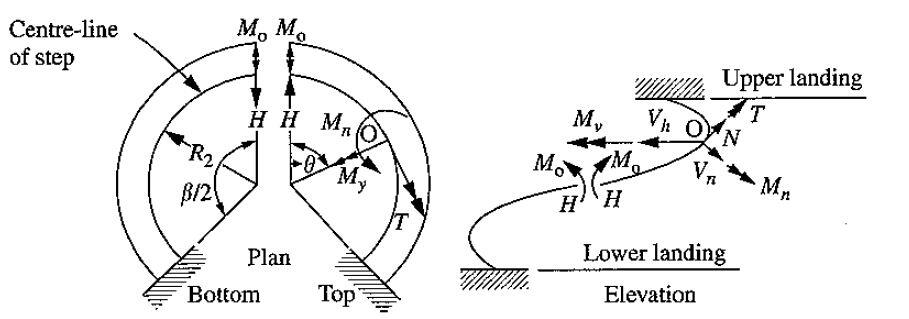
Horizontal moment M_n = M_o sinθsinϕ – HR₂θtanϕcosθsinϕ – HR₂sinθcosϕ + nR₁sinϕ(R₁sinθ – R₂θ) —— (1)

Vertical moment M_y = M_ocosθ + HR₂θtanϕsinθ – nR₁²(1 – cosθ) —— (2)

Torsion T = (M_osinθ – HR₂θcosθtanϕ + nR₁²sinθ – nR₁R₂θ)cosϕ + HR₂sinθsinϕ —— (3)

Axial force N = -Hsinθcosϕ – nR₁θsinϕ —— (4)

Vertical shear V_n = nR₁θcosϕ – Hsinθsinϕ —— (5)

Radial horizontal shear V_h = Hcosθ —— (6)

Where;
M_o = Redundant moment acting tangentially at the midspan = k₁nR₂²
H = Horizontal redundant force at midspan = k₂nR₂
M_vs = Vertical moment at supports= k₃nR₂²
n = total design load on the staircase (kN/m²)
R₁ = Radius of centreline of loading = 2(R_o³ – R_i³)/3(R_o² – R_i²)
R₂ = Radius of centreline of steps = 0.5(R_i + R_o)
θ = angle subtended in plan between point considered and mid-point of stair
ϕ = slope of tangent to helix centreline measured from horizontal
β = Total angle formed by the helical staircase in plan
k₁ = GC/EI₁
k₂ = GC/EI₂
I₁, I₂ = Second moment of area of stair section about horizontal axis and axis normal to slope respectively.

The 36 design charts presented by Santathadaporn and Cusens (1966) covered ranges of β of 60° to 720°, ϕ of 20° to 50°, b/h of 0.5 to 16 and R₁/R₂ of 1.0 to 1.1, based on a ratio of G/E of 3/7.

Four design charts are provided in Table 177 of (Reynolds and Steedman 10th Edition) and (Tables 2.90 and 2.91 of 11th Edition) for a ratio of G/E of 0.4 and by taking C to be one-half of the St. Venant value for plain concrete. These charts cover ranges of β of 30° to 360° and ϕ of 20° to 40°, with values of b/h of 5 and 10 and R₁/R₂ of 1.0 and 1.1, these being the ranges most frequently met in helical stair design. According to Reynolds and Steedman (1988), interpolation between the various curves and charts on the Tables will be sufficiently accurate for preliminary design purposes.

According to a 2015 research from the Department of Civil Engineering, Addis Ababa University, Ethiopia, the solution provided in Reynolds and Steedman is the best so far, even though it has its limitations. The charts presented in the book give good information about internal actions but only qualitatively, and indicate set of constants to put in his equations then solved. And, as Reynolds himself stated in his book, his results are only satisfactory for preliminary analysis only as lots of interpolation is involved.

Design Example

Design a helicoidal stair having an angle of inclination ϕ of 25° to the horizontal plane to support a uniform imposed load of 3 kN/m². The stair is to have a width of 1.5 m and the minimum thickness of the waist is 150 mm, the radius to the inside of the stair R_i is 1000 mm, and the angle β turned through by the stair is 180°. (Weight of finishes = 1.2 kN/m²; weight of riser/thread = 1.875 kN/m²)

Solution
Permanent actions;
Self-weight of waist (150 mm thick) = 0.15 × 25 = 3.75 kN/m²
Weight of stepped area = 1.875 kN/m²
Weight of finishes = 1.2 kN/m²
Total dead load (characteristic permanent action) g_k = 6.825 kN/m²

Variable action(s);
Characteristic variable action on staircase q_k = 3 kN/m²

At ultimate limit state E_d = 1.35g_k + 1.5q_k = 1.35(6.825) + 1.5(3) = 13.71 kN/m²

Geometry
Inner radius R_i = 1000 mm = 1 m
Outer radius R_o = R_i + b = 1000 + 1500 = 2500 mm = 2.5 m

The radius of the centreline of the load R₁ is;
R₁ = 2(R_o³ – R_i³)/3(R_o² – R_i²) = 2(2.5³ – 1.0³)/3(2.5² – 1.0²) = 1.857 m
R₂ = 0.5(R_i + R_o) = 0.5(1000 + 2500) = 1750 mm = 1.75 m

R₁/R₂ = 1.857/1.75 = 1.06
b/h = 1500/150 = 10
β = 180°; ϕ = 25°

Reading from chart (Tables 177 of Reynolds and Steedman, 2005);

(b/h = 10; R₁/R₂ = 1.0; β = 180°; ϕ = 25°) k₁ = -0.02; k₂ = +1.21; k₃ = -0.1
(b/h = 10; R₁/R₂ = 1.1; β = 180°; ϕ = 25°) k₁ = -0.09; k₂ = +1.45; k₃ = -0.19

Interpolating between R₁/R₂ = 1.0 and 1.1, we obtain;
k₁ = -0.062; k₂ = +1.354; k₃ = -0.154

Structural Analysis
M_o = Redundant moment acting tangentially at the midspan = k₁nR₂² = -0.062 × 13.71 × 1.75² × 1.5 = -3.905 kNm
H = Horizontal redundant force at midspan = k₂nR₂ = 1.354 × 13.71 × 1.75 × 1.5 = 48.728 kN
M_vs = Vertical moment at supports = k₃nR₂² = -0.154 × 13.71 × 1.75² × 1.5 = -9.698 kNm

The values of M_o and H can now be substituted into equations (1) to (6) to obtain the internal stresses along the staircase.

For instance, when θ = 60°
n (as uniformly distributed load in kN/m) = 13.71 x 1.5 = 20.565 kN/m

Vertical moment M_y,_Ed = M_ocosθ + HR₂θtanϕsinθ – nR₁²(1 – cosθ) = -3.905cos60 + (48.729 × 1.75 × (π60/180) × tan25 × sin60) – 20.565 × 1.875² × (1 – cos60) = -1.9525 + 36.055 – 36.149 = -2.046 kNm

Horizontal moment M_n,_Ed = M_o sinθsinϕ – HR₂θtanϕcosθsinϕ – HR₂sinθcosϕ + nR₁sinϕ(R₁sinθ – R₂θ) = (-3.905 × sin60 × sin25) – [48.728 × 1.75 × (π60/180) × tan25 × cos60 × sin25] – (48.728 × 1.75 × sin60 × cos25) + [20.565 × 1.875sin25(1.875sin25 – 1.75(π60/180)] = -1.429 – 8.797 – 66.930 – 16.945 = -94.101 kNm

Torsion T = (M_osinθ – HR₂θcosθtanϕ + nR₁²sinθ – nR₁R₂θ)cosϕ + HR₂sinθsinϕ = [-3.905sin60 – (48.728 × 1.75 × (π60/180) × tan25 × cos60) + (20.565 × 1.875² × sin 60) – (20.565 × 1.875 × 1.75 × (π60/180))]cos25 + (48.728 × 1.75 × sin60 × sin25) = -23.085 + 31.210 = 8.125 kNm

Axial force N = -Hsinθcosϕ – nR₁θsinϕ = [-48.728 × sin60 × cos 25] – [20.565 × 1.857 × (π60/180) × sin25] = -38.245 – 16.898 = -55.143 kN

Vertical shear V_n = nR₁θcosϕ – Hsinθsinϕ = [20.565 × 1.857 × (π60/180) × cos25] – [-48.728 × sin60 × sin 25] = 36.238 + 17.834 = 54.072 kN

Radial horizontal shear V_h = Hcosθ = -48.728 × cos60 = -24.364 kN

The calculation should be carried out for different angles, and the maximum values used for the structural design.

To request for this article or any other Structville article in PDF format, click HERE (premium but very affordable).

References
[1] Bergman V.R. (1956): Helicoidal staircases of reinforced concrete, A.C.I. Journal Proceedings 53(4):403‐412
[2] Cusens A.R., Trirojna S. (1964): Helicoidal Staircase Study. ACI Journal, Proceedings, 61(1):85‐101.[2]
[3] Morgan V.A. (1960): Comparison of Analysis of Helical Staircases. Concrete and Construction Engineering, (London) 55(3):127‐132.
[4] Reynolds C.E., Steedman J.C. (1988): Reinforced Concrete Designers Handbook, Tenth Edition, E & FN Spon Ltd, London
[5] Santathadaporn, S. and Cusens, A R. (1966): Charts for the Design of Helical Stairs with Fixed Supports. Concrete and Construction Engineering, 61(2):46-54.
[6] Scordelis A. C. (1960): Closure to Discussion of Internal Forces in Uniformly Loaded Helicoidal Girder. ACI Journal Proceedings, 56(6):1491‐1502.