The 2225 mm x 2225 mm pad footing shown above is meant to support a 230 x 230 mm column from the superstructure of a building. The characteristic dead and imposed loads on the column are 600 kN and 210 kN respectively, excluding the weight of the column stub. Making use of your personal engineering judgment, kindly answer the following questions using the information provided;
(1) Will you accept the size of the pad footing provided if the verified allowable bearing capacity of the soil is 175 kN/m2?
(2) What is your calculated value of the total service load for determining the footing dimensions?
(3) What informed your decision? Did you make any assumptions?

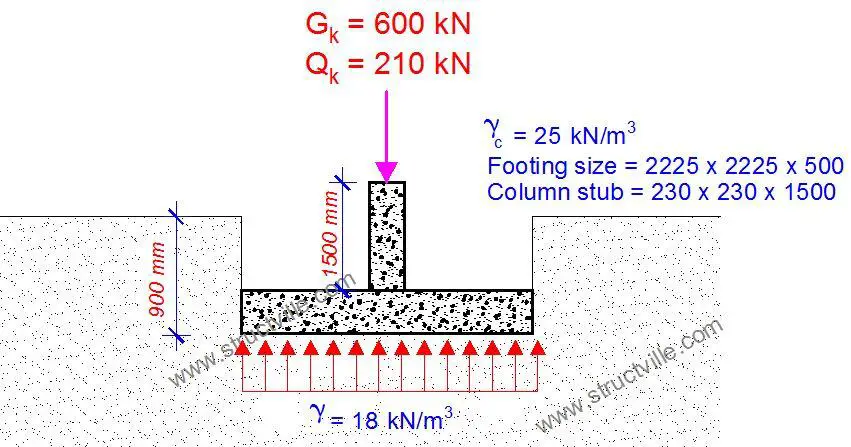


Load from column = 600+210kN
Self weight of column = (0.23*0.23*1.5*25)=1.98kN
Self weight of footing = (2.25*2.25*0.5*25)=63.28kN
Weigh of soil above footing = ((2.25*2.25)-(0.23*0.23))*(0.9-0.5)*18= 36kN
Total load = 600+210+1.98+63.28+36=911.26kN
Minimum Area required = 911.26/175 = 5.21sq.m
Area provided = (2.25*2.25)= 5.06sq.m
In Den ark, we have two scenario’s to look at. 1. With G multiplied with 1,2 and no Q. The se ond scenario is G+1,5Q and we normallu use Concretes load at 24 kN/m3.
This gives instead.
1st scenario 600 * 1,2 + 1,90 + 60,74 + 36 = 1006 kN which is a load under structure on 198,9 kN/m2
2nd scenario 600+210*1,5+1,90+60,74+36 = 1013,6 kN (a little bit higher) which gives the result under the plate 200,2 kN/m2 it should have been abouy 2,45 x 2,45 and the plate should been reinforced so it kan mange to move the load out to the whole plantes area. Also check the plate for pulling the column thru the plate.
Weight of the stub:
25*0.23*0.23*1.5= 1.98kn
Total dead load = 1.98+600= 601.98kn
Determine area require to carry the service load of (601.98+210= 811.98kn);
Bearing capacity= service load/area.
Area =811.98/175= 4.64m^2
L=B= 2.15m, this means that the length and with of the footing is sufficient.
For the depth:
0.5v=N/(cp*d)
When v is lesser of 0.8*fcu^1/2 or 5n/mm^2
Assume that compressive strength of the concrete is 25n/mm^2
0.8*25^1/2= 4, hence for is used.
Cp; column perimeter= 0.23*4= 0.92m
Ultimate load = 1.4gk+1.6qk= (1.4*601.98)+(1 6*210)= 1178. 8kn
Effective depth(d)= 1178.8/0.92*4=320.3d
To tall depth = d+cover +@/2=
320.3+50+12/2= 376.3m. Hence, the provision is safe and acceptable.
(ii) Calculated service load is 811.98
2.225×2.225×0.500 = 2.48m3
Dead weight = 2.48 × 25 = 62kN
Column stub = 0.230×0.230×1.500×25 = 2.0kN
Total dead load = 2+62+ 600 =664kN
Total variable load = 210kN
EC7 factors for design approach 1
Yg =1.35
Yq= 1.5
Characteristic load. = 1.35 ×664 +210×1.5
= 1211.4kN
Pressure under foundation = 1211.4÷ 4.95
= 245 kPa
Bearing capacity is 175kPa < 245kPa
1.0. Increase the size of foundation. The given size is not adequate.
2.0. 664kN + 210 kN= 874kN
3.0. Size of foundation required. = 1211.4 ÷175 = 6.92m2
use a footing size of 2.70m× 2.70m
Check the settlement also.
Complete the calculations for DA1C2 also.
I support Shubham’s answer assuming backfill to existing ground level. What’s your correct answer?
You guys should look at the relation between the pad depth and its length and width.
It is a “flexible pad” as the pad cantilevers 1 metre to either side of the column stub and its depth is only 0.5 metres.
As a result, it will hardly be able to mobilise a 175kPa reaction at the ends of the pad.
As a pre-sizing rule of thumb hiphothesis, I would assume that the load distributes at a 45º degree angle from the column stub face, giving an overall net distributed area of 1.23×1.23. This area times 175kPa results in 265kN which is not enough to bear the stud load.
A finer calculation could be done by modelling springs and assessing the interaction between the pad and soil rigidities.
But, overall and at first sight, my approach would increase the pad depth.
since foundation footing is designed using service load 1.0gk + 1.0qk
then, 1.0(600) + 1.0(210) = 810kN
footing area = Load/bearing capacity
A=810/175 = 4.628mm²
therefore the size provided is sufficient for serviceability 2.225 X 2.225
you start considering the self weight when you wan to design for ultimate limit state (shear, bending…)