Design of Reinforced Concrete (R.C.) Staircase | Eurocode 2

In multi-storey buildings, ramps, elevators, escalators, and stairs are often used to facilitate vertical circulation. Circulation refers to the movement of people and goods between interior spaces in buildings, and to entrances and exits. Stairs are important building elements that are used to provide vertical circulation and access across different floor levels in a building. It is also recommended that when an access height exceeds 600mm, a staircase should be provided. A staircase can be made of reinforced concrete, steel, timber, and other composite construction materials.

In modern architecture, stairs are designed to be aesthetically pleasing, and they contribute immensely to the interior beauty of a building. There are different types of stairs with different configurations. For stairs in a building, the recommended slope for comfort is 27°, but for practical purposes, this can sometimes be extended to 35°.

Types of staircase

Generally, stairs are usually of the following types:

• straight flight staircase
• circular staircase
• helical staircase
• spiral staircase, or
• a combination of the above-mentioned types.

Straight stairs are stairs along which there is no curvature or change in direction on any flight between two successive floors or levels. There are several possible arrangements of straight stairs. For example, they may be arranged in a straight run with a single flight between floors, or a series of flights without a change in direction.

Also, straight stairs may permit a change in direction at an immediate landing. When the stairs require a complete reversal of direction, they are called parallel stairs or half-landing stairs (turning through 180°). When successive flights are at an angle to each other, (usually 90°), they are called angle stairs or quarter-turn stairs. In addition, straight stairs may be classified as scissors stairs when they comprise a pair of straight runs in opposite directions and are placed on opposite sides of a wall.

Circular stairs when viewed from above appear to follow a circle with a single centre of curvature and large radius.

Curved stairs when viewed from above appear to follow a curve with two or more centres of curvature, such as an ellipse.

The picture below shows a helical staircase.

Spiral stairs are similar to circular stairs except that the radius of curvature is small and the stairs may be supported by a column.

Terminologies in staircase design

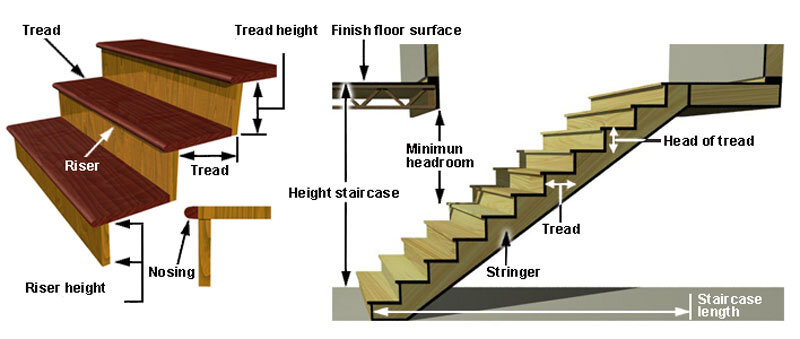
Flight: A series of steps extending from floor to floor, or from a floor to an intermediate landing or platform.

Guard: Protective vertical barrier along edges of stairways, balconies, and floor openings.

Landings (platforms): Used where turns are necessary or to break up long climbs. Landings should be level, as wide as the stairs, and at least 1000mm long in the direction of travel.

Step: Combination of a riser and the tread immediately above.

Rise: Distance from floor to floor.

Run: Total length of stairs in a horizontal plane, including landings.

Riser: Vertical face of a step. Its height is generally taken as the vertical distance between treads.

Tread: Horizontal face of a step. Its width is usually taken as the horizontal distance between risers.

Nosing: Projection of a tread beyond the riser below.

Soffit: Underside of a stair.

Railing: Framework or enclosure supporting a handrail and serving as a safety barrier.

Baluster: Vertical member supporting the handrail in a railing.

Balustrade: A railing composed of balusters capped by a handrail.

Handrail: Protective bar placed at a convenient distance above the stairs for a handhold.

Ideas on the selection of staircase dimensions

Headroom
Ample headroom should be provided not only to prevent tall people from injuring their heads but to give a feeling of spaciousness. A person of average height should be able to extend his hand forward and upward without touching the ceiling above the stairs. The minimum vertical distance from the nosing of a tread to overhead construction should preferably never be less than 2100 mm.

Stairway Width
The width of a stairway depends on its purpose and the number of persons to be accommodated in peak hours or emergencies. Also, there are building codes that regulate the geometric design of stairways. The following can be used as guidelines;

• For residential flats between two to four storeys, use a minimum width of 900 mm, for flats more than 4 storeys, use a width of 1000 mm.
• For public buildings of under 200 persons per floor, use a width of 1000 mm, for buildings between 200 – 400 persons per floor, use a width of 1500 mm. For over 400 persons, use a width between 1500 – 3000 mm. However, when the width of a stairway exceeds 1800 mm, it is necessary to divide it using handrails.

Step Sizes
Risers and treads generally are proportioned for comfort and to meet accessibility standards for the handicapped, although sometimes space considerations control or the desire to achieve a monumental effect, particularly for outside stairs of public buildings. Treads should be at least 250 mm, exclusive of nosing.

The most comfortable height of riser is 175 mm. Risers less than 100 mm and more than 200 mm high should not be used. The steeper the slope of the stairs, the greater the ratio of the riser to tread. In the design of stairs, account should be taken of the fact that there is always one less tread than riser per flight of stairs. No flight of stairs should contain less than three risers.

Structural design of a staircase

The theoretical procedures employed in the structural analysis of stairs is the concept of an idealised line structure and when detailing the reinforcement for the resulting stairs, additional bars should be included to limit the formation of cracks at the points of high-stress concentration that inevitably occur. Typical detailing of corners (edge between flight and landing) of a staircase is shown below;

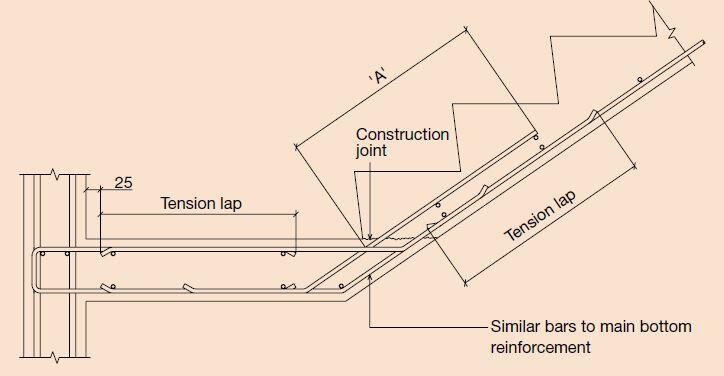
The ‘three-dimensional’ nature of the actual structure and the stiffening effect of the triangular tread areas, both of which are usually ignored when analysing the structure, will result in actual stress distributions that differ from those calculated, and this must be remembered when detailing (Reynolds et al, 2008). The typical nature of internal stresses induced in a simply supported straight flight stair and reinforcement pattern is as shown in the picture below.

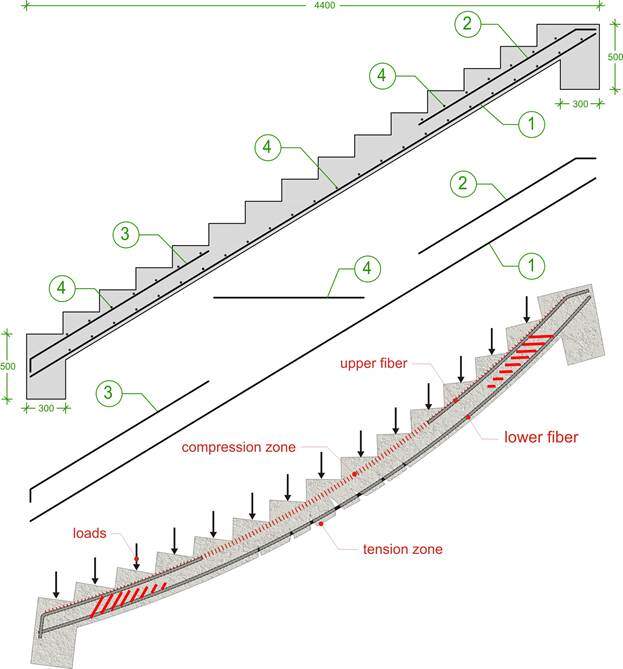
Simple straight flights of stairs can span either transversely (i.e. across the flight) or longitudinally (i.e.along the flight). When spanning transversely, supports must be provided on both sides of the flight by either walls or stringer beams. In this case, the waist or thinnest part of the stair construction need be no more than 60 mm thick say, the effective lever arm for resisting the bending moment being about half of the maximum thickness from the nose to the soffit, measured at right angles to the soffit. When the stair spans longitudinally, deflection considerations can determine the waist thickness.

In principle, the design requirements for beams and slabs apply also to staircases, but designers cannot be expected to determine the deflections likely to occur in the more complex stair types. BS 8110 deals only with simple types and allows a modified span/effective depth ratio to be used. The bending moments should be calculated from the ultimate load due to the total weight of the stairs and imposed load, measured on plan, combined with the horizontal span. Stresses produced by the longitudinal thrust are small and generally neglected in the design of simple systems.

Sample design of reinforced concrete staircase

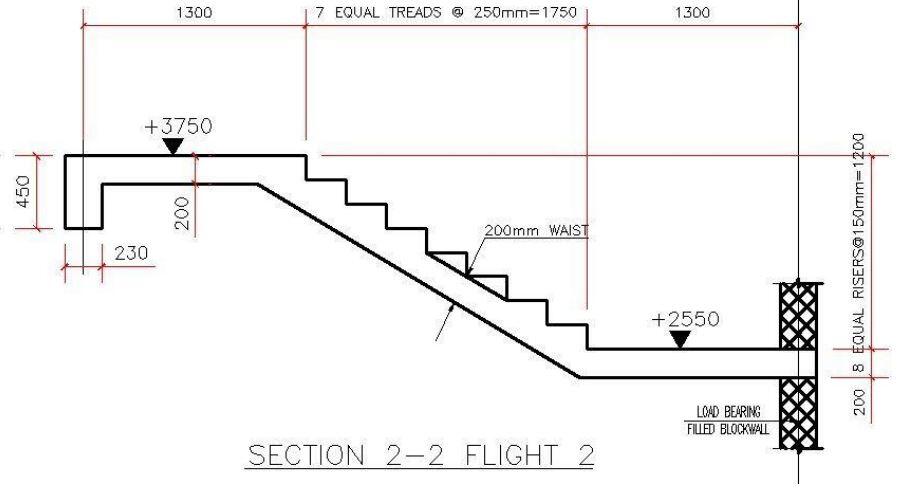
A section of a staircase is shown above. The width of the staircase is 1160mm. We are expected to carry out a full structural analysis and design of the staircase according to EC2 using the following data; Density of concrete = 25 kN/m³; Compressive strength of concrete (f_ck) = 30 N/mm²; Yield strength of steel (f_yk) = 460 N/mm²; Concrete cover = 25mm; Imposed load on staircase (q_k) = 4 kN/m² (category C3).

The structural idealisation of the staircase is shown below;

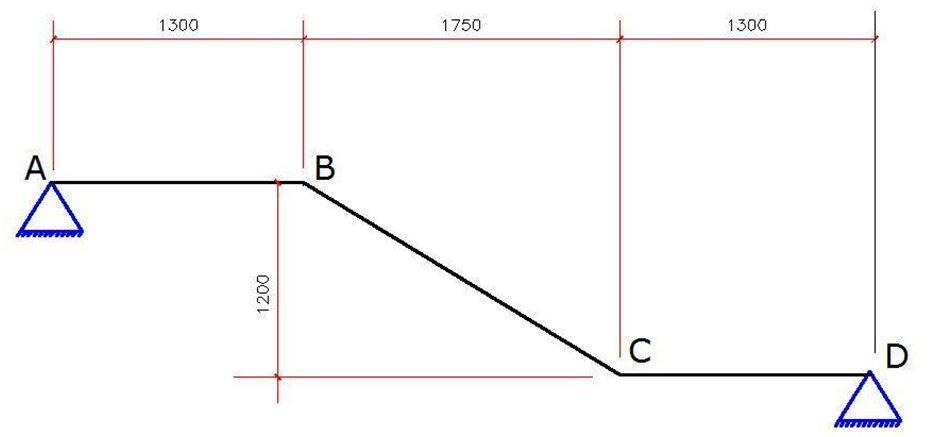
Loading of the staircase

Thickness of waist and landing = 200 mm
Depth of riser = 150mm
Load actions on the stairs
Concrete self weight (waist area) = 0.2 × 25 = 5 kN/m² (normal to the inclination)
Stepped area = 0.5 × 0.15 × 25 = 1.875 kN/m² (global vertical direction)
Finishes (say) = 1.2 kN/m²

We intend to apply all gravity loads purely in the global y-direction, therefore we convert the load at the waist of the stair from local to global direction by considering the angle of inclination of the flight area to the horizontal;

? = tan⁻¹(1.2/1.75) = 34.438989°

Therefore the UDL from waist of the stair in the global direction is given by = (5 × cos 34.438989) = 4.124 kN/m²

Total dead load on flight area (g_k) = 4.124 + 1.875 + 1.2 = 7.199 kN/m
Variable load on staircase (q_k) = 4 kN/m²
The load on the flight area at ultimate limit state = 1.35g_k + 1.5q_k
E_d = 1.35(7.199) + 1.5(4) = 15.719 kN/m²

On the landing;
g_k = 5 + 1.2 = 6.2 kN/m²; q_k = 4 kN/m²

The load on the landing at ultimate limit state = 1.35g_k + 1.5q_k
n = 1.35(6.2) + 1.5(4) = 14.370 kN/m²

The loading of the structure for dead and live loads at ultimate limit state is shown below;

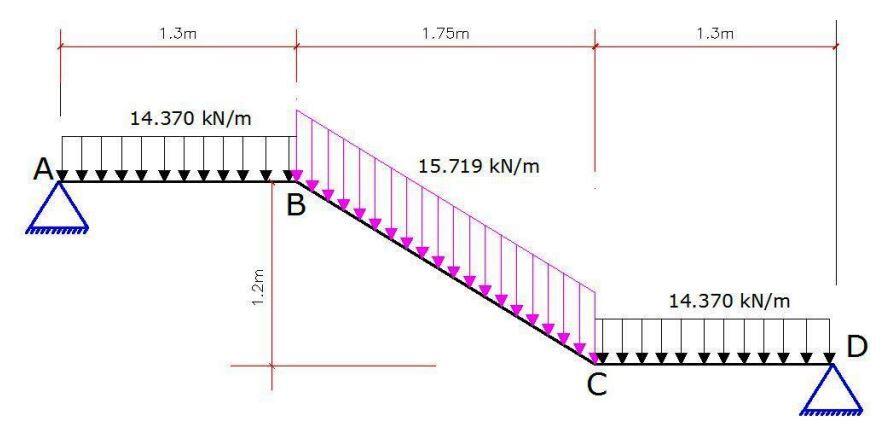
The ultimate bending bending moment diagram due to ultimate loads is shown below; 

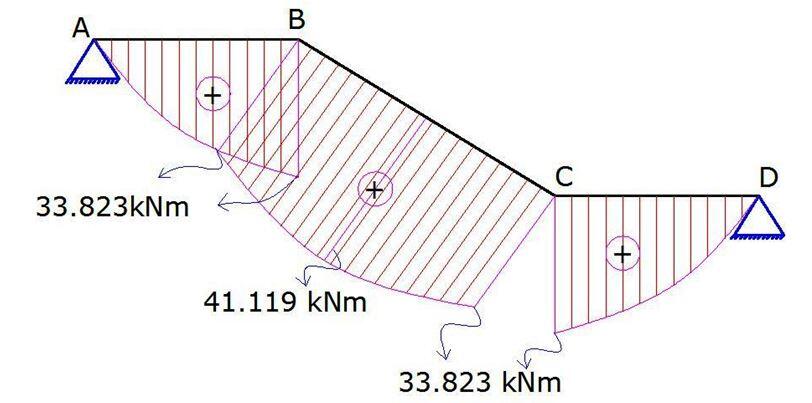
The ultimate shear force diagram is shown below; 

Flexural design of the staircase span 

A little consideration will show that it is best to use the design moment M_Ed = 41.119 kNm to design the entire stairs.

M_Ed = 41.119 kNm
d = h – Cc – ϕ/2
Assuming ϕ12mm bars will be used for the construction
d = 200 – 25 – 6 = 169mm; b = 1000mm (designing per unit width)

k = M_Ed/(f_ckbd²) = (41.119 × 10⁶)/(30 × 1000 × 169²) = 0.0479

Since k < 0.167 No compression reinforcement required
z = d[0.5+ √((0.25 – 0.882k)] = z = d[0.5+ √(0.25 – 0.882 × 0.0479)] = 0.95d

A_s1 = M_Ed/(0.87f_ykz) = (41.119 × 10⁶)/(0.87 × 460 × 0.95 × 169) = 639.96 mm²/m

Provide Y12mm @ 150mm c/c BOT (A_s,prov = 753 mm²/m)

To calculate the minimum area of steel required;
fctm = 0.3 × f_ck^(2⁄3) = 0.3 × 30^2⁄3 = 2.896 N/mm² (Table 3.1 EC2)

A_s,min = 0.26 × f_ctm/f_yk × b × d = 0.26 × 2.896/460 ×1000 ×169 = 276.631 mm²/m
Check if A_s,min < 0.0013 × b × d (219.7 mm²/m)
Since, A_s,min = 276.631 mm², the provided reinforcement is adequate.

Check for deflection 

k = 1.0 for simply supported beams and slab
ρ = As/bd = 753/(1000 × 169) = 0.004455 < 10^-3√30

Since ρ < ρ₀
L/d = k [11 + 1.5√(f_ck) ρ₀/ρ + 3.2√(f_ck) (ρ₀/ρ – 1)^1.5]

L/d = 1.0 [11 + 1.5√30 × (0.005477/0.004455) + 3.2√30 (0.005477/0.004455 – 1)^1.5] = 1.0 (21.1 + 1.9258) = 23.0258

Modification factor β_s = 310/σ_s
σ_s = (310_fykA_s,req)/(500A_s,prov) = (310 × 460 × 639.96)/(500 × 753) = 242.358 N/mm²

β_s = 310/242.358 = 1.2789
Taking the distance between supports as the effective span, L = 4.35m
The allowable span/depth ratio = β_s × 23.0258 = 1.2789 × 23.0358 = 29.460
Actual deflection L/d = 4350/169 = 25.739
Since 25.739 < 29.460, deflection is ok.

Shear design 

Ultimate shear force V_Ed = 35.358 kN
v = V_Ed/bd = (35.358 × 1000)/(1000 × 169) = 0.209 N/mm²
V_Rd,c = [C_Rd,ck(100ρ₁f_ck)^1/3] ≥ (_Vmin)

C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12

k = 1 + √(200/d) = 1 + √(200/169) = 2.087 > 2.0, therefore, k = 2

V_min = 0.035k^1.5f_ck^0.5
V_min = 0.035 × 2^1.5 × 30^0.5 = 0.5422 N/mm²

ρ₁ = As/bd = 753/(1000 × 169) = 0.0044556 < 0.02

V_Rd,c = [0.12 × 2(100 × 0.0044556 × 30)^1/3] = 0.569 N.mm²
Since V_Rd,c > V_Ed , no shear reinforcement is required. Shear is ok

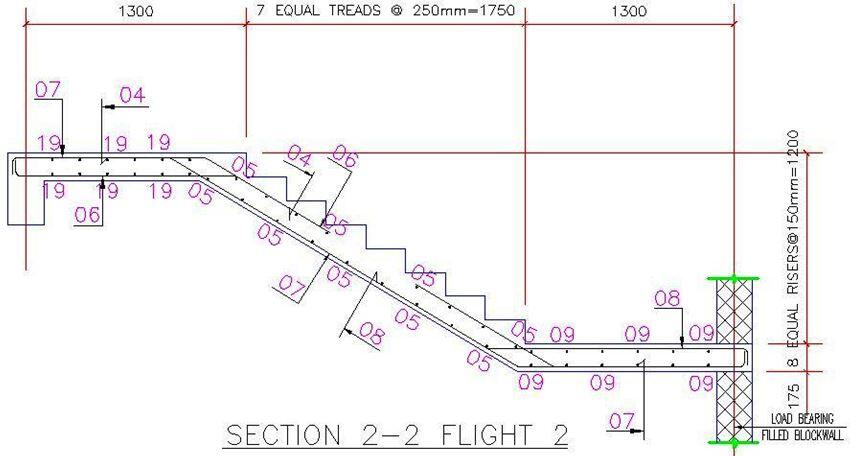
Staircase reinforcement details

To download the full paper in PDF format, click HERE