Tensile membrane structures, characterized by their lightweight and expressive forms, have captivated architects and engineers for decades. However, achieving their desired shape while ensuring structural integrity poses a unique challenge. This is where form finding, an important optimization process, becomes indispensable.
Tensile membrane structures are defined by their doubly curved surfaces and rely on inherent tension for stability. This curvature plays a critical role in distributing prestresses across the membrane, leading to its structural integrity. Without appropriate curvature, desired force distribution cannot occur, rendering the surface structurally unsound. This intrinsic quality of opposing curvatures is fundamental to membrane structures.
However, traditional architectural drawing methods fall short of capturing these complex surfaces. Instead, specialized approaches are required to model and analyze the force flow within the membrane. This process, referred to as form finding, aims to identify the optimal shape that achieves equilibrium under given boundary conditions.
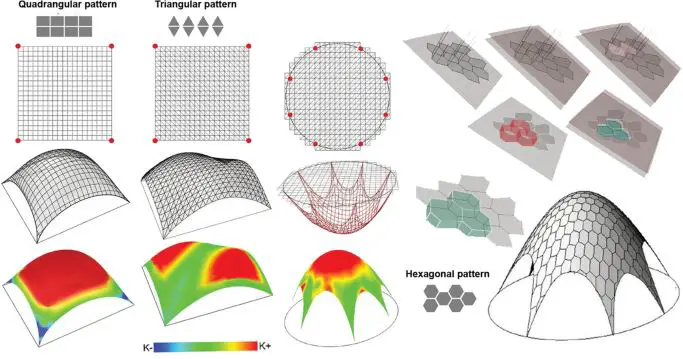
Unlike conventional structures governed by bending rigidity, tensile membranes resist loads through in-plane tension. This inherent flexibility allows for diverse geometries but necessitates a form-finding process to determine a shape that satisfies both equilibrium (balance of internal forces and external loads) and architectural intent.
In essence, form finding seeks to establish an equilibrium surface within defined constraints. By iteratively adjusting boundary conditions and analyzing stress distribution, it strives to produce a surface that is not only aesthetically pleasing and functionally appropriate but also structurally viable. The boundary conditions encompass the edge elements and support points that define the membrane’s physical limitations. Finally, the achieved equilibrium form ensures that all points on the surface remain in a state of physical balance under the applied tensile load.
The application of tensile load to a membrane surface can expose areas of compression, manifesting as wrinkles. This wrinkle formation indicates an uneven distribution of prestress, hindering the ability of the surface to achieve equilibrium.
Form Finding Process
Form-finding methodology encompasses two primary approaches: physical and numerical.
Physical Modelling
The initial forays into tensile membrane structures relied heavily on physical models. Soap films and flexible fabric pieces were employed to create physical models that guided subsequent fabrication. Soap films, due to their exceptional thinness and lack of shear resistance, proved particularly adept at visualizing force distribution and arriving at optimal forms.
This practice of physical modelling in architecture remains relevant today. It offers an economical and rapid means to explore design solutions prior to delving into numerical analysis, often leading to more creatively inspired forms. Additionally, physical models can enhance comprehension of complex surfaces through three-dimensional visualization.
Numerical Modelling
Technological advancements in numerical modelling and computer capabilities have profoundly impacted the design, manufacturing, and analysis of membrane systems. In numerical form finding, the membrane surface is discretized into a mesh, upon which both manufacturing and structural analysis are conducted.
This approach offers independence from the membrane’s physical properties, such as thickness or elasticity. Various numerical methods, including Force Density, Dynamic Relaxation, and Finite Element Methods, are employed to achieve the equilibrium surface.
The design and analysis of membrane building systems witnessed a significant turning point with the Munich Olympic Stadium project in 1972. Klaus Linkwitz’s pioneering introduction of the Force Density Method in 1971 marked the first numerical approach specifically tailored to the unique needs of tensile structures.

During form finding, membrane surfaces can be conceptualized as fluid systems. Their final shape emerges from the interplay between defined boundary conditions and the applied tensile load distribution. Our control over the membrane’s geometry lies solely in manipulating these boundary conditions and the load distribution ratios. By iteratively adjusting these variables, the resulting form is refined based on various criteria, including structural capacity, functionality, and aesthetic integration.
However, it’s important to note that modifications to the form directly impact the membrane’s structural capacity. Therefore, ensuring the structural adequacy of the membrane against anticipated loads takes precedence over aesthetic considerations and functionality. This prioritization is particularly critical for snow loads, given the inherent limitations in the mechanical properties of membrane materials.
Form Finding Methods
Several form finding methods exist, each offering distinct advantages and complexities. Here, we delve into three prominent approaches:
1. Physical Soap Film Modelling: This classical technique utilizes soap films stretched across a physical boundary representing the desired supports. The minimal surface formed by the soap film, driven by surface tension, embodies the equilibrium state and serves as a direct physical analogue of the optimal shape. While elegant and intuitive, limitations arise from scalability and complex boundary conditions.
2. Force Relaxation Methods: These computational approaches, such as dynamic relaxation, mimic the relaxation process of a physical system towards equilibrium. An initial geometry is iteratively adjusted based on unbalanced forces, gradually converging towards a stable form. The method’s versatility allows for incorporating various boundary conditions and material properties, but convergence speed and numerical stability require careful consideration.
3. Energy Minimization Techniques: Based on variational calculus, these methods seek the minimum potential energy configuration of the system. By formulating the energy function encompassing membrane strain, boundary constraints, and external loads, the optimal shape can be obtained through numerical minimization algorithms. This approach offers a robust framework for complex geometries and material behaviours, but computational demands can be significant.
The choice of form-finding method depends on various factors, including project scale, complexity, desired accuracy, and available computational resources. In practice, hybrid approaches combining physical and numerical methods are often employed, leveraging the strengths of each technique.
Benefits of Form Finding
Beyond achieving equilibrium, form finding plays a crucial role in:
- Optimizing material usage: By distributing tension efficiently, form finding minimizes required membrane material, leading to cost-effective and sustainable designs.
- Controlling deflections: Targeted form finding can mitigate excessive deflections under wind and snow loads, enhancing structural performance and serviceability.
- Integrating architectural vision: The iterative nature of form finding allows for incorporating aesthetic considerations and tailoring the shape to harmonize with the architectural intent.
Conclusion
In conclusion, form finding lies at the heart of successful tensile membrane structures. By creating the required force equilibrium in the structure, it enables the creation of lightweight, efficient, and visually striking structures that push the boundaries of architectural expression. As computational tools and design methodologies continue to evolve, form finding will remain a vital tool for shaping the future of tensile membrane architecture.










