Betti’s Theorem of Reciprocal Work

Betti’s Theorem, also known as the Maxwell-Betti Reciprocal Work Theorem, is a fundamental principle in structural analysis. Betti’s theorem of reciprocal works states that in any elastic system, the work performed by a load of state 1 along displacement caused by a load of state 2 equals the work performed by a load of state 2 along displacement caused by a load of state 1.

In other words, it states that for a linear elastic structure subjected to two sets of forces, the work done by the first set of forces in acting through the displacements produced by the second set of loads is equal to the work done by the second set of loads in acting through the displacements produced by the first set.

Reciprocal theorems reflect the fundamental properties of any linear statistically determinate or indeterminate elastic systems. These theorems find extensive application in the analysis of redundant structures.

Proof of Betti’s theorem

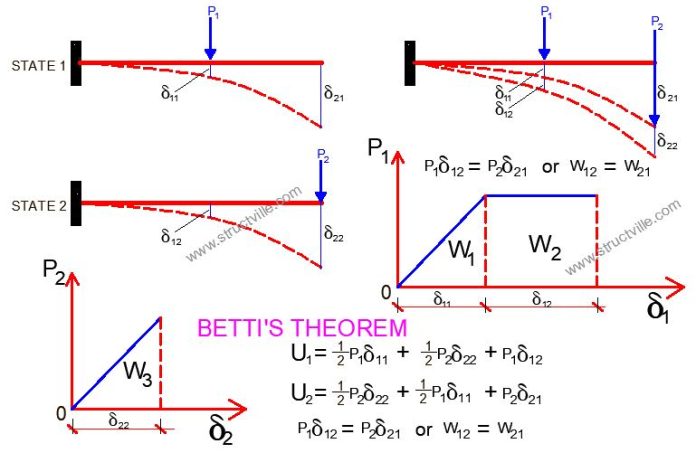
Let us consider an elastic structure subjected to loads P₁ and P₂ separately; let us call it the first and second states (Figure 1). Set of displacements Δ_mn for each state are shown below. The first index m indicates the direction of the displacement and the second index n denotes the load, which causes this displacement.

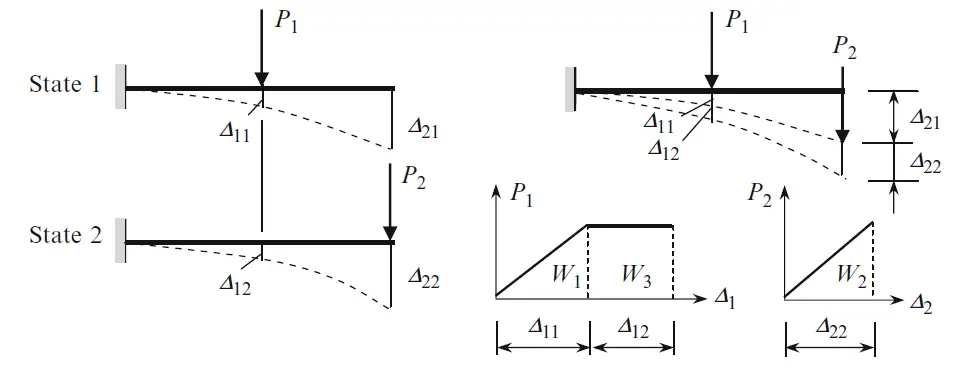
Thus, Δ₁₁ and Δ₁₂ are displacements in the direction of load P₁ due to load P₁ and P₂, respectively, Δ₂₁ and Δ₂₂ are displacements in the direction of load P₂ due to load P₁ and P₂, respectively.

Let us calculate the strain energy of the system by considering consequent applications of loads P₁ and P₂, i.e., state 1 is additionally subjected to load P₂. The total work done by both of these loads consists of three parts:

1. Work done by the force P₁ on the displacement Δ₁₁. Since load P₁ is applied statically (from zero to P₁ according to triangle law), then W₁ = P₁Δ₁₁/2.
2. Work done by the force P₂ on the displacement Δ₂₂. Since load P₂ is applied statically, then W₂ = P₂Δ₂₂/2.
3. Work done by the force P₁ on the displacement Δ₁₂; this displacement is caused by load P₂. The load P₁ approached its maximum value P₁ before the application of P₂. The corresponding P₁–Δ₁ diagram is shown in Figure 1, so W₃ = P₁Δ₁₂.

Since potential energy U equals to the total work, then;

U = ½P₁Δ₁₁ + ½P₂Δ₂₂ + P₁Δ₁₂

On the other hand, considering of application of load P₂ first and then P₁, i.e., if state 2 is additionally subjected to load P₁, then potential energy U equals;

U = ½P₂Δ₂₂ + ½P₁Δ₁₁ + P₂Δ₂₁

Since strain energy does not depend on the order of loading, then the following fundamental relationship is obtained;
P₁Δ₁₂ = P₂Δ₂₁ or W₁₂ = W₂₁

Work W₁₂ can be positive or negative. It is only zero if and only if the displacement of the point of application of force P₁ produced by force P₂ is zero or perpendicular to the direction of P₁.

A Simple Analogy

Imagine two people pushing against each other. Person A pushes person B with a certain force, resulting in a displacement of person B. Simultaneously, person B pushes person A with an equal and opposite force, causing a displacement of person A. Betti’s Theorem states that the work done by person A on person B is equal to the work done by person B on person A.

Implications and Applications

At its core, Betti’s Theorem establishes a reciprocal relationship between loads and displacements in a linear elastic system. This principle has far-reaching implications in structural engineering:  

• Influence Lines: It is instrumental in constructing influence lines, which are essential for analyzing indeterminate structures under moving loads.  
• Boundary Element Method: This numerical method, widely used in engineering, is based on Betti’s Theorem.  
• Analysis of statically indeterminate structures using force method: It simplifies the calculation of influence coefficients when using the force method to analyse statically indeterminate structures.
• Structural Optimization: It contributes to the design of compliant mechanisms through topology optimization techniques.  

Limitations

It is important to remember that Betti’s Theorem is applicable only to linear elastic structures. This means that the material of the structure must obey Hooke’s law, and the deformations must be small. In conclusion, Betti’s Theorem is a powerful tool for engineers and scientists, providing a foundation for understanding and analyzing the behaviour of structures under various loading conditions.