ChatGPT and Civil Engineering Calculations

Within the last few months, ChatGPT has caused a disruption in the way information is accessed on the internet. It appears that artificial intelligence is becoming capable of doing virtually everything, and the civil engineering/construction industry is not left out.

ChatGPT is an AI-based language model designed to engage in natural language conversations with users. It is part of the GPT (Generative Pre-trained Transformer) family of models developed by OpenAI. GPT models are trained on a vast amount of text data from the internet, allowing them to generate human-like responses to a wide range of prompts.

ChatGPT utilizes deep learning techniques, particularly Transformer architectures, to understand and generate text based on the context provided. It can process and generate coherent and contextually relevant responses by analyzing the patterns and structures of the input text.

In this article, we are going to review the response of ChatGPT to various calculations and examples relating to civil engineering.

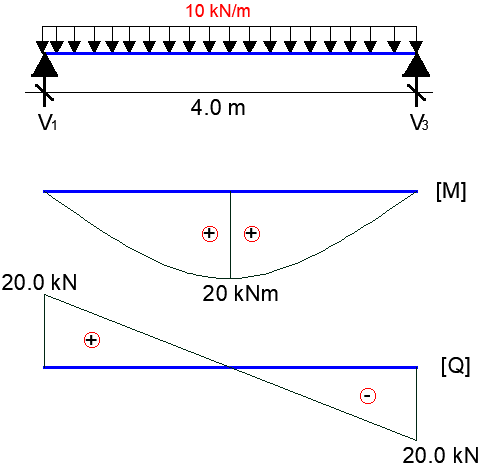
QUESTION 1: A 4m span beam is simply supported at both ends and subjected to a uniformly distributed load of 10 kN/m at the midspan. What are the support reactions and the maximum bending moment?

CHATGPT:
To determine the support reactions and the maximum bending moment for the given beam, we can apply the principles of statics and beam analysis.

First, let’s consider the support reactions:

1. Vertical Reaction at Each Support: Since the beam is simply supported at both ends, each support will provide an equal and opposite vertical reaction. Let’s denote the upward reaction at each support as Rv.

The total load on the beam is the uniformly distributed load of 10 kN/m over the entire span. As the load is symmetrical, the load acting at the midspan is half of the total load, i.e., (10 kN/m) * (4 m) / 2 = 20 kN.

According to the principle of equilibrium, the sum of the vertical forces must be zero:
2Rv = 20 kN
Rv = 10 kN

Therefore, each support reaction is 10 kN vertically upward.

Next, let’s calculate the maximum bending moment:

The maximum bending moment occurs at the midspan of the beam when it is subjected to a uniformly distributed load. In this case, the maximum bending moment can be determined using the formula:

Mmax = (wL^2) / 8

Where:
Mmax is the maximum bending moment,
w is the uniformly distributed load (10 kN/m),
L is the span length (4 m).

Substituting the values into the formula, we get:

Mmax = (10 kN/m) * (4 m)^2 / 8
Mmax = 20 kNm

Therefore, the maximum bending moment in the beam is 20 kNm.

To summarize:

• The support reactions at each end are 10 kN vertically upward.
• The maximum bending moment in the beam is 20 kNm.

VERDICT: CHATGPT is correct with the bending moment, but wrong with the support reaction. The total load acting on the beam is not half of the total load, but simply the total area of the load (10 x 4 = 40 kN). So the total load on the beam is 40 kN, making the support reactions 20 kN at each support.

QUESTION 2: For the beam described above, what is the deflection at 1.5m from the left-hand side support?

CHATGPT Response:
To calculate the deflection at a specific point along the beam, such as 1.5m from the left-hand side support, we can use the formula for deflection of a simply supported beam under a uniformly distributed load.

The formula for the deflection at a distance x from the left support of a simply supported beam with a uniformly distributed load can be given as:

δ = (5 * w * x^4) / (384 * E * I)

Where:
δ is the deflection at the given point (1.5m in this case),
w is the uniformly distributed load (10 kN/m),
x is the distance from the left support to the point where the deflection is calculated (1.5m),
E is the modulus of elasticity of the material the beam is made of,
I is the moment of inertia of the beam’s cross-section.

The modulus of elasticity (E) and moment of inertia (I) depend on the properties and dimensions of the beam. Without that information, it is not possible to calculate the deflection accurately. The specific values for E and I would need to be known or provided to determine the deflection at a specific point on the beam.

Please note that calculating beam deflection involves additional assumptions, such as the beam being linearly elastic and having a constant cross-section throughout its length. Different beam materials and configurations may require different deflection formulas and considerations.

VERDICT: CHATGPT’s response is wrong. The AI model used a general equation for calculating the deflection at the mid-span of a simply supported beam subjected to a uniformly distributed load to calculate the deflection at a point that is not the mid-span. You cannot merely substitute any value of x into the famous deflection equation [δ = (5wx⁴) / (384EI)] if x is not the midspan.

The general equation for calculating the deflection at any point on a simply supported beam subjected to a uniformly distributed load is;

EIδ = -wLx³/12 + wx⁴/24 + (wL³/24)x

at x = L/2 (mid-span)
δ = [-wL(L/2)³/96 + w(L/2)⁴/24 + (wL³/24)L/2]/EI
δ = [-wL⁴/96+ wL⁴/384 + wL⁴/48]/EI = 5wL⁴/384EI

At x = 3L/8 (1.5m from the left-hand side), the value of the deflection can also be calculated.

QUESTION 3: Your approach to the above question is wrong. The formula is only valid for the mid-span of the beam and not anywhere else.

CHATGPT:
I apologize for the confusion caused by my previous response. You are correct, the formula I mentioned is applicable only for the deflection at the mid-span of the beam under a uniformly distributed load.

To determine the deflection at a specific point other than the mid-span, we need to use a different approach. In this case, we can calculate the deflection using the double integration method.

The deflection at a distance x from the left support can be calculated using the following steps:

1. Calculate the reaction forces at the supports using the total load and beam span as explained in the previous response. In this case, each support reaction is 10 kN vertically upward.
2. Determine the equations for the elastic curve in each segment of the beam. The beam can be divided into two segments: one from the left support to the point of interest (1.5m), and the other from the point of interest to the right support.
3. Integrate the equations of the elastic curve twice to obtain the deflection equation for each segment.
4. Apply the appropriate boundary conditions to determine the constants of integration.
5. Evaluate the deflection equation at the point of interest (1.5m) to obtain the deflection at that location.

Without specific information about the beam’s material, cross-section, and other relevant details, it is not possible to provide an accurate calculation of the deflection at 1.5m from the left support. To determine the deflection accurately, you would need to know the properties of the beam and use the appropriate equations and calculations based on those properties.

VERDICT: CHATGPT’s response is correct.

QUESTION 4: A rectangular reinforced concrete beam with a depth of 500mm and a width of 250mm is subjected to an ultimate bending moment of 95 kNm. What is the area of steel required if the yield strength of steel is 500 MPa, the characteristic compressive strength of concrete is 30 MPa, and the concrete cover is 35 mm.

CHATGPT:
To determine the area of steel required in a reinforced concrete beam, we need to consider the equilibrium of forces and the stress limits of both the concrete and steel.

1. Calculate the section modulus: The section modulus (Z) of a rectangular beam can be calculated using the formula: Z = (b * d^2) / 6 Where: b is the width of the beam (250 mm), d is the effective depth of the beam (depth – cover – steel diameter).

Given:
Depth of the beam (d) = 500 mm
Concrete cover (c) = 35 mm
Assuming the diameter of the steel reinforcement as 8 mm (commonly used size),
Effective depth (d) = Depth – Cover – Steel diameter = 500 mm – 35 mm – 8 mm = 457 mm

Now, calculate the section modulus:
Z = (250 mm * (457 mm)^2) / 6
Z = 20,610,417 mm^3

2. Calculate the stress in the concrete: The stress in the concrete (σ_c) can be calculated using the formula:
   σ_c = M / Z
   Where: M is the ultimate bending moment (95 kNm).

Given: Ultimate bending moment (M) = 95 kNm

Convert the moment to Nmm: M = 95 kNm * 10^6 Nm/kNm M = 95,000,000 Nmm

Now, calculate the stress in the concrete:
σ_c = 95,000,000 Nmm / 20,610,417 mm^3
σ_c = 4.61 MPa

3. Calculate the required area of steel: The required area of steel (A_s) can be determined using the formula:
   A_s = (σc * Z) / σs
   Where: σ_s is the yield strength of the steel reinforcement (500 MPa).

Given: Yield strength of steel (σ_s) = 500 MPa

Now, calculate the required area of steel:
A_s = (4.61 MPa * 20,610,417 mm^3) / (500 MPa)
A_s = 189.23 mm^2

Therefore, the required area of steel in the reinforced concrete beam is approximately 189.23 mm^2.

Verdict: Uhmmmmm ???

QUESTION 5: Can you carry out the calculation again according to the requirements of the Eurocode?

CHATGPT: Certainly! I apologize for the oversight. Here’s the calculation based on the requirements of the Eurocode for reinforced concrete design.

1. Calculate the design bending moment (M_d): The design bending moment (M_d) is calculated by dividing the ultimate bending moment by a factor of safety, typically taken as 1.5 for ultimate limit state design.
   M_d = 95 kNm / 1.5 M_d = 63.33 kNm
2. Calculate the effective depth (d): The effective depth (d) is calculated as the overall depth minus the concrete cover and half the diameter of the reinforcement.
   d = Depth – Cover – (Steel diameter / 2)
   d = 500 mm – 35 mm – (8 mm / 2)
   d = 457 mm
3. Determine the design compressive strength of concrete (f_cd): The design compressive strength of concrete (f_cd) is calculated by dividing the characteristic compressive strength of concrete (f_ck) by a factor of safety, typically taken as 1.5 for normal strength concrete.
   f_ck = 30 MPa / 1.5 f_ck = 20 MPa
4. Calculate the design tensile strength of steel (f_td): The design tensile strength of steel (f_td) is calculated by dividing the characteristic yield strength of the reinforcement (f_yk) by a factor of safety, typically taken as 1.15.
   f_yk = 500 MPa / 1.15 f_yk = 434.78 MPa
5. Determine the design moment capacity (M_rd): The design moment capacity (M_rd) is calculated using the following formula:
   M_rd = (f_td * A_s * (d – a_s / 2)) / γ_M
   
   Where:
   A_s is the area of steel,
   a_s is the distance from the centroid of the steel to the extreme compression fiber,
   γ_M is the partial factor for moment resistance (taken as 1.0 for the ultimate limit state design).

Since the beam is under-reinforced according to Eurocode, the limiting value of a_s is the smaller of:
a_s = β_1 * (d – a_s / 2) or a_s = β2 * (d – xu)

For rectangular beams, β_1 = 0.5 and β_2 = 0.8.

Assuming a_s = 35 mm (same as the concrete cover), we can calculate the value of x_u (the depth of the neutral axis):
x_u = β_2 * d x_u = 0.8 * 457 mm
x_u = 365.6 mm

Now we can substitute the values into the formula:
M_rd = (f_td * A_s * (d – a_s / 2)) / γ_M
63.33 kNm = (434.78 MPa * A_s * (457 mm – 35 mm / 2)) / 1.0

Solving for A_s:
A_s = (63.33 kNm * 1.0) / (434.78 MPa * (457 mm – 35 mm / 2))
A_s ≈ 50.57 mm^2

Therefore, according to the Eurocode requirements, the required area of steel in the reinforced concrete beam is approximately 50.57 mm^2.

VERDICT: WRONG

QUESTION 6: Your solution is a bit strange. The bending moment provided was stated as an ultimate moment. Furthermore, even if the bending moment is ‘unfactored’, are you supposed to multiply or divide action effects with the partial factor of safety?

CHATGPT: I apologize for the confusion in my previous response. You are correct, for ultimate limit state design according to Eurocode, the ‘unfactored’ ultimate bending moment should be used directly in the calculations. Additionally, the action effects should be multiplied by the appropriate partial factor of safety.

Let’s recalculate the required area of steel according to the Eurocode requirements:

1. Calculate the effective depth (d) as before:
   d = Depth – Cover – (Steel diameter / 2)
   d = 500 mm – 35 mm – (8 mm / 2) d = 457 mm
2. Determine the design compressive strength of concrete (f_cd): The design compressive strength of concrete (f_cd) is calculated by dividing the characteristic compressive strength of concrete (f_ck) by the appropriate partial factor of safety for concrete. For normal-strength concrete, this factor is taken as 1.5.
   f_cd = 30 MPa / 1.5
   f_cd = 20 MPa
3. Calculate the design tensile strength of steel (f_td): The design tensile strength of steel (f_td) is calculated by dividing the characteristic yield strength of the reinforcement (f_yk) by the appropriate partial factor of safety for steel. For reinforcing steel, this factor is typically taken as 1.15.
   f_td = 500 MPa / 1.15
   f_td = 434.78 MPa
4. Determine the required area of steel (A_s): The required area of steel (A_s) can be calculated using the formula:
   A_s = (M_d * 10^6) / (f_td * (d – a_s / 2))
   
   Where: M_d is the ‘unfactored’ ultimate bending moment (95 kNm),
   f_td is the design tensile strength of steel (434.78 MPa),
   d is the effective depth of the beam (457 mm),
   a_s is the distance from the centroid of the reinforcement to the extreme compression fiber.

Assuming a_s = 35 mm (same as the concrete cover), we can substitute the values into the formula:
A_s = (95 kNm * 10^6) / (434.78 MPa * (457 mm – 35 mm / 2))
A_s ≈ 515.88 mm^2

Therefore, according to the Eurocode requirements, the required area of steel in the reinforced concrete beam is approximately 515.88 mm^2.

VERDICT: This particular solution is very close to being acceptable, even though the approach used in the calculation of the lever arm is a bit crude (considering the EC2 stress block). We know that for singly reinforced sections, the approach used by ChatGPT shouldn’t make any much difference in the design results (using the effective depth of 457mm, the area of steel required is 503 mm²).

Furthermore, ChatGPT made its own assumptions (such as selecting its own diameter of reinforcement), but it didn’t consider the diameter of links in calculating the effective depth. It was also able to pick the material partial factors of safety correctly. However, it erroneously used the term ‘unfactored moment’ which it picked from the question I posed to it. It probably assumed ‘unfactored moment’ to mean ‘design moment’.

QUESTION 7: A 500 mm diameter concrete pile is driven 12m deep into a homogenous pure clay soil with an effective cohesion of 18 kPa. What is the load-carrying capacity of the pile as a result of shaft friction?

CHATGPT:

To determine the load-carrying capacity of the pile due to shaft friction, we can use the principles of soil mechanics and the formula for calculating the ultimate shaft resistance in cohesive soils. The ultimate shaft resistance can be calculated using the following equation:

Qs = π * D * L * c’

Where:
Qs is the ultimate shaft resistance,
D is the diameter of the pile,
L is the depth of penetration,
c’ is the effective cohesion of the soil.

Given: Diameter of the pile (D) = 500 mm Depth of penetration (L) = 12 m Effective cohesion of the soil (c’) = 18 kPa

Converting the diameter to meters: D = 500 mm / 1000 D = 0.5 m
Converting the effective cohesion to kN/m²: c’ = 18 kPa * 1 kN/m² / 1000 Pa
c’ = 0.018 kN/m²

Substituting the values into the formula: Qs = π * 0.5 m * 12 m * 0.018 kN/m²
Qs ≈ 3.83 kN

Therefore, the load carrying capacity of the pile due to shaft friction is approximately 3.83 kN.

VERDICT: WRONG

QUESTION 8: But kPa is the same thing as kN/m^2

ChatGPT: You’re absolutely right, I apologize for the confusion in my response. kPa (kilopascal) is indeed equivalent to kN/m² (kilonewton per square meter), representing the unit of pressure or stress.

Given that the effective cohesion (c’) is already in kPa, we can directly substitute the values into the formula:

Qs = π * D * L * c’
Qs = π * 0.5 m * 12 m * 18 kPa
Qs ≈ 34.56 kN

Therefore, the load-carrying capacity of the pile due to shaft friction is approximately 34.56 kN.

VERDICT: This particular solution is correct. But out of curiosity, it is important to find out if the AI model picked the right equation.

QUESTION 9: Did you consider the adhesion factor (α) in your calculation?

I apologize for not considering the adhesion factor (α) in the calculation. The adhesion factor takes into account the reduction in the effective cohesion along the pile shaft due to factors such as pile installation method and soil characteristics.

The equation to calculate the ultimate shaft resistance considering the adhesion factor is:

Qs = α * π * D * L * c’

The adhesion factor (α) typically ranges between 0.5 and 1.0, depending on the soil conditions and installation method. Without specific information regarding the adhesion factor for your case, it is challenging to provide an accurate value. However, for a conservative estimate, let’s assume α = 0.5.

Using this assumption, we can calculate the load-carrying capacity of the pile due to shaft friction:

Qs = 0.5 * π * 0.5 m * 12 m * 18 kPa
Qs ≈ 8.14 kN

Therefore, considering an adhesion factor (α) of 0.5, the load carrying capacity of the pile due to shaft friction is approximately 8.14 kN.

VERDICT: For driven piles in clay soils with effective cohesion less than 40 kPa, the recommended value of the adhesion factor is 1.0. I guess we can forgive ChatGPT.

Conclusion

In conclusion, ChatGPT can be a useful tool for carrying out civil engineering calculations. However, it can only get better. As can be seen from this article, it can quickly perform calculations, especially for problems involving popular equations and well-known theories. For other advanced calculations, extreme caution should be used.

It is important to note that ChatGPT is an AI language model and does not have access to specific project details or real-time data. Therefore, its responses are based solely on the information provided and the knowledge it has been trained on.

While ChatGPT can provide valuable assistance in performing calculations, it is essential to exercise caution and independently verify the results as can be seen in this article. It appears that it is heavily influenced by the input data, and the expertise of the engineer is required to drive it in the right direction.

Engineering calculations often require careful consideration of various factors, including applicable codes, standards, material properties, and site-specific conditions. Therefore, it is always recommended to consult with qualified engineers and professionals to ensure accurate and reliable results.