Critical Depth for Skin Friction in Piles

Skin friction is the resistance developed along the sides of the pile shaft due to the interaction between the pile and the surrounding soil. It is one of the primary mechanisms by which piles transfer load to the soil. The magnitude of skin friction is influenced by various factors, including soil type, pile geometry, installation method, and load conditions.

In geotechnical engineering, the vertical effective stress, denoted by σ’, normally increases with depth. As a result, it should be logical that the magnitude of skin friction in piles should increase infinitely with increasing depth. In reality, the magnitude of skin friction will not continue to increase infinitely with increasing depth. It was formerly thought that at a certain depth, the value of skin friction in piles would become constant. This particular depth is called the ‘critical depth’.

The critical depth for skin friction is the depth below the ground surface at which the increase in pile diameter does not contribute significantly to the overall capacity of the pile. In other words, beyond this critical depth, the additional skin friction developed due to an increase in pile diameter becomes negligible. Determining the critical depth is crucial because it helps optimize the design and construction of piles, considering both cost-effectiveness and structural efficiency.

As shown in Figure 1, skin friction was assumed to increase up to the critical depth and then maintain a constant value.

d_c = critical depth
S_c = skin friction at the critical depth (K.σ’_c .tanδ)
σ’_c = effective stress at critical depth

The following approximations were assumed for the critical depth

• Critical depth for loose sand = 10d (d is the pile diameter or the width)
• Critical depth for medium-dense sand = 15d
• Critical depth for dense sand = 20d

However, this theory does not explain recent observations made from precise pile load test data. According to recent experiments, skin friction will not become absolutely constant as was once believed.

Experimental Evidence of Critical Depth

A typical variation in skin friction that occurs with increasing pile depth is shown in Figure 2. As can be seen in Figure 2, the assumption proposing constant skin friction below the critical depth is not supported by the results obtained from the experiments.

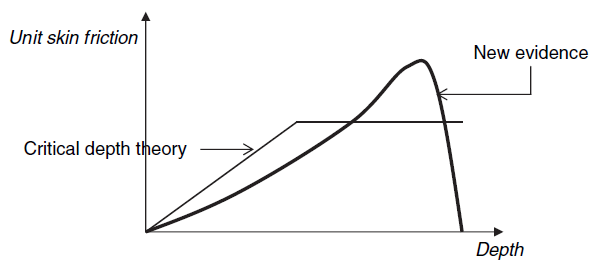
The skin friction has a tendency to increase with depth, and it reaches its maximum value right above the tip of the pile. After then, there would be a significant reduction in skin friction. At the moment, there is no theory that can adequately explain the observations made in the field. The critical depth theory is still widely used in engineering today because there is no more advanced alternative.

Reasons for limiting skin friction in Piles

In order to explain why the skin friction does not increase infinitely with depth as the skin friction equation suggested, the following explanations have been presented.

Unit Skin Friction = K∙σ’∙tanδ
σ’ = γd

1. The value of K presented above is determined by the soil angle of friction, denoted by φ’. As one goes deeper, the angle of internal friction angle typically reduces. As a result, the K value reduces as depth increases (Kulhawy 1983).
2. The aforementioned equation for skin friction does not hold true at high-stress levels because the sand particles have to adjust their orientation.
3. A reduction in the magnitude of friction is experienced by the shaft as the pile depth increases. (See Figure 3) (Randolph et al. 1994).

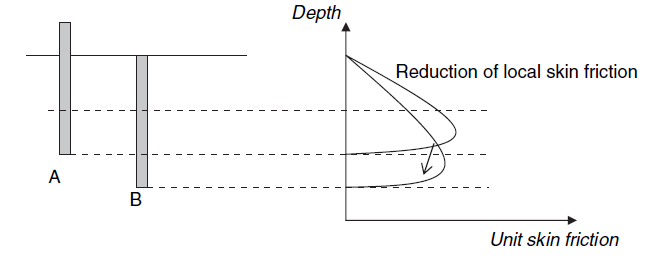
Let’s assume a pile was driven to a depth of 3m (10 ft), and the unit skin friction was measured at a depth of 1.5m (5 ft). If we also assume that the pile was driven further to a depth of 4.5m (15 ft) and that the unit skin friction was measured at the same depth of 1.5m( 5 ft). It has been reported that the second scenario has a lower unit skin friction at a distance of 1.5m.

Figure 3 demonstrates that as the pile is driven further into the earth, the local skin friction experiences a reduction. According to NAVFAC DM 7.2, the maximum value of skin friction and end bearing capacity is attained after 20 diameters within the bearing zone. This is the case regardless of the bearing material.

Solved Example on Critical Depth

(Calculation after Rajapakse, 2008)

Find the skin friction and end-bearing capacity of the pile shown. Assume that critical depth is achieved at 20 ft into the bearing layer. The pile diameter is 1 ft, and other soil parameters are as shown in the figure.

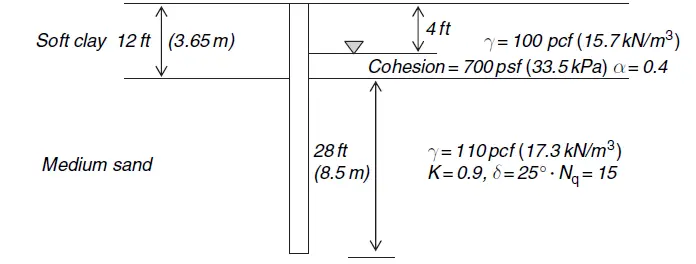
Solution
The skin friction is calculated in the overburden soil. In this case, skin friction is calculated in the soft clay. Then the skin friction is calculated in the bearing layer (medium sand) assuming the skin friction attains a limiting value after 20 diameters (critical depth).

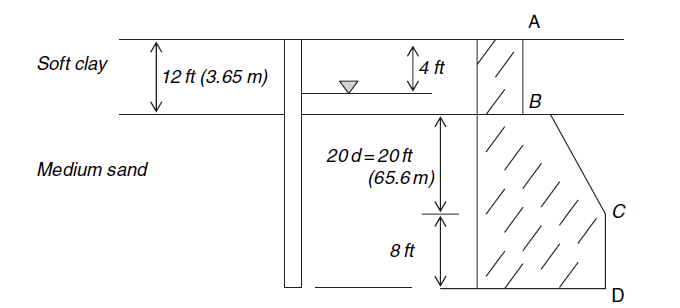
STEP 1: Find the skin friction from A to B.
Skin friction in soft clay = α × c × perimeter surface area
= 0.4 × 700 × πdL = 0.4 × 700 × π × 1 × 12 = 10,560 lbs = 46.9 kN

STEP 2: Find the skin friction from B to C.
Skin friction in sandy soils S = K∙σ’∙tanδ × A_p

S = skin friction of the pile
σ’ = average effective stress along the pile shaft
Average effective stress along pile shaft from B to C = (σ_B + σ_C)/2
σ_B = effective stress at B
σ_C = effective stress at C

To obtain the average effective stress from B to C, find the effective stresses at B and C and obtain the average of those two values.
σ_B = 100 × 4 (100 – 62.4) × 8 = 700.8 lb/ft² (33.6 kPa)
σ_C = 100 × 4 (100 – 62.4) × 8 + (110 – 62.4) × 20 = 1452.8 lb/ft² (69.5 kPa)
Average effective stress along pile shaft from B to C = (700.8 + 1452.8)/2 = 1076.8 lb/ft²

Skin friction from B to C = K∙σ’∙tanδ × A_p = 0.9 × 1076.8 × tan 25 × (π × 1 × 20) = 28,407 lbs

STEP 3: Find the skin friction from C to D.
Skin friction reaches a constant value at point C, 20 diameters into the bearing layer.
Skin friction at point C = K∙σ’_v∙tanδ × A_p

σ’_v at point C = 100 × 4 (100 – 62.4) × 8 (110 – 62.4) × 20 = 1,452.8 lb/ft²
Unit skin friction at point C = 0.9 × 1,452.8 × tan 25 = 609.7 lb/ft² (29 kPa)
Unit skin friction is constant from C to D. This is because skin friction does not increase after the critical depth.
Skin friction from C to D = 609.7 × surface perimeter area = 609.7 × (π × 1 × 8) = 15,323.4 lbs (68.2 kN)

Summary
Skin friction in soft clay (A to B) = 10,560 lbs
Skin friction in sand (B to C) = 28,407 lbs
Skin friction in sand (C to D) = 15,323 lbs
Total = 54,290 lbs (241 kN)

STEP 4: Compute the end bearing capacity.
End bearing capacity also reaches a constant value below the critical depth.
End bearing capacity = q × N_q × A

q = effective stress at pile tip
N_q = bearing capacity factor (given to be 15)
A = cross-sectional area of the pile

If the pile tip is below the critical depth, q should be taken at critical depth. In this example, the pile tip is below the critical depth, which is 20 diameters into the bearing layer. Hence, q is equal to the effective stress at the critical depth (point C).

Effective stress σ’_v at point C = 100 × 4 (100 – 62.4) × 8 (110 – 62.4) × 20 = 1,452.8 lb/ft²
End bearing capacity = qN_qA = 1,452.8 × 15 × (πd²/4) = 17,115 lbs

Total ultimate capacity of the pile = total skin friction + end bearing = 54,290 + 17,115 = 71,405 lbs (317.6 kN)

Conclusion

The critical depth for skin friction in piles is a crucial parameter for the design of piles in sand. It is believed to depend on factors such as soil type, pile diameter, and installation techniques. The determination of the critical depth is very important to ensure that the shaft friction of the pile is not overestimated, thereby ensuring the stability and safety of structures supported by piles. Ongoing research and advancements in geotechnical engineering continue to enhance our understanding of the critical depth and its significance in pile foundation design.

Reference

Rajapakse R. (2008): Pile Design for Structural and Geotechnical Engineers. ISBN: 978-0-08-055916-2 Butterworth-Heinemann