Calculation of Collapse Settlement of Collapsible Soils

Civil engineers are always faced with one challenge or another on-site, and one of the major challenges on-site has to do with the nature of the soil to support the structure to be constructed. Some soils exhibit excessive change in volume under constant load and changes in moisture content. Under field conditions, if the addition of water under constant load causes the void ratio to reduce drastically, the soil is said to have collapsed.

These soils are predominantly found in the arid regions and appear strong and stiff in their dry natural state, but lose strength and undergo high compression upon wetting.  According to Behzad (2013), almost all natural deposits of collapsible soils are either debris flow deposits or wind deposited soils (loess).

Soils which exhibit this behaviour are usually unsaturated granular soils which in a loose state are maintained by apparent cohesion. This apparent cohesion may be due to the presence of clays at the intergranular contact areas or the accumulation of soluble salts as binders (Murthy, 2012). In South-Western Nigeria, collapsible soils have been observed and studied by Owolabi and Ola (2014).

Collapsible Soils

For a soil sample to collapse, the soil structure must have an open, partially unstable, and unsaturated fabric which must be held in place by apparent cohesion. On wetting and application of high enough stress, the soil fabric will be expected to collapse.

For compacted cohesive soils, the collapse behaviour will depend on the percentage of fines, the moulding water content, the dry density, and the compaction energy employed Murthy (2012). Any soil compacted at the dry side of the optimum moisture content and at low dry density will also be expected to develop a collapsible structure.

Calculation of Collapse Settlement

A method of calculating the collapse settlement of a soil sample was suggested by Jennings and Knight (1975) and reported by Murthy (2012). This involves carrying out double oedometer tests of identical undisturbed samples in the laboratory. Both specimens are kept under a constant pressure of 1 kPa for a period of 24 hours at their natural moisture content after which one specimen is flooded and the other allowed to remain in its natural state.

After flooding for 24 hours, the consolidation test is allowed to progress as usual after which the e-LogP curve is plotted for both samples. The collapse settlement is calculated in two parts according to equations (1) and (2).

S₁ = Δe_nH /(1 + e₀)  ————————- (1)
S₂ = Δe_cH /(1 + e₀)  ————————- (2)

Where;
Δe_n =  Change in void ratio due to load ΔP as per the e-logP plot without change in moisture content
Δe_c =  Change in void ratio due to load ΔP as per the e-logP plot with increase in moisture content (settlement due to the collapse of the soil structure).
H = Thickness of the collapsible layer
e₀ = Initial void ratio

Collapse settlement (S₁) = S₁ + S₂

Solved Example

A building was constructed on collapsible soil and the double oedometer test carried out on the undisturbed sample gave the results shown in Table 1. The thickness of the collapsible layer is 4 m and the average overburden pressure was 60 kPa. Calculate the collapse settlement for an increase in pressure of 40 kPa.

Applied Pressure (kPa)	10	20	40	100	200	400	800
Void ratio at natural moisture content	0.80	0.79	0.78	0.75	0.725	0.68	0.61
Void ratio at soaked condition	0.75	0.71	0.66	0.58	0.51	0.43	0.32

Solution

(1) The first step is to plot the e-log P curve for the two samples as shown below. This has been done using Microsoft Excel. 

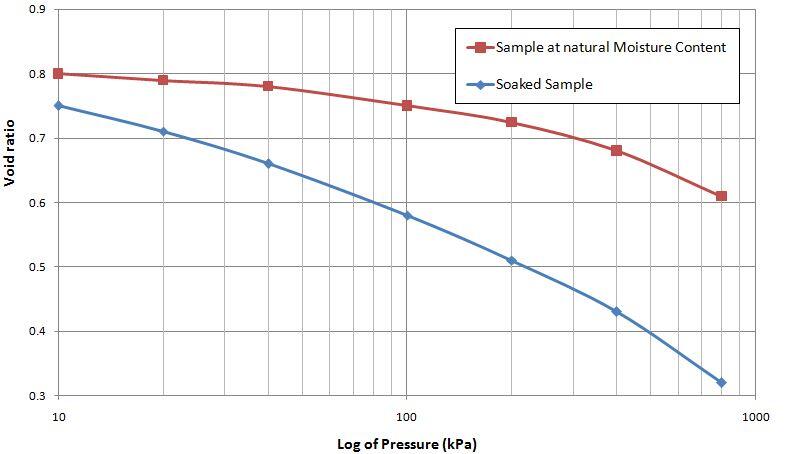
(2) The virgin compression curve is plotted by drawing a line tangential to the soaked sample curve.

(3) After drawing the virgin compression line, the overburden pressure is identified, and for this problem, it is given at 60 kPa. This is traced up to meet the virgin compression line, and this marks the initial void ratio (e₀).

(4) From point e₀, an adjusted moisture curve is plotted to be perfectly parrallel to the natural moisture content curve.

(5) The increment pressure p + ΔP = 60 + 40 = 100 kPa. A vertical line is drawn from the pressure of 100 kPa to meet the soaked sample curve and adjusted moisture curve.

Steps (2) to (5) are shown in Figure 2.

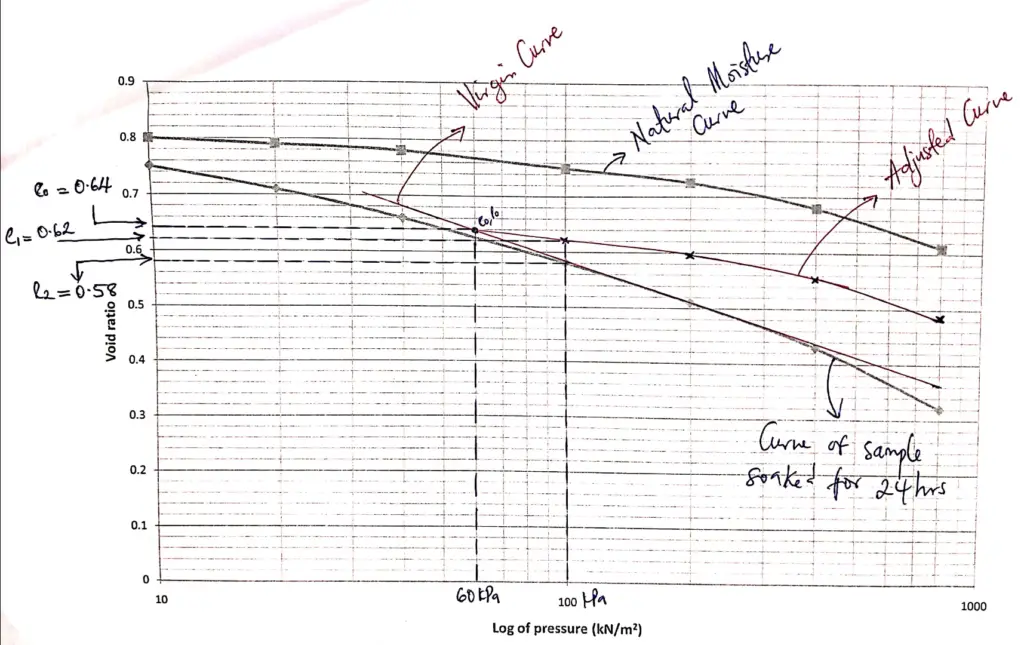
(6) Trace down the points where the pressure increment makes contact with the soaked sample curve and adjusted moisture content curve and identify the associated void ratios e₁ and e₂.

For the problem at hand;
e₀ = 0.64
e₁ = 0.62
e₂ = 0.58

Therefore;
Δe_n = e₀ – e₁ = 0.64 – 0.62 = 0.02
Δe_c = e₁ – e₂ = 0.62 – 0.58 = 0.04

S₁ = Δe_nH /(1 + e₀) = (0.02 x 4)/(1 + 0.64) = 0.0487 m
S₂ = Δe_cH /(1 + e₀) = (0.04 x 4)/(1 + 0.64) = 0.0975 m

The total collapse settlement is therefore given by S₁ + S₂ = 0.0487 + 0.0975 = 0.146 m = 146.2 mm

Methods of Foundation and Construction on Collapsible Soils

(1) Utilising deep foundations such as piles to send the load beyond the collapsible layer.

(2) Chaining the foundation using continuous reinforced ground beams and slab to minimise differential settlement.

(3) In a laboratory study carried out by AlShaba et al.. (2018) at Egypt, iron powder was used to reduce collapse settlement of collapsible soil by about 46% at a mix ratio of 6% of the dry weight of the soil. When the same mixture was compacted, a reduction ratio of about 86.66% was obtained.

(4) Prewetting and compaction of the collapsible soil.

(5) Ayeldeen et al (2016) obtained promising results on improving collapsible soils using biopolymers.

References
[1] Ayeldeen M., Nrgm A., El-Sawwaf M., Kitazume M. (2016): Enhancing the Behaviour of Collapsible Soils using Bioploymers. Journal of Rock Mechanics and Geotechnical Engineering. doi:10.1016/j/jrmge.2016.11.007
[2] AlShaba A.A., Abdelaziz T.M., Ragheb A.M. (2018): Treatment of Collapsible Soils by Mixing with Iron Powder. Elsevier – Alexandria Engineering Journal (57):3737-3745
[3] Behzad Kalantari (2013): Foundations of Collapsible Soils: A Review. Proceedings of the Institute of Civil Engineers Forensic Engineering 166(FE2):57-63
[4] Jennings J.E., and Knight K. (1975): An Additional Settlement of Foundation Due to Collapse Structure of Snady Soils on Wetting. Proceedings to thhe 4th International Conference on Soil Mechanics and Foundation Engineering, Vol 1. Paris
[5] Murthy V.N.S (2012): Textbook of Soil Mechanics and Foundation Engineering (First Edition). CBS Publishers and Distributors Pvt Ltd, India
[6] Owolabi F.A., Ola S.A. (2014): Geotechnical Properties of a Typical Collapsible Soil i South-Western Nigeria. Electronic Journal of Geotechnical Engineering (19):1721-1738