Many engineering vibration problems can be idealised as single degree of freedom systems using mass-spring-dashpot model. In civil engineering, some water tank models and structures can be idealised this way for dynamic analysis such as the water tank shown above.
The ‘dashpot’ is the simplest mathematical element to simulate a viscous damper. The force in the dashpot under dynamic loading is directly proportional to the velocity of the oscillating mass.
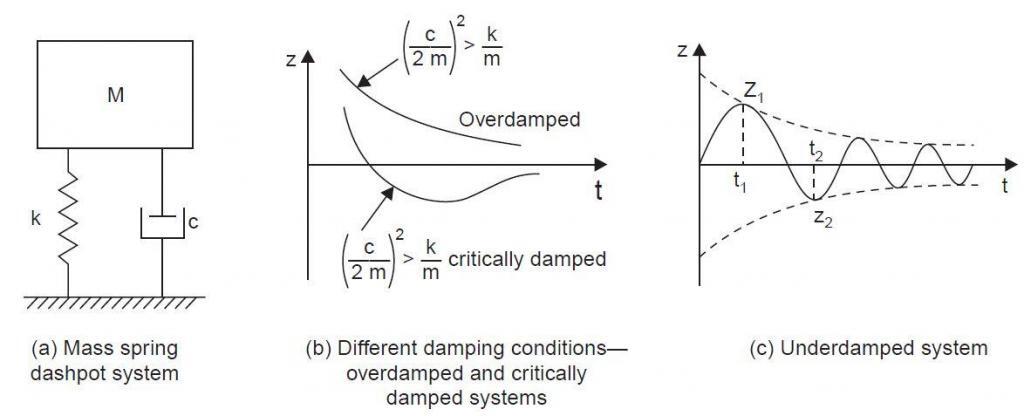
For such structures under free vibration, the equation of motion is;
M.(d2z/dt2) + c(dz/dt) + kz = 0 ——— (1)
Where
M is the mass of the vibrating system
c is the coefficient of viscous damping expressed in force per unit velocity
k is the stiffness of the system
z is the displacement
There are three different type of solutions that can be obtained from equation (1); roots are real and negative, roots are equal, and roots are complex. The solution obtained can be used to describe the nature of damping of the system such as overdamped, underdamped, critically damped etc. For more information consult standard dynamics of structures textbook.
Solved Example
For the SDOF system shown below, plot the displacement time history analysis of the system for the initial conditions;
z = 0.1m, dz/dt = 0, at t = 0
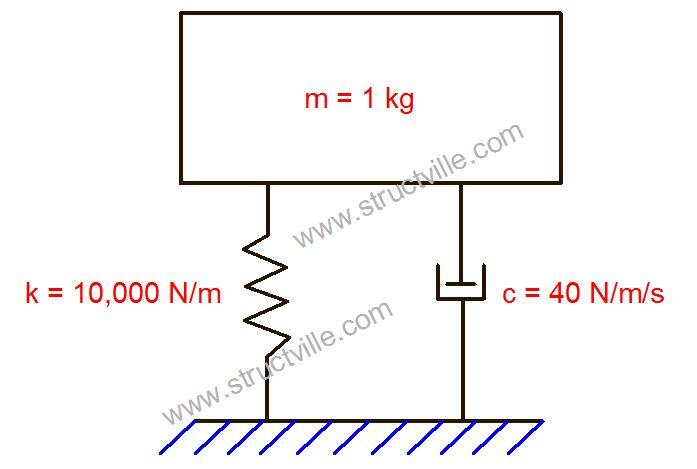
The equation of motion of the system can therefore be given by;
d2z/dt2 + 40(dz/dt) + 10000z = 0
x2 + 40x + 10000 = 0
The solution to the above equation has complex roots given by;
x = -20 ± 97.979i
The general solution to the equation is;
z = e-20t(A cos97.979t + B sin97.979t) —– (2)
From the initial conditions;
z(0) = 0.1 m
0.1 = e-20(0)[A cos97.979(0) + B sin97.979(0)]
0.1 = 1(A + 0)
Therefore A = 0.1
Hence;
z = e-20t(0.1cos97.979t + B sin97.979t) —- (2a)
Differentiating the equation (2a) using product rule;
For the first term of equation (2a);
u = 0.1e-20t; du/dt = -2e-20t
v = cos(97.979t); dv/dt = -97.979 sin(97.979t)
For the second term of equation (2a);
u = Be-20t; du/dt = -20Be-20t
v = sin(97.979t); dv/dt = 97.979 cos(97.979t)
Hence;
dz/dt = -2e-20tcos(97.979t) – 97.979e-20t sin(97.979t) – 20Be-20tsin(97.979t) + 97.979Be-20t cos(97.979t) — (3)
Applying the initial condition dz/dt = 0;
(0) = -2 + 97.979B
Therefore B = 2/97.979 = 0.02041
The equation of motion for the vibrating system is therefore;
z = 0.1e-20t cos(97.979t) + 0.02041e-20t sin(97.979t)
We can verify the solution by using Laplace Transform Method;
d2z/dt2 + 40(dz/dt) + 10000z = 0
z(0) = 0.1; dz/dt(0) = 0
S2ȳ – SX0 – X1 = d2z/dt2
Sȳ – X0 = dz/dt
ȳ = z
(S2ȳ – SX0 – X1) + 40(Sȳ – X0) + 10000ȳ = 0
X0 = 0.1
X1 = 0
(S2ȳ – 0.1S) + 40Sȳ – 4 + 10000ȳ = 0
⇒ S2ȳ + 40Sȳ + 10000ȳ = 4 + 0.1S
⇒ ȳ(S2 + 40S+ 10000) = 4 + 0.1S
Therefore ȳ = (4 + 0.1S)/(S2 + 40S+ 10000)
If we work on the denominator;
S2 + 40S + 202 = -10000 + 202
(S + 20)2 = -9600
What this implies is that;
z = (4 + 0.1S)/[(S + 20)2 + 9600] = [(0.1(S + 20) + 2)]/[(S + 20)2 + 9600]
z = [0.1(S + 20)]/[(S + 20)2 + 9600] + 2/[(S + 20)2 + 9600]
z = 0.1e-20t cos(40√6t) +2/(40√6t)e-20t sin(40√6t)
z = 0.1e-20t cos(97.979t) + 0.02041e-20t sin(97.979t)
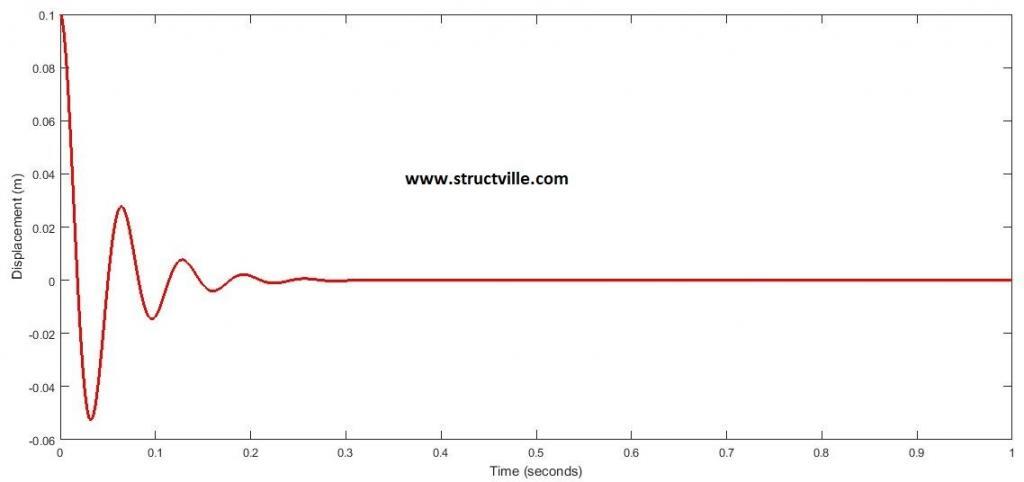
When plotted on MATLAB between 0 and 1 seconds;
t = (0:0.001:1);
k = exp(-20.*t); z = k.*0.1.*cos(97.979.*t) + k.*0.02041.*sin(97.979.*t);
plot(t,z)