Structural dynamics is a field of study that discusses the behaviour of structures subjected to dynamic loads. It encompasses the analysis, design, and evaluation of structures under the influence of various forces and vibrations. While static analysis focuses on the behaviour of structures under constant or slowly varying loads, dynamics of structures explores how structures respond to dynamic loads, which are forces that change rapidly with time.
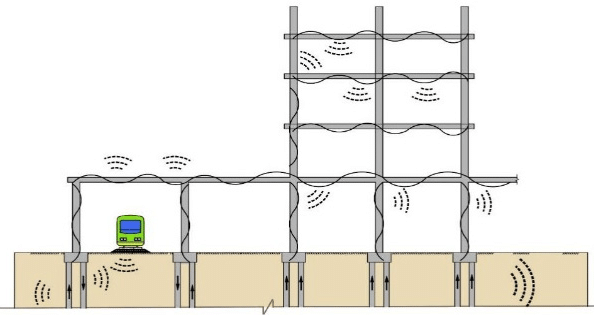
In addition to static loads, a structural system can be subjected to variable (dynamic) loads induced by factors such as wind and wave action, earthquakes, impact, blasts, and vehicular/pedestrian traffic (which causes vibration and fatigue in bridges). Therefore, understanding the dynamic behaviour of structures is important for ensuring the safety and serviceability of structures in scenarios involving:
- Earthquakes: Ground motions induced by earthquakes can cause significant dynamic forces on structures, potentially leading to failure if not properly accounted for in design.
- Wind: Wind loads can create significant dynamic effects, especially on slender structures like tall buildings and suspension bridges.
- Vibrations: Structures subjected to human activity, machinery operation, or traffic can experience vibrations, which can lead to fatigue, discomfort, or even damage if not managed effectively.
- Blast loads: Explosions and other rapid pressure changes can create extremely dynamic forces that need to be considered in the design of structures in specific environments.
This article provides a comprehensive exploration of the key concepts and methodologies involved in the analysis and design of structures subjected to dynamic loads.
Dynamic Analysis
The methods of analysis used for static loads are insufficient to analyze the ‘dynamic’ or ‘time-varying’ loads and their impacts. When compared to the values of displacement that are produced by static loading, the values that are produced by the response of structural members to time-varying loads will likewise be time-varying, and this can result in substantially larger values.
To make the concept of structural dynamics clearer, let us consider a structural element that is subjected to an externally applied load. By considering the equilibrium of applied forces and the internal forces that correspond to those forces, it is always possible to compute the internal stresses and displacements of a structure, regardless of whether the force that is being applied is “static” or “dynamic.”
Assuming that the structure is linearly elastic, the internal forces and the displacements are linearly proportional. If, on the other hand, the force is applied in a dynamic manner, two additional types of internal forces are generated as a consequence. The first of these is referred to as the “inertia forces,” and it is related to the acceleration. The second of these is referred to as the “damping forces,” and it is proportional to the velocity.
In this article, we are going to present a fundamental introduction to the principles of structural dynamics, and how it can be extended to the design of structures.
Importance of Structural Dynamics Analysis
A comprehensive dynamic analysis of structures can reveal the potential for serviceability failures that would be entirely undetectable through a purely static evaluation. For instance, there have been documented cases of oil rigs being decommissioned in relatively calm seas due to the initiation of oscillations that were unacceptably uncomfortable for the crew.
Similarly, electric transmission lines have been known to develop severe dynamic oscillations, referred to as “galloping,” to the extent that the lines made contact. While this phenomenon may not necessarily lead to structural collapse, it undoubtedly constitutes a serviceability failure from the perspective of electricity consumers.
Structures under construction are especially susceptible to dynamic effects. For example, temporary damping measures were deemed necessary for the towers of the Forth Road Bridge in Scotland to mitigate dynamic effects before the installation of the main cables. Even from a purely structural strength perspective, dynamic analysis can be crucial if fatigue is a primary concern.
In such scenarios, it becomes essential to predict not only the magnitude of stresses within the structure but also the frequency at which various stress levels occur. This is because a consistently applied low stress can have a more detrimental fatigue impact than an occasional instance of higher stress.
Characteristics of a Structural Dynamic Problem
A structural dynamic problem differs from a static loading problem in two significant ways. Firstly, the dynamic problem is characterized by its time-varying nature. Since both the loading and the response change over time, a dynamic problem does not have a single solution like a static problem does. Instead, the analyst must determine a series of solutions corresponding to different times of interest in the response history. As a result, dynamic analysis is inherently more complex and time-consuming than static analysis.
The second and more fundamental distinction between static and dynamic problems is illustrated in Figure 2. When a simple beam is subjected to a static load p (as shown in Figure 2a), its internal moments, shears, and deflected shape depend solely on this load and can be calculated using established principles of force equilibrium.
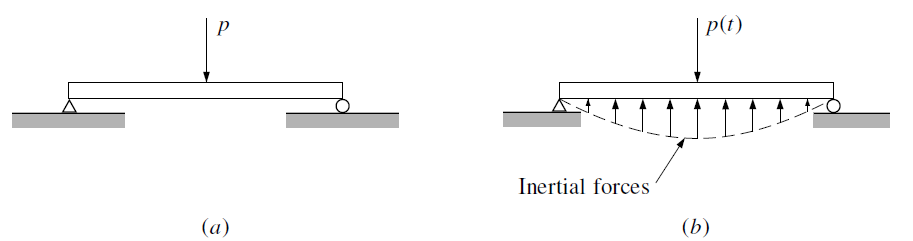
However, when the load p(t) is applied dynamically (as shown in Figure 2b), the resulting beam displacements depend not only on this load but also on inertial forces that resist the accelerations causing them. Consequently, the internal moments and shears in the beam must balance not only the externally applied force p(t) but also the inertial forces resulting from the beam’s accelerations.
Inertial forces, which oppose the accelerations of the structure, are the key distinguishing characteristic of a structural dynamics problem. Generally, if the inertial forces constitute a significant portion of the total load equilibrated by the internal elastic forces of the structure, the dynamic nature of the problem must be considered in its solution.
On the other hand, if the motions are so slow that the inertial forces are negligible, the response analysis for any specific time can be conducted using static structural analysis methods, despite the load and response being time-varying.
Equations of Motion
The mass, stiffness, and damping (energy absorption capability), of a linearly elastic structural system are the basic physical parameters that define the system when it is subjected to external dynamic loading. Consider the ‘dash-pot’ model (representing a simple building with a single storey) that is presented in Figure 3. This model can be used to demonstrate the fundamental idea behind dynamic analysis.
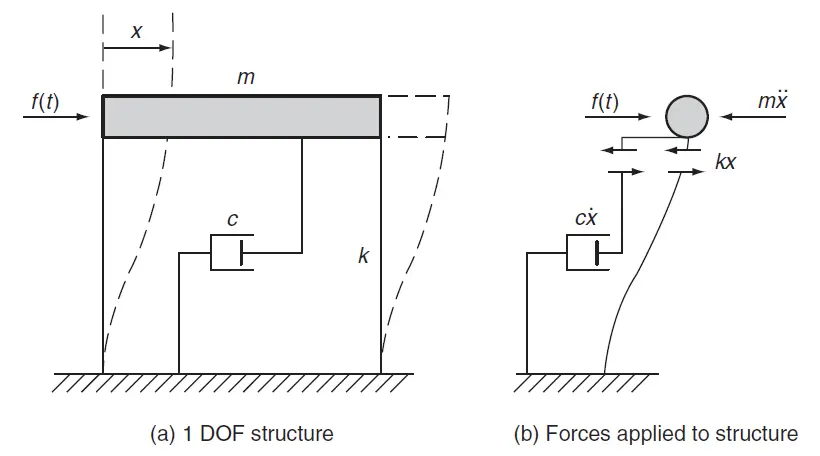
The structure is subjected to a time-varying force denoted by f(t), in which k is the spring constant that links the lateral storey deflection (x) to the storey shear force, and c is a damping coefficient that relates the dashpot’s damping force to the velocity. If it is assumed that all of the mass, m, is located at the beam, then the structure will be considered a single-degree-of-freedom (SDOF) system.
It is possible to write the equation of motion of the system as follows;
mẍ + cẋ + kx = f(t) ——– (1)
Types of Vibration
Free Vibration
While our initial discussion addressed the impact of time-varying loads on structural behaviour (dynamic behaviour), a foundational understanding of vibration in simple structures, independent of dynamic loads, proves most beneficial. This specific type of vibration, termed “free vibration,” arises whenever a structure experiences a disturbance from its state of static equilibrium. The initiation of free vibrations can be attributed to either impulsive events such as a collision or explosion, or to sudden movements in the structure’s support system.
In this case, the system is set to motion and allowed to vibrate in the absence of applied force f(t). Letting f(t) = 0, equation (1) becomes:
mẍ + cẋ + kx = 0 ——– (2)
Dividing equation (2) by the mass m, we have:
ẍ + 2ξωẋ + ω2x = 0 ——– (3)
Where;
2ξω = c/m ——– (4)
ω2 = k/m ——– (5)
The solution to the equation depends on whether the vibration is damped or undamped.
Undamped Free Vibration
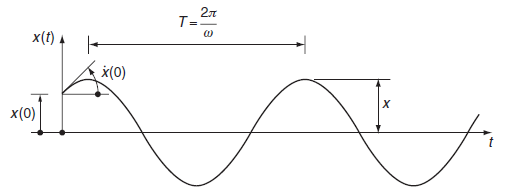
In the absence of not only time-dependent forces, but also any mechanisms for energy dissipation within the vibrating system, the resulting motion can be classified as both free and undamped. Realistically, energy losses due to factors such as friction and air resistance are unavoidable. Therefore, the concept of undamped vibration, while theoretically useful, represents an idealized scenario that disregards these energy-dissipating phenomena. Nevertheless, it remains a valuable tool for theoretical analysis.
In this case, c = 0, and the solution to the equation of motion may be written as:
x = Asinωt + Bcosωt ——– (6)
where ω = √(k/m) is the circular frequency. A and B are constants that can be determined by the initial boundary conditions.
Damped Free Vibration
The phenomenon of damping arises from the inevitable energy loss that occurs during vibration. This lost energy is either dissipated as heat within the structure or radiated outwards, often in the form of sound waves.
Internal friction within the structural materials themselves contributes a portion to this energy loss, with frictional losses at structural joints playing an additional role. While air resistance can also contribute to energy dissipation, it is typically considered a secondary factor.
To model the effects of damping in a simplified manner, engineers often employ a theoretical element known as a “dashpot” system.
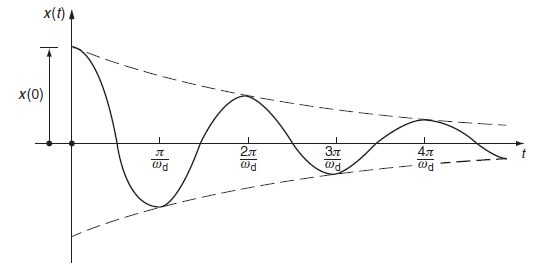
If the system is not subjected to applied force and damping is present, the corresponding solution becomes:
x = A exp(λ1t) + B exp(λ2t) ——– (7)
λ1 = ω[-ξ + √(ξ2 – 1)] ——– (8)
λ2 = ω[-ξ – √(ξ2 – 1)] ——– (9)
The solution of equation (7) changes its form with the value defined as:
ξ = c/2√mk ——– (10)
Forced Vibration
When a structure experiences time-varying loads or continuous disturbances to its supports, the resulting motion is classified as forced vibration. The specific time-dependent influence that triggers this motion is termed excitation. The nature of the forced vibration – its frequency, amplitude, and overall behaviour – is directly tied to the characteristics of the excitation itself.
In essence, the excitation acts as an external “driving force” that dictates the response of the structure. This response can vary significantly depending on the excitation. For instance, a harmonic excitation (a smoothly oscillating force) will lead to a harmonic vibration with the same frequency but potentially a different amplitude. Conversely, a more impulsive excitation, like a sudden impact, can induce a transient vibration with a complex frequency spectrum.
If a structure is subjected to a sinusoidal motion such as a ground acceleration of ẍ = F sinωft, it will oscillate and after some time the motion of the structure will reach a steady state. For example, the equation of motion due to the ground acceleration (from equation (3)) is:
ẍ + 2ξωẋ + ω2x = Fsinωft ——– (11)
The solution to the equation we’ve been examining can be broken down into two key components. The first, known as the complementary solution (represented by equation 6), captures the transient behaviour of the system. If the system experiences any damping, the oscillations associated with this component will gradually diminish over time.
This decay effect eventually leads the system to reach a steady state, where it vibrates with a constant amplitude and frequency. This sustained vibration, termed forced vibration, is solely described by the second part of the solution, the particular solution, expressed as:
x = C1sinωft + C2cosωft ——– (12)
A key observation here is that the forced vibration occurs at the frequency of the excitation force, denoted by ωf, rather than the natural frequency of the structure itself, ω. Essentially, the external force dictates the frequency of the vibration. The term -F/ω² within the particular solution represents the static displacement D caused by the force, essentially accounting for the inertia of the structure.
Now, let’s explore the dynamic response of the structure under varying excitation frequencies relative to its natural frequency (ω):
- Low-Frequency Excitation (ωf/ω > 1): When the applied force oscillates at a frequency significantly lower than the structure’s natural frequency, the response exhibits a characteristic termed quasi-static. In this regime, the system behaves as if it were under a constant load. The response is primarily governed by the stiffness of the structure, and the resulting displacement amplitude closely resembles the static deflection that would occur under a constant force of the same magnitude.
- High-Frequency Excitation (ωf/ω < 1): Conversely, when the excitation frequency is much higher than the natural frequency, the response becomes primarily dependent on the mass of the structure. The displacement amplitude in this case is generally less than the static deflection (D < 1). This is because the structure’s inertia can effectively resist the rapidly oscillating force.
- Resonance (ωf/ω ≈ 1): The most critical scenario arises when the excitation frequency nears the natural frequency of the structure (ωf/ω ≈ 1). Under these conditions, a phenomenon known as resonance occurs. Resonance drastically amplifies the displacement amplitude, potentially leading to catastrophic consequences for the structure. In essence, the external force synchronizes with the structure’s natural tendency to vibrate, causing a dramatic buildup of energy within the system.
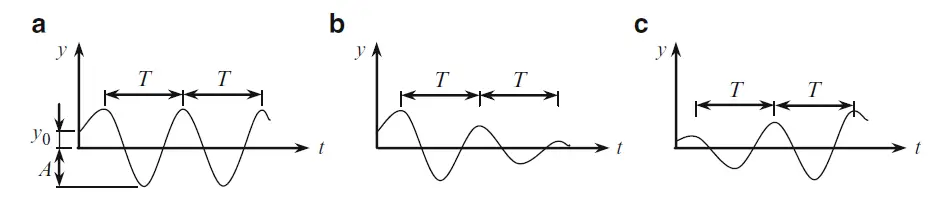
The simplest periodic motion equation can be written as;
y(t) = Asin(ωt + φ0) ——– (13)
where A is the amplitude of vibration, φ0 is the initial phase of vibration, and t is time. This case is presented in Fig. 6a. The initial displacement y0 = Asinφ0 is measured from the static equilibrium position. The number of cycles of oscillation during 2π seconds is referred to as circular (angular or natural) frequency of vibration ω = 2 π/T (radians per second or s-1), T (s) is the period of vibration. Figure 6b, c presents the damped and increased vibration with constant period.
Degrees of Freedom
The concept of degrees of freedom (DOF) plays a crucial role in both statics and structural dynamics. While the definition remains the same – the number of independent parameters that uniquely define the spatial positions of all points in a structure – its interpretation differs subtly between these two fields.
In statics, the DOF is often associated with structures modeled as collections of absolutely rigid discs. Here, a DOF greater than or equal to one signifies a geometrically changeable system. Such a system wouldn’t typically be considered a realistic engineering structure, as real structures exhibit some level of deformation. Conversely, a DOF of zero implies a geometrically unchangeable and statically determinate system – a structure with a unique solution for its equilibrium under applied loads.
However, in structural dynamics, the focus shifts to the deformation of the structural members themselves. A DOF of zero in this context indicates an absolutely rigid body, incapable of any displacement in space. This scenario is purely theoretical, as all real structures exhibit some degree of flexibility.
Furthermore, structures can be broadly classified into two categories based on their DOF:
- Structures with Concentrated Parameters: These represent structures where the distributed mass of individual members can be neglected compared to lumped masses concentrated at specific points along the members.
- Structures with Distributed Parameters: These structures are characterized by a uniform or non-uniform distribution of mass throughout their components. Analyzing these structures often requires more complex mathematical tools compared to those used for concentrated parameter systems.
From mathematical point of view, the difference between the two types of systems is the following: the systems of the first class are described by ordinary differential equations, while the systems of the second class are described by partial differential equations.
Distributed Mass Systems
While the lumped mass model offers a valuable simplification for many structures, it’s important to recognize that all real structures are fundamentally distributed mass systems. This implies that they can be conceptually divided into an infinite number of infinitesimal particles. As a consequence, if a distributed mass system experiences repetitive motion, it theoretically possesses an infinite number of natural frequencies and corresponding mode shapes – unique vibration patterns associated with each frequency.
However, the seemingly overwhelming complexity of analyzing a distributed system can be effectively bridged once its natural frequencies and mode shapes are determined. At this point, the analysis becomes mathematically equivalent to that of a discrete system, where the structure’s behavior is represented by a finite number of lumped masses interconnected by springs or other idealized elements.
The key lies in recognizing that, in practical scenarios, only a limited number of modes, typically those associated with lower frequencies, significantly contribute to the overall dynamic response of the structure. By focusing on these dominant modes, engineers can effectively convert the problem of a distributed mass system into a more manageable discrete system. This approach allows for accurate analysis using computationally efficient methods, enabling engineers to assess the dynamic behavior of real-world structures without getting bogged down by the theoretical infinite nature of distributed systems.
Conclusion
Dynamics of structures considers the interplay between time-varying external forces, internal resistance, and the inherent flexibility of structures. This article has looked into the fundamental concepts of free and forced vibrations, recognizing the crucial role of natural frequencies and damping in shaping a structure’s response.
However, real-world forces and ground motions can be incredibly complex. To accurately predict a structure’s behavior under these conditions, engineers typically rely on numerical analysis techniques. One of the most prevalent methods for solving such complex problems is the finite element method.
The analysis of structures subjected to dynamic loads hinges on the ability to model their behaviour effectively. While lumped mass systems offer a practical approach for many structures, the underlying reality of distributed mass systems with infinite natural frequencies cannot be ignored. The key lies in identifying the dominant modes that significantly influence the dynamic response, allowing us to transform the seemingly intractable distributed system into a more manageable discrete one.
In essence, the lumped mass model serves as a powerful tool for approximating the behavior of complex distributed systems. By strategically selecting the most influential modes, engineers can achieve a high degree of accuracy while maintaining computational tractability. This balance between theoretical completeness and practical feasibility is crucial for ensuring the safety and performance of structures subjected to dynamic loads.
Understanding the dynamics of structures equips engineers with the knowledge to design and build resilient structures that can withstand the challenges of the real world. From earthquakes and windstorms to traffic vibrations and human activity, structures must be able to withstand the complex effects of time-dependent loads without compromising safety, functionality, or serviceability. By mastering the principles of dynamics of structures, engineers can ensure that these structures perform their intended function in harmony with the dynamic forces that surround them.