Comparison of the Force and Displacement Methods of Structural Analysis

The analysis of structures involves the determination of the internal forces (stresses) and deformations (displacements) under various loading conditions. Internal stresses and displacements in frames and other structures are used for the proper design of civil engineering structures.

Two prominent approaches are used in the analysis of statically indeterminate structures: the force method and the displacement method. The force method is also called the method of consistent deformations, while the displacement method is called the stiffness method.

Statically indeterminate structures are structures with additional constraints (redundant), such that the three equations of equilibrium are not sufficient for analysing them. While both the force method and the displacement method aim to achieve the same goal, their underlying principles differ significantly.

The application of the force method and displacement method extends beyond static analysis, encompassing stability and dynamic analysis as well. This discussion centres on a comparison of these two methods, presented in their classical forms.

Comparison of Force and Displacement Methods

Both methodologies necessitate the establishment of primary systems. Furthermore, the generation of bending moment diagrams for unit loads (forces or displacements) is integral to both approaches. In each method, the disparity between the primary system and the original structure is eliminated through the application of a set of well-defined equations.

A comprehensive delineation of the key differences between these methods is presented below.

Primary System

Force method: The primary system is obtained by removing redundant constraints (excess support reactions) from a structure. This makes the structure statically determinate and leaves it with the minimum number of reactions required to achieve static equilibrium.

Displacement method: The primary system is obtained by adding additional constraints (excess support reactions) to the structure. This makes the structure kinematically determinate and leaves it with no unknown rotations and translations.

Primary Unknowns

Force method: The primary unknowns are the forces and moments, representing the removed redundant from the structure. The reactions of the removed redundant are the primary unknowns.

Displacement methods: The primary unknowns are the rotations (slopes) and translations (deflections), representing the additional redundants added to the structure at the points of rotation and translation. The displacements of the added redundants are the primary unknowns.

Number of Primary Unknowns

Force method: Equals the degree of static indeterminacy.

Displacement method: Equals the degree of kinematic indeterminacy.

Way of Obtaining Primary System

Force method: The selection of a primary system for structural analysis is not unique when using the force method. Through strategic selection, all redundant constraints – those exceeding the minimum necessary for stability – can be eliminated and replaced with corresponding reactions (forces and moments) acting at the structure’s supports.

While the choice of which redundant constraints to eliminate is discretionary, the resulting primary system must be statically determinate and stable.

Displacement method: The construction of a primary system in the displacement method demands a unique approach. Each rigid joint within the structure requires the introduction of an additional constraint to prevent any angular rotation. Similarly, for every independent linear displacement (movement in a straight line) that the structure could potentially undergo, an additional constraint must be implemented.

This ensures the primary system represents a set of standard statically indeterminate beams – structures with more unknown forces, moments, and reactions than can be solved for using equilibrium equations alone. This level of indeterminacy necessitates further analysis techniques to determine the complete internal force distribution within the structure.

Canonical Equations

Force Method:
δ₁₁X₁ + δ₁₂X₂ + … + δ_1nX_n + Δ_1p = 0
δ₂₁X₁ + δ₂₂X₂ + … + δ_2nX_n + Δ_2p = 0
. . . . . . . . . . . . = 0

The number of canonical equations is equal to the number of the primary unknowns.

Displacement Method:
k₁₁Z₁ + k₁₂Z₂ + … + k_1nZ_n + K_1p = 0
k₂₁Z₁ + k₂₂Z₂ + … + k_2nZ_n + K_2p = 0
. . . . . . . . . . . . = 0

The number of canonical equations is equal to the number of the primary unknowns.

Meaning of Equations

Force Method: Total displacement in the direction of eliminated constraints caused by the action of all primary unknowns (forces or moments) and applied forces is zero.

Displacement method: The total reaction in the direction of introduced constraints caused by the action of all primary unknowns (linear or angular displacements) and applied forces is zero.

Character of Canonical Equations

Force Method: The nature of the canonical equation using the force method is kinematical: the left part of canonical equations represents displacements.

Displacement Method: The nature of the canonical equation using the displacement equation is statical: the left part of the canonical equations represents reactions.

Matrix of coefficients of canonical equations

Force Method:

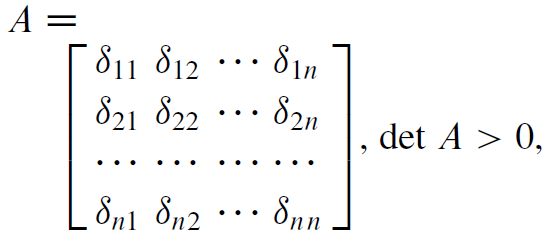
Where A is the flexibility matrix.

Displacement Method:

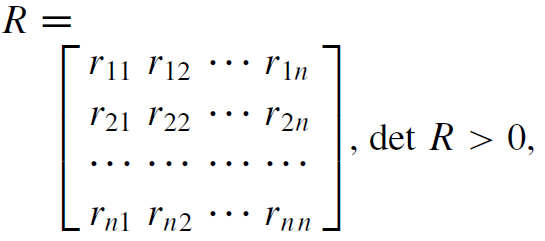
Where R is the stiffness matrix.

Meaning of Unit Coefficients

Force Method: Unit displacement δ_ik presents displacement in the direction of i^th eliminated constraints due to primary unknown (force) X_k = 1

Displacement method: Unit reaction r_ik presents the reaction in the i^th introduced constraints due to primary unknown (displacement) Z_k = 1

Meaning of Free Terms

Force Method: Displacement Δ_iP presents displacement in the direction of i^th eliminated constraint due to applied forces.

Displacement method: Reaction R_iP presents the reaction in the i^th introduced constraint due to applied forces.

A General Overview

The Force Method

The force method, also known as the compatibility method or the method of consistent deformations, focuses on forces acting on a structure as the primary unknowns. The core principle revolves around establishing compatibility conditions that ensure the structure maintains its geometric integrity under load.

Here’s a breakdown of the key steps involved in the force method:

1. Determine the Degree of Statical Indeterminacy: The first step involves calculating the degree of statical indeterminacy (DSI). This value represents the number of redundant constraints (supports or connections) present in the structure. There are established formulas to determine DSI based on the structure’s geometry and support conditions.
2. Choose Redundant Unknowns: Identify the redundant constraints, and select an equal number of unknowns to replace them. These unknowns will typically be the forces or moments acting at the points where the redundant constraints were removed.
3. Construct the Primary Structure: Imagine a statically determinate structure (primary structure) derived from the original structure by eliminating all redundant constraints. This primary structure should be chosen strategically to simplify the analysis while maintaining stability.
4. Replace Eliminated Constraints with Primary Unknowns: At the locations where redundant constraints were removed in the primary structure, introduce the corresponding reactions (forces or moments) as unknowns in the analysis.
5. Form Compatibility Equations: Formulate a set of compatibility equations, equal in number to the degree of statical indeterminacy. These equations relate the displacements of specific points in the structure to the primary unknowns. They ensure that the structure maintains its geometric integrity under load.
6. Solve the System of Equations: Solve the system of equations, formed by the compatibility equations and the equilibrium equations applicable to the primary structure, with respect to the primary unknowns. This step typically involves matrix methods for larger and more complex structures.
7. Determine Remaining Reactions and Analyze the Structure: Once the primary unknowns (reactions due to the eliminated constraints) are determined, all other reactions within the original structure can be calculated using the principles of static equilibrium. With all internal forces and reactions known, a complete analysis of the structure’s behaviour under load can be performed.

Advantages of the Force Method

• Clear Visualization of Forces: The focus on internal forces offers a clear understanding of the load distribution within the structure.
• The force method gives the flexibility to select the most appropriate primary system.
• It gives the user the ability to understand and ”interact” with the structure better.
• The solution yields the direct support reactions of the structure.

Disadvantages of the Force Method

• Complexity for Indeterminate Structures: For indeterminate structures (with more unknowns than equilibrium equations), additional compatibility conditions are needed. This can lead to a more complex and cumbersome solution process.
• Selection of Redundant Forces: Identifying and selecting the appropriate redundant forces (forces that can be removed without affecting the overall equilibrium) can be challenging, especially for complex structures.
• It is more challenging to program on computers.

The Displacement Method

The displacement method, also known as the stiffness method, is the opposite of the force method. Here, the primary unknowns are the displacements (translations and rotations) of specific points within the structure.

The core concept of this method relies on the relationship between applied loads, member stiffness (resistance to deformation), and resulting displacements. Let’s explore the key steps involved:

1. Define the degree of kinematical indeterminacy and construct the primary system of the displacement method.
2. Formulate the canonical equations of the displacement method.
3. Apply successively unit displacements to the primary structure. Construct the corresponding bending moment diagrams.
4. Calculate the main and secondary unit reactions r_ik.
5. Construct the bending moment diagram due to the applied load in the primary system and calculate the free terms RiP of the canonical equations.
6. Solve the system of equations with respect to unknown displacements.
7. Construct the bending moment diagrams.
8. Compute the shear forces using the Schwedler theorem considering each member due to the given loads and end bending moments and construct the corresponding shear diagram.
9. Compute the axial forces from the consideration of the equilibrium of joints of the frame and construct the corresponding axial force diagram
10. Calculate reactions of supports and check them using the equilibrium conditions for an entire structure as a whole or for any separated part.

Advantages of the Displacement Method

• Straightforward for Indeterminate Structures: This method shines when analyzing indeterminate structures. The additional compatibility conditions required in the force method are automatically incorporated through the stiffness matrix.
• Direct Determination of Displacements: Displacements, a crucial design consideration, are directly obtained as the primary unknowns.
• Suitability for Computer Analysis: The stiffness method readily lends itself to computer-aided analysis using software like SAP2000 or ETABS, making it highly efficient for complex structures.

Disadvantages of the Displacement Method

• Less Intuitive for Force Visualization: While internal forces can be determined, the method doesn’t offer the same level of immediate clarity regarding load distribution within the structure compared to the force method.
• Computational Effort for Simple Structures: For simple, determinate structures, the force method produces a larger set of equations compared to the force method.