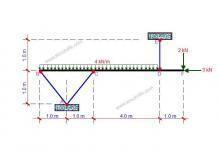
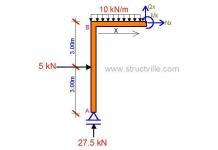
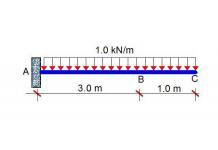
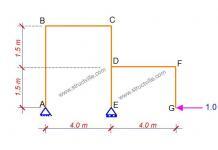
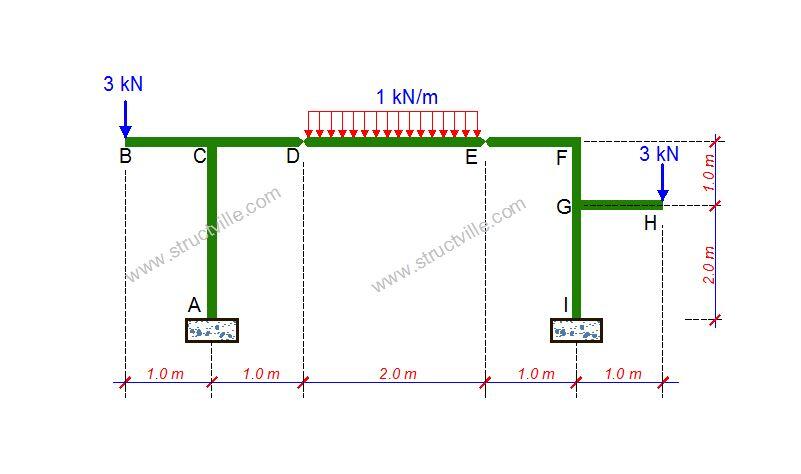
Using the only data available from this picture (which is the crack pattern), what is likely caused failure of this structure?
The structure is a cantilever and we expect the maximum bending moment and shear force to occur at the support (usually taken as the centreline of the column). Predictions can be made on the cause of the failure based on the nature of the crack…
Kindly let us know your view in the comment section. Thank you and God bless you.




Imho maybe torque failure (with not enough/none shear reinforcement bars).
Shear Failure column support they are more spacing
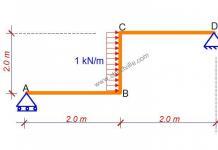
Using “x” and “y” as the vertical plane and “z” as the horizontal plane, there appears to be a high load at the cantilever end in the “z” plane (a beam in the “z” plane) causing torque in the cantilever. The cracks have not propogated through the whole section and are on the outside face of the beam. Not enough vertical bars in the cantilever reo cage.
Diagonal crack failure occur as a result of absent of Z-bar and improper spacing of the links/stirrups /re-Bars which could cause failure at an angle 45degree..
As I can see in the picture there are two cracks, X shape, the wider one is due to not sufficient top rebar in the cantilever and the thin crack is due to not enough stirrups.
Those are shear cracking because of insufficient extra bars providing at that cantilever portion
From the picture, the preventive measure to avoid creation of cracks was overlooked.
Proper concrete mix design ,placement and vibration of concrete is yet to be applied.
Improper design of shear leads to a diagonal compression cracks
This form of cracking is the result of Torsional forces.
The X-shape pattern comes from loading reversal, such as an earthquake.
Termale gradient and no stirrups?
The major cause of fracture of the cantilever beam is insufficient counter weight at the free end of the cantilever beam. Can be redone with same reinforcement and have a parapet wall at the free end.
Insufficient both top bar and shear link.
45 degree cracks are typical of shear failures, produced by bending and / or torsion, and are avoided by placing stirrups and longitudinal steel in the beam faces
I notice a several possibilities that could have caused this failure – even if all elements were correctly sized and placed – the most likely of them all would be
– Firstly – it appears to be fresh concrete
– second -There seemed to be additional loading imposed from new floor above
Third – There is back propping missing from below the cracked cantilever .
Therefore the cause of failure could definitely be additional imposed loads from above & lack of back propping before loading for next level .
taking aside the possible causes due to improper construction and material strength. The x-crack pattern in the cantilever beam is mainly due to the insufficiency of longitudinal and link bars to resist torsional moment in addition to the usually expected shear and bending moment acting on the beam.