Generally, integration is the process of summing up slices or parts in order to find the whole. If dx represents a small displacement or change along the direction x, the process of integration will give a function g(x), the derivative of which △g(x) is equal to the function f(x). This is indicated by the integral sign ∫. Thus, ∫f(x)dx is the summation of the product of f(x) and dx. Numerical integration is a computational (approximate) approach of evaluating definite integrals.
A definite integral is defined by limits (say a and b) and it is given by;
\int_{a}^{b} f(x) \,dxNumerical integration has a lot of applications in engineering such as in the computation of areas, volumes, and surfaces. It also has the advantage of being easily programmable in computer software. In civil engineering, it can be applied in the computation of earthwork volumes such as cut and fill in road construction.
Read Also…
Linear Interpolation for Engineers
For the approximation of definite integrals of the form ∫f(x)dx, the numerical quadrature is normally used. In this method, the function f(x) is normally replaced with an interpolating polynomial p(x) which on integration, obtains an approximate value of the definite integral.
To obtain the numerical solution of functions using the numerical quadrature, the first step is usually to select a distinct set of equally spaced nodes {x0, x1, …., xn} from the interval [a,b]. The smaller the spacing of the nodes or intervals, the more accurate the solution.
Let us assume that Pn is the lagrange interpolating polynomial then we can write;
\\P_n(x) = \sum_{i=0}^{n} f(x_i)L_i(x)
If we integrate Pn excluding its truncation error term over [a ,b], we obtain;
\int_{a}^{b} f(x) \,dx\ =\int_{a}^{b} \sum_{i=0}^{n} f(x_i)L_i(x),dx\\= \sum_{i=0}^{n} a_if(x)Where ai = ∫Li(x)dx for i = 0, 1, 2, 3, … n
There are many methods of approximating the numerical quadrature for numerical integration but we are going to consider the most popular ones which are;
- Trapezoidal Rule, and
- Simpson’s rule
The Trapezoidal Rule for Numerical Integration
The Trapezoidal rule for numerical integration is obtained from considering the integration formula produced by using first Lagrange polynomials with equally spaced intervals. To evaluate ∫f(x)dx within the limits [a, b], let x0 = a and x1 = b. Then h = b – a = x1 – x0
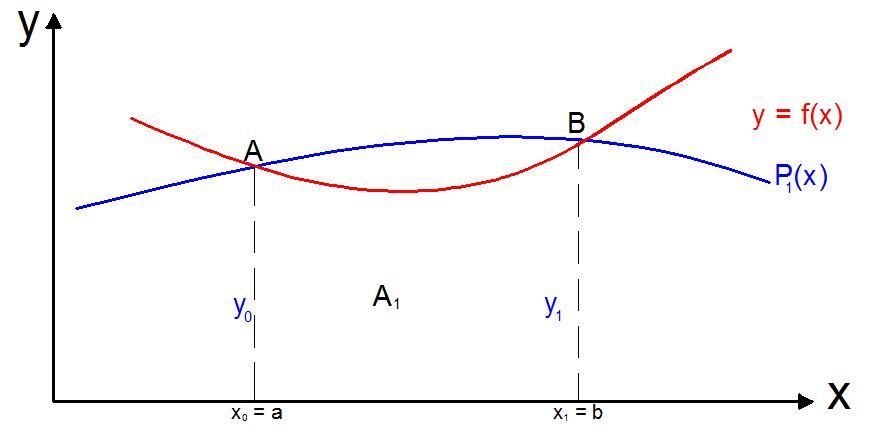
Using the linear Lagrange polynomial;
P1(x)= [(x – x1)/(x0 – x1)]f(x0) + [(x – x0)/(x1 – x0)]f(x1)
Therefore;
\int_{a}^{b} f(x) \,dx\ =\int_{a}^{b}[((x - x_1)/(x_0-x_1))f(x_0) + ((x - x_0)/(x_1-x_0))f(x_1)]dxThe equation above eventually yields;
∫f(x)dx = (x1 – x0)/2[f(x1) + f(x0)}
But (x1 – x0)/2 = h
Hence,
\int_{a}^{b} f(x) \,dx\ = h/2[f(x_1) + f(x_0)] ---- (2.3)
Equation (2.3) is known as the Trapezoidal rule.
It gives good approximation to the value of ∫f(x)dx when the curve of y = f(x) when the interval [a, b] is small, and deviates slightly from the trapezium aABb. However, in a situation when the deviation is violent, i.e. the interval [a, b] is very large, the accuracy in the approximation to the value of ∫f(x)dx can be improved by dividing the interval [a, b] into a larger (even) number of trapezoid of smaller width. This is referred to as the Composite Trapezoidal Rule.
Composite Trapezoidal Rule
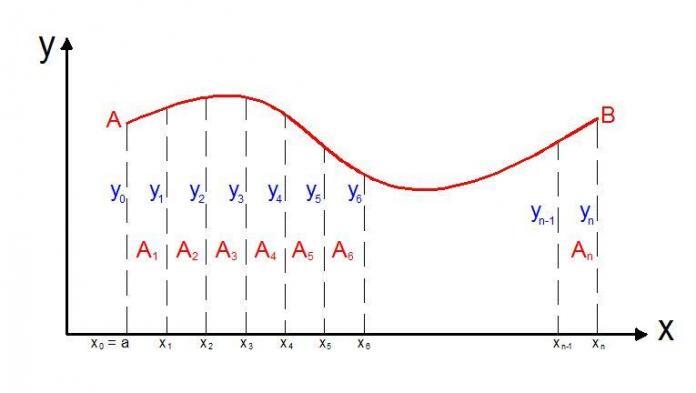
Under the condition that warrants the use of composite trapezoidal rule, we can establish the general formula using the figure below;

The area;
A1 = h/2(y0 + y1)
A2 = h/2(y1 + y2)
A3 = h/2(y2 + y4)
.
.
.
An = h/2 (yn-1 +yn)
Hence
∑Ai = (A1 + A2 + A3 + ⋯ + An)
= h/2 [y0 + yn+ 2(y1 + y2 + y3 + ⋯ + yn-1]
The generalised Trapezoidal Rule can therefore be expressed as;
\int_{a}^{b} f(x) \,dx\ = h/2[f(x_0) + f(x_n) + 2\sum_{i=1}^{n-1}f(x_i)] ---- (2.4)The Simpson’s Rule for Numerical Integration
If we consider the integration formula derived by using the second Lagrange polynomials with equally spaced intervals. If the function f(x) is replaced by an arc of a parabola, and the origin temporarily shifted to a point x = x0 by putting x = X + x0 . We may therefore write the equation of the parabola A0A1A2 as y = y0 + bX + cX2.
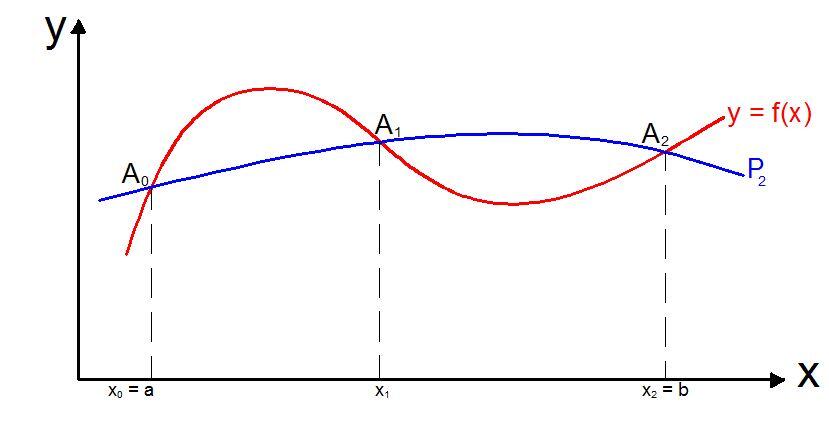
The area of the two adjacent strips under A0A1A2 is approximately;
\int_{0}^{2h} (y_o + bX + cX^2)dx\ = 2h(y_o + bh + 4/3ch^2) Ultimately;
\int_{0}^{2h} (y_o + bX + cX^2)dx\ = h/3(y_o + 4y_1 + y_2) Composite Simpson’s Rule
Similar to Trapezoidal rule, the accuracy of Simpson’s rule can be improved by dividing the interval [a, b] into a larger (even) number of strips of smaller width. Let us evoke fig 6.2, and by considering two successive strips at a time, we can write the expression of Simpson’s formula as thus:
∫f(x)dx = h/3[y0 + 4y1 + y2) + (y2 + 4y3 + y4) + … + (yn-2 + 4yn-1 + yn)
In a more compact form;
∫f(x)dx = h/3[y0 + yn + 2∑even ordinates + 4∑odd ordinates]
Worked Example
Evaluate the integral below using 10 intervals;
\int_{0}^{1} (sinx)dx\ Solution
At 10 intervals, h = 0.1
y0 = f(x0) = sin(0) = 0
y1 = f(x1) = sin(0.1) = 0.0998 (radians)
y2 = f(x2) = sin(0.2) = 0.1986
y3 = f(x3) = sin(0.3) = 0.2955
y4 = f(x4) = sin(0.4) = 0.3894
y5 = f(x5) = sin(0.5) = 0.4794
y6 = f(x6) = sin(0.6) = 0.5646
y7 = f(x7) = sin(0.7) = 0.6442
y8 = f(x8) = sin(0.8) = 0.7173
y9 = f(x9) = sin(0.9) = 0.7833
yn = f(x10) = sin(1.0) = 0.8414
Using the composite Trapezoidal rule;
∫f(x)dx = h/2[y0 + yn+ 2(y1 + y2 + y3 + ⋯ + yn-1]
∫sin(x)dx = 0.1/2[0 + 0.8414 + 2(0.0998 + 0.1986 + 0.2955 + 0.3894 + 0.4794 + 0.5646 + 0.6442 + 0.7173 + 0.7833] = 0.4593
Using the composite Simpson’s rule;
∫f(x)dx = h/3[y0 + yn + 2∑even ordinates + 4∑odd ordinates]
∫sin(x)dx = 0.1/3[0 + 0.84814 + 2∑(0.1986 + 0.3894 + 0.5646 + 0.7173) + 4∑(0.0998 + 0.2955 + 0.4794 + 0.6442 + 0.7833)] = 0.4596
The exact solution
\int_{0}^{1} (sinx)dx\ = 0.459697Therefore, it can be seen that the composite Simpson’s rule approximates better than the composite Trapezoidal rule.