Dynamics of Footbridges | Vibration and Serviceability

Footbridges are susceptible to traffic-induced vibration due to their typical slender nature. Therefore, the serviceability level of pedestrian bridges is influenced by the deformations and vibrations caused by the human traffic on the bridge. In considering the dynamics of footbridges, all types of vibration on the main structure such as vertical and horizontal vibrations, torsional vibrations (which may be alone or coupled with vertical and/or horizontal vibration), should be identified and taken into account.

In studying the dynamics of footbridges, it is important to select and consider the appropriate design situation. This can be influenced by pedestrian traffic admitted on individual footbridges during their design working life, and how access to the bridge will be authorised, regulated, and controlled.

According to [1], the design situations should include:

1. The simultaneous presence of a group of about 8 to 15 persons walking normally as a persistent design situation;
2. The simultaneous presence of streams of pedestrians (significantly more than 15 persons), which could be persistent, transient or accidental depending on boundary conditions, like location of the footbridge in urban or rural areas, the possibility of crowding due to the vicinity of railway and bus stations, schools, important building with public admittance, the relevance of the footbridge itself;
3. Occasional sports, festive or choreographic events, which require specific studies.

Read Also…
Actions on footbridges
Analysis and Design of a Pedestrian Bridge Using Staad Pro

Footbridge-Traffic Interaction

Periodic forces exert by a pedestrian normally walking are;

• vertical, with a frequency ranging between 1 and 3 Hz, and
• horizontal, with a frequency ranging between 0.5 and 1.5 Hz, perfectly synchronised with the vertical ones.

The forces exerted by several persons walking on a footbridge are usually not synchronised and characterised by different frequencies. When the frequency of the forces normally exerted by pedestrians is close to a natural frequency of the deck, it commonly happens that the subjective perception of the bridge oscillation induces the pedestrian to synchronise their steps with the vibrations of the bridge, so that resonance occurs, increasing considerably the response of the bridge.

It is important to note that the number of persons contributing to the resonance of a footbridge is highly random; beyond about 10 persons on the bridge, it is a decreasing function of their number. The resonance is in most cases mainly, but not solely, marked with the fundamental frequency of the bridge. Correlation between forces exerted by pedestrians may increase with movements.

Dynamic models of pedestrian loads

Two separate dynamic models of pedestrian loads for the design of footbridges could be defined:

• a concentrated force (F_n), representing the excitation by a limited group of pedestrians, which should be systematically used for the verification of the comfort criteria;
• a uniformly distributed load (F_s), representing the excitation by a continuous stream of pedestrians, which should be used also where specified, separately from F_n.

Load model F_n, which should be placed in the most adverse position on the bridge deck, consists of one pulsating force (N) with a vertical component;

F_nv = 280k_v(f_v) sin(2πf_vt) —— (1)

and a horizontal component;

F_nh = 70k_h(f_h) sin(2πf_ht) —— (2)

where;
f_v is the natural vertical frequency of the bridge closest to 2 Hz,
f_h is the natural horizontal frequency of the bridge closest to 1 Hz,
t is the time in seconds and,
k_v(f_v) and k_h(f_h) are suitable coefficients, depending on the frequency, given in the figure below;

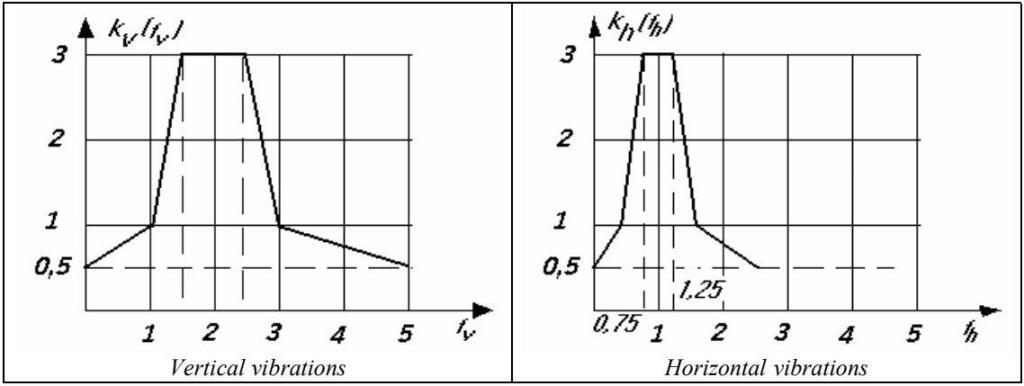
The two components F_n,v and F_n,h should be considered separately.

When inertia effects are evaluated as well as for the calculation of f_v or f_h, F_n should be associated with a static mass equal to 800 kg (if unfavourable), applied at the same location. The uniformly distributed load model F_s, to be applied on the whole deck of the bridge, consists of a uniformly distributed pulsating load (N/m²) with a vertical component;

F_sv = 15k_v(f_v) sin(2πf_vt) —— (3)

and a horizontal component;

F_sh = 4k_h(f_h) sin(2πf_ht) —— (4)

to be considered separately.

When inertia effects are evaluated as well as for the calculation of f_v or f_h, F_s should be associated with a static mass equal to 400 kg/m² (if unfavourable), applied at the same location.

For a particular project, especially for big footbridges, it may be possible to increase the reliability degree of the assessments, by specifying to apply F_s on limited unfavourable areas (e.g. span by span) or with an opposition of phases on successive spans.

Human Comfort Criteria on Footbridges

In order to ensure pedestrian comfort on footbridges, the maximum acceleration of any part of the deck should not exceed;

• 0.7 (m/s²) for vertical vibrations; or
• 0.15 (m/s²) for horizontal vibrations.

The assessment of comfort criteria should be performed when the natural vertical frequency is less than 5 Hz or the horizontal and torsional natural frequencies are less than 2.5 Hz. The assessment of natural frequencies f_v or f_h should take into account the mass of any permanent load. The mass of pedestrians should be taken into account only for very light decks.

The stiffness parameters of the deck should be based on the short term dynamic elastic properties of the structural material and, if significant, of the parapets. When comfort criteria do not seem to be satisfied with a significant margin, it is recommended to make provision in the design for the possible installation of dampers in the structure after its completion.

Evaluation of accelerations shall take into account the damping of the footbridge, through the damping factor ζ referring to the critical damping, or the logarithmic decrement δ, which is equal to 2πζ.

For rather short spans, when calculations are performed using the groups of pedestrians given before, the acceleration can be reduced by multiplying it by;

• k_nv = 1 – e^(-2πnζ) for vertical vibrations or by
• k_nh = 1 – e^(-πnζ) for horizontal vibrations, being

n, equal to 12 times the number of steps necessary to cross the span under consideration.
For a simple span, the design value of the vertical acceleration (m/s²) due to the group of pedestrians may then be taken as equal to;

a_d = 165k_v(f_v) × (1 – e^(-2πnζ))/Mζ —— (5)

M is the total mass of the span, f is the relevant, i.e. the determining, fundamental frequency, and k_v(f_v) is given in Figure 1.

References
[1] Pietro Croce P., Sanpaolesi L. (2005): Bridges – Actions and Load Combinations. In Handbook 4 Design of Bridges (Guide to basis of bridge design related to Eurocodes supplemented by practical examples) Leonardo da Vinci Pilot Project CZ/02/B/F/PP-134007