Design of Timber Beams

Design of flexural members such as timber beams principally involves consideration of the effects of actions such as bending, deflection, vibration, lateral buckling, shear, and bearing. The process of design of such structures is described in Eurocode 5 (EN 1995-1-1:2004), and a design example is shown in this article.

Design Example

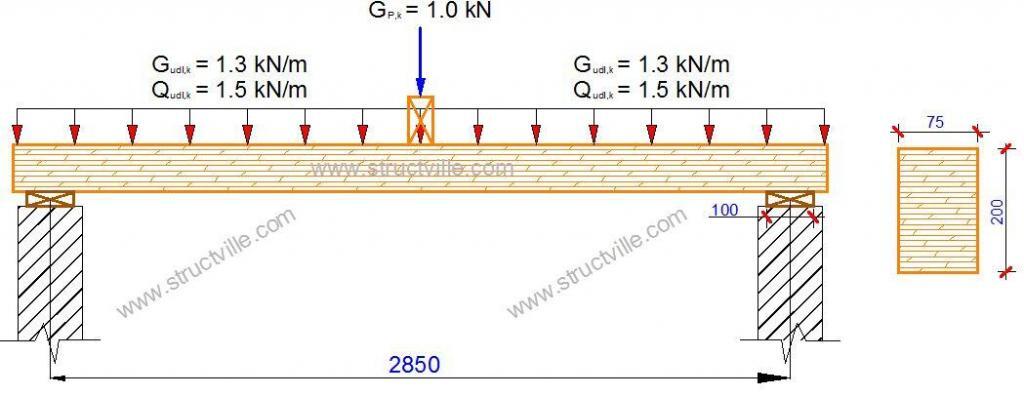
A 75 mm by 200 mm deep sawn timber beam in a domestic residence supports the characteristic loading shown above. The beam has a clear span of 2.75 m, the bearing length has been restricted to 100 mm at each end, is of strength class C24 to BS EN 338:2003, and functions in service class 2 conditions. The beam is laterally restrained against lateral buckling along its length.

Given that;

G_k.udl  = 1.3 kN/m (characteristic uniformly distributed permanent action)
Q_k.udl = 1.5 kN/m (characteristic uniformly distributed medium-term action)
G_k.p = 1.00 kN characteristic point load at mid-span

1. Beam geometric properties
Breadth of the beam b = 75 mm
Depth of the beam h = 200 mm
Clear span of the beam, l_c = 2750 mm
Bearing length of the beam at each end, b_l  = 100 mm
Design span of the beam l = (l_c + l_b) = 2750 + 100 = 2850 = 2.85 m
Section modulus of the beam about the y–y axis, W_y = bh²/6 = (75 × 200²)/6 = 5 × 10⁵ mm³

2. Timber properties
Strength class C24 (BS EN 338:2003, Table 1):
Characteristic bending strength,  f_m.k = 24 N/mm²
Characteristic shear strength,  f_v.k = 2.5 N/mm²
Characteristic bearing strength,  f_c,90,k = 2.5 N/mm²
Fifth-percentile modulus of elasticity parallel to the grain, E_0.05 = 7.4 kN/mm²
Mean modulus of elasticity parallel to the grain, E_0,mean = 11 kN/mm²
Mean shear modulus, G_0,mean = 0.69 kN/mm²
Mean density of the beam timber, ρ_m = 420 kg/m³

3. Partial safety factors
(UKNA to BS EN 1990:2002, Table NA.A1.2(B))) for the ULS
Permanent actions, γ_G.ULS = 1.35
Variable actions, γ_Q.ULS = 1.5

(UKNA to BS EN 1990:2002, Table NA.A1.1 – Category A)
Factor for the quasi-permanent value of the variable action, ψ₂ = 0.3

(UKNA to EC5, Table NA.3)
Material factor for solid timber at the ULS, γ_M = 1.3

4. Actions

(i) ULS
(a) Characteristic self-weight of the beam, G_k,swt
G_k,swt = b · h · g · ρ_m = (0.075 × 0.2 × 9.81 × 420)/1000 = 0.062 kN/m
Design action from the selfweight of the beam, F_d,swt
F_d,swt = γ_G.ULS · G_k.swt  = 1.35 × 0.062 = 0.0837 kN/m

(b) Characteristic permanent action due to the point load, G_k,p
G_k,p = 1.00 kN
Design permanent action due to the point load, F_d.p
F_d,p = γ_G.ULS · G_k.p =  1.35 ×  1.0 = 1.35 kN

(c) Characteristic permanent action due to the UDL, G_k,udl
G_k,udl = 1.3 kN/m
Design action due to the permanent action UDL, F_d,p,udl
F_d,p,udl = γ_G.ULS · G_k.udl  =1.35 x 1.3 = 1.755 kN/m

(d) Characteristic medium-term action due to the UDL, Q_k,udl
Q_k,udl = 1.5 kN/m
Design action due to the variable action UDL, F_d,q,udl
F_d,q,udl = γ_Q.ULS · Q_k.udl = 1.5 × 1.5 =  2.25 kN/m

Total UDL @ ULS = 0.0837 + 1.755 + 2.25 = 4.1 kN/m
Total concentrated action @ ULS = 1.35 kN

5. Modification factors
Factor for medium-duration loading and service class 2, k_mod.med = 0.8 (EC5, Table 3.1)
Size factor for depth greater than 150 mm, k_h = 1.0 (EC5, equation (3.1))
Lateral stability of the beam: k_crit = 1 (EC5, 6.3.3))
Bearing factor k_c,90 = (taken as 1.0) (EC5, clause 6.1.5(2) )
Deformation factor for service class 2, k_def = 0.8 (EC5, Table 3.2)
Load sharing factor, k_sys is not relevant k_sys = 1.0

(6) Bending strength
The design bending moment;

M_d =ql²/8 + PL/4= (4.1 × 2.85²)/8 + (1.35 × 2.85)/4 = 4.162 + 0.96 = 5.122 kNm

Design bending stress, σ_m,y,d = M_d/W_y = (5.122 × 10⁶)/( 5 × 10⁵) = 10.244 N/mm²

Design bending strength, f_m,y,d = (k_mod.med·k_sys·k_h· f_m.k)/γ_M = (0.8 × 1.0 × 1.0 × 24)/1.3 = 14.77 N/mm²

σ_m,y,d < f_m,y,d   Section is okay in bending

(7) Shear Strength
Design shear force V_d = ql/2 + P/2 = (4.1 × 2.85)/2 + (1.35/2) = 6.52 kN

Design shear stress, τ_v.d (EC5, equation (6.60))
τ_v.d = 1.5V_d/bh_ef = (1.5 × 6.52 × 1000)/(75 × 200) = 0.652 N/mm²

Design shear strength,  f_v,d = (k_mod.med·k_sys· f_v.k)/γ_M = (0.8 × 1.0 × 2.5)/1.3 = 1.54 N/mm²

τ_v.d < f_v,d  Section is okay in shear

(8) Bearing Strength
The design bearing force will equal the design shear force in the beam, V_d

Design bearing stress, σ_c,90,d  = V_d/b·l_b = (6.52 × 1000)/(75 x 100) = 0.833 N/mm²

Design bearing strength, (EC5,equation (6.3)))

f_c.90.d = (k_mod.med · k_sys · k_c.90 · f_c.90.k)/ γ_M = (0.8 × 1.0 × 2.5)/1.3 = 1.54 N/mm²

σ_c,90,d  < f_c.90.d  Section is okay in bearing

(9) Deflection

Instantaneous deflection due to permanent actions

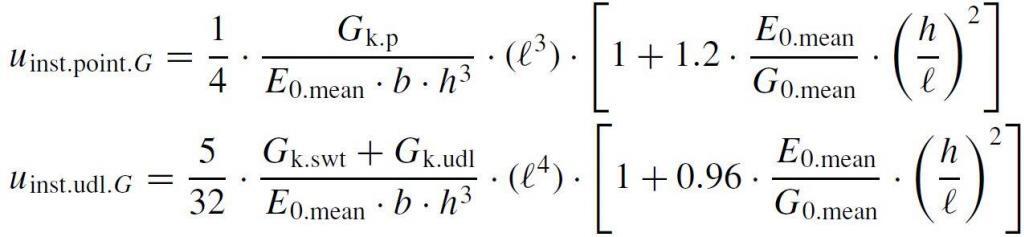
u_inst,point,G = (1/4) × [1/(11 × 75 × 200³)] × 2850³ × [1 + 1.2 × (11/0.69) × (200/2850)²] = 0.959 mm

U_inst,udl,G = (5/32) × [(1.3 × 10^-3 + 0.062 × 10^-3)/(11 × 75 × 200³)] × 2850⁴ × [1 + 0.96 × (11/0.69) × (200/2850)²] = 2.287 mm

U_inst.G = u_inst,point,G + U_inst,udl,G =  0.959 + 2.287 = 3.246 mm

Instantaneous deflection due to variable action

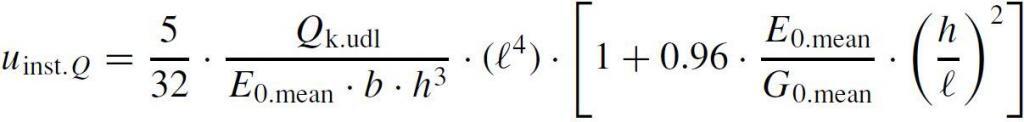
U_inst,Q = (5/32) × [(1.5 × 10^-3)/(11 × 75 × 200³)] × 2850⁴ × [1 + 0.96 × (11/0.69) × (200/2850)²] = 2.519 mm

Combined permanent and variable instantaneous deflection = u_inst = u_inst,G + u_inst,Q = 3.246 + 2.519 = 5.765 mm

Eurocode 5 limit on deflection (Table 7.2, EC5) w_inst = l/300 = 2850/300 = 9.5 mm (u_inst < w_inst Instantaneous deflection is okay)

Final deflection
Final deflection due to permanent actions u_fin,G = u_inst,G (1 + k_def) (Equation 2.3, EC5)
u_fin,G = 3.246  (1 + 0.8) = 5.843 mm

Final deflection due to the variable and quasi-permanent actions,  u_fin,Q = u_inst,Q (1 + ψ₂k_def) (Equation 2.4, EC5)
u_fin,Q = u_inst,Q (1 + ψ₂k_def) = 2.519 (1 + 0.3 × 0.8 ) = 3.12 mm

Final deflection due to the permanent and quasi-permanent actions actions
u_net,fin = u_fin,G + u_fin,Q = 5.843 + 3.12 = 8.963 mm

Deflection limit w_net,fin = l/150 = 2850/150 = 19 mm

The deflection of the beam is satisfactory

To download this design article in PDF format, click HERE.