Design of Timber Joists to EN 1995-1-1:2004

Timber joists are flexural horizontal timber members that are used for framing an open space in a building in order to support a floor or sheathing. They are usually closely spaced (usually between 400 – 800 mm) with the plane of maximum strength positioned vertically.

The spans of the joists are usually supported or intercepted by blockings which may be linear or skewed (staggered). Timber joists transfer the load of the floor to the vertical compression members (such as timber columns) and can be made of solid timber, glulam, or other engineered wood products.

As flexural structural members, the design of timber joists is expected to satisfy the following requirements;

1. Bending
2. Shear
3. Bearing
4. Lateral buckling
5. Deflection, and
6. Vibration

Design Example of Timber Joists

In this article, let us design the timber floor joists for a domestic dwelling using timber of strength class C24 to support a medium-term permanent action of 0.75 kN/m² and a variable (live) load of 1.5 kN/m² given that the:

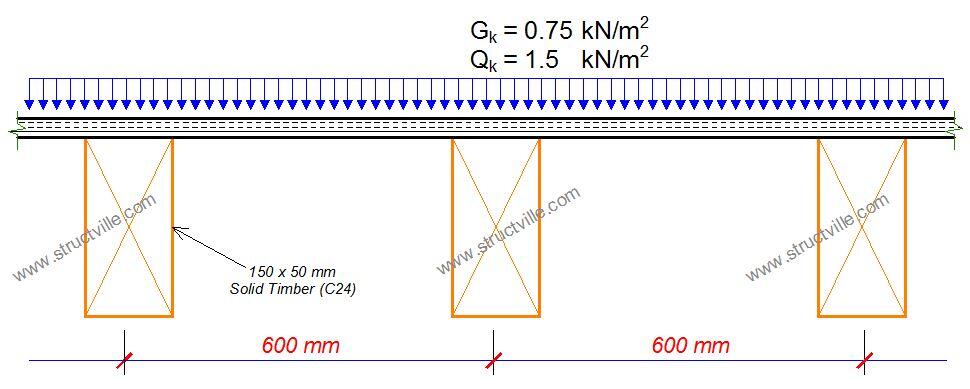
a) floor width, b, is 3.6 m and floor span, l, is 3.0 m
b) joists are spaced at 600 mm centres
c) the bearing length is 100 mm

Self weight of timber = 3.4335 kN/m³ x 0.15m x 0.05m = 0.0257 kN/m
Chaaracteristic permaent action on each joist = 0.75 kN/m² x 0.6m = 0.45 kN/m
Total characteristic permanent action g_k = 0.476 kN/m

Total characteristic variable action q_k = 1.5 kN/m² x 0.6 m = 0.9 kN/m

At ultimate state; p_Ed = 1.35g_k + 1.5q_k = 1.9926 kN/m
At serviceability limit state p_Ed = 1.0g_k + 1.0q_k = 1.376 kN/m

Structural Analysis

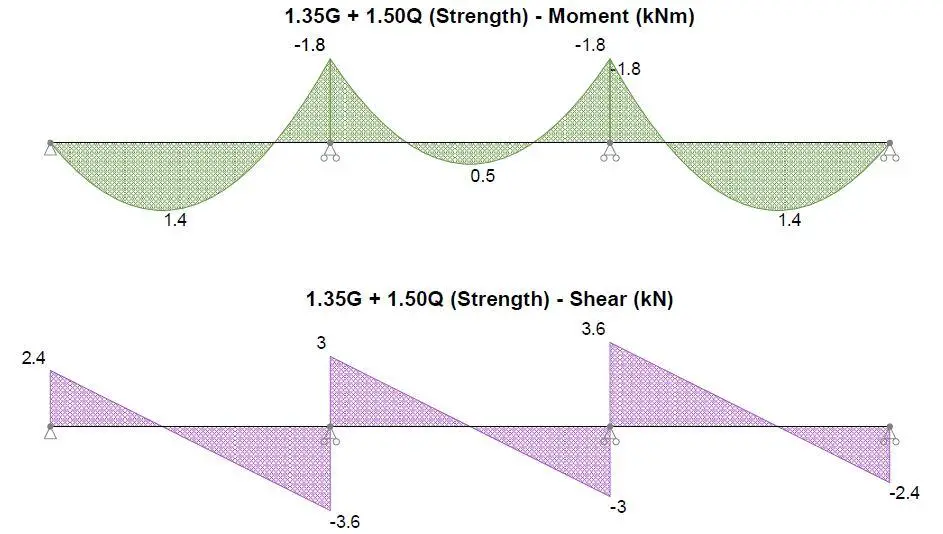
Structural Design
Member – Span 1
The partial factor for material properties and resistances
Partial factor for material properties (Table 2.3 of EN 1995-1-1:2004); γ_M = 1.300

Member details
Load duration (cl.2.3.1.2 of EC5); Medium-term
Service class – (cl.2.3.1.3 of EC5); 2

Timber section details
Number of timber sections in member; N = 1
Breadth of sections; b = 50 mm
Depth of sections; h = 150 mm
Timber strength class – EN 338:2016 Table 1; C24

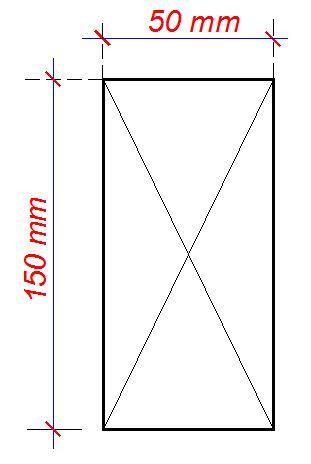
Properties of 50 x 150 mm timber section
Cross-sectional area, A = 7500 mm²
Section modulus, W_y = 187500 mm³
Section modulus, Wz = 62500 mm³
Second moment of area, I_y = 14062500 mm⁴
Second moment of area, I_z = 1562500 mm⁴
Radius of gyration, i_y = 43.3 mm
Radius of gyration, i_z = 14.4 mm

Timber strength class C24
Characteristic bending strength, f_m.k = 24 N/mm²
Characteristic shear strength, f_v.k = 4 N/mm²
Characteristic compression strength parallel to grain, f_c.0.k = 21 N/mm²
Characteristic compression strength perpendicular to grain, f_c.90.k = 2.5 N/mm²
Characteristic tension strength parallel to grain, f_t.0.k = 14.5 N/mm²
Mean modulus of elasticity, E_0.mean = 11000 N/mm²
Fifth percentile modulus of elasticity, E_0.05 = 7400 N/mm²
Shear modulus of elasticity, G_mean = 690 N/mm²
Characteristic density, r_k = 350 kg/m³
Mean density, r_mean = 420 kg/m³

Consider Combination 1 – 1.35G_k + 1.5Q_k (Strength)

Modification factors
Duration of load and moisture content – Table 3.1; k_mod = 0.8
Deformation factor – Table 3.2; k_def = 0.8
Bending stress re-distribution factor – cl.6.1.6(2); k_m = 0.7
Crack factor for shear resistance – cl.6.1.7(2); k_cr = 0.67
Load configuration factor – cl.6.1.5(4); k_c,90 = 1.5
System strength factor – cl.6.6;  k_sys = 1.1

At the start of span

Check compression perpendicular to the grain (cl.6.1.5 of EC5)
Design perpendicular compression – major axis; F_c,y,90,d = 2.394 kN
Effective contact length; L_b,ef = L_b = 100 mm

Design perpendicular compressive stress – exp.6.4; s_c,y,90,d = F_c,y,90,d / (b × L_b,ef) = 0.479 N/mm²
Design perpendicular compressive strength; f_c,y,90,d = k_mod × k_sys × f_c.90.k / γ_M = 1.692 N/mm²
s_c,y,90,d / (k_c,90 × f_c,y,90,d) = 0.189

PASS – Design perpendicular compression strength exceeds design perpendicular compression stress

Check shear force (Section 6.1.7 of EC5)
Design shear force;  F_y,d = 2.394 kN

Design shear stress – exp.6.60; t_y,d = 1.5 × F_y,d / (k_cr × b × h) = 0.714 N/mm²
Design shear strength;  f_v,y,d = k_mod × k_sys × f_v.k / γ_M = 2.708 N/mm²

t_y,d / f_v,y,d = 0.264
PASS – Design shear strength exceeds design shear stress

At the end of span

Check compression perpendicular to the grain – cl.6.1.5
Design perpendicular compression – major axis; F_c,y,90,d = 6.572 kN
Effective contact length; L_b,ef = L_b = 100 mm

Design perpendicular compressive stress – exp.6.4;
s_c,y,90,d = F_c,y,90,d / (b × L_b,ef) = 1.314 N/mm²
Design perpendicular compressive strength;
f_c,y,90,d = k_mod × k_sys × f_c.90.k / γ_M = 1.692 N/mm²

s_c,y,90,d / (k_c,90 f_c,y,90,d) = 0.518
PASS – Design perpendicular compression strength exceeds design perpendicular compression stress

Check shear force – Section 6.1.7
Design shear force; F_y,d = 3.583 kN
Design shear stress – exp.6.60; t_y,d = 1.5 × F_y,d / (k_cr × b × h) = 1.070 N/mm²
Design shear strength; f_v,y,d = k_mod × k_sys × f_v.k / γ_M = 2.708 N/mm²
t_y,d / f_v,y,d = 0.395
PASS – Design shear strength exceeds design shear stress

Check bending moment – Section 6.1.6
Design bending moment; M_y,d = 1.784 kNm
Design bending stress; s_m,y,d = M_y,d / W_y = 9.517 N/mm²
Design bending strength; f_m,y,d = k_mod × k_sys × f_m.k / γ_M = 16.246 N/mm²
s_m,y,d / f_m,y,d = 0.586
PASS – Design bending strength exceeds design bending stress

Serviceability Limit State

Consider Combination 2 – 1.0G_k + 1.0Q_k (Service)
Check y-y axis deflection – Section 7.2
Instantaneous deflection;  d_y = 5.3 mm

Quasi-permanent variable load factor; y₂ = 0.3
Final deflection with creep; d_y,Final = 0.5 × d_y × (1 + k_def) + 0.5 × d_y × (1 + y₂ × k_def) = 8.1 mm

Allowable deflection; d_y,Allowable = L / 250 = 12 mm                
d_y,Final / d_y,Allowable = 0.676

Therefore, the final deflection is acceptable.

It is also typical to check the floor for vibration, but this was not considered in this design.