Free MATLAB Code for Flexural Design of R.C. Sections According to EC2

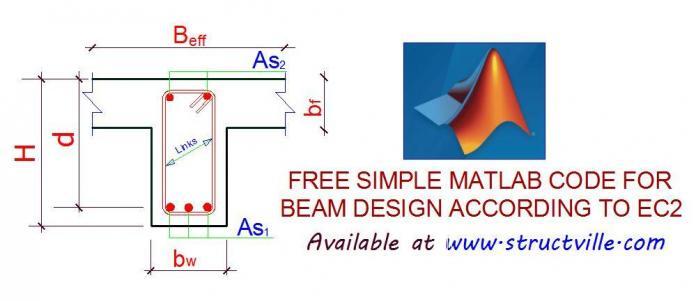
In this post, I am going to present an extremely simplified MATLAB code for carrying out flexural design of reinforced concrete beams (rectangular or flanged) according to Eurocode 2. Before you can use this code, you must carry out your analysis and obtain your design forces and moments. You can just copy the code and paste on your MATLAB script. There are no external functions to be called for the program.

% ANALYSIS AND DESIGN OF RECTANGULAR AND FLANGED BEAMS PER EUROCODE 2
% THIS PROGRAM WILL CALCULATE THE AREA OF REINFORCEMENT REQUIRED, AND ALSO DO THE DEFLECTION VERIFICATION USING THE DEEMED TO SATISFY RULES OF EC2

clc
disp(‘THIS PROFORMA WAS WRITTEN BY O.U.R UBANI’)
disp(‘DOWNLOADED FROM WWW.STRUCTVILLE.COM’)
disp(‘ANALYSIS AND DESIGN OF BEAMS PER EUROCODE 2’)

% INPUT MATERIAL PROPERTIES
Fck = input(‘Enter the grade of concrete (N/mm^2)Fck  = ‘);
Fyk = input(‘Enter the yield strength of steel (N/mm^2)Fyk = ‘);

% INPUT DESIGN MOMENT
MEd = input(‘Enter the ultimate design moment (KNm) MEd = ‘);

% INPUT SECTION AND DESIGN PROPERTIES
h = input(‘Enter the depth of beam (mm)h = ‘);
b = input(‘Enter the effective flange width of the beam (mm)b = ‘);
bw = input(‘Enter the beam width (mm)bw = ‘);
Cc = input(‘Enter concrete cover (mm) = ‘);
dr = input(‘Enter the diameter of reinforcement (mm) = ‘);
dl = input(‘Enter the diameter of links = ‘);

% CALCULATION OF EFFECTIVE DEPTH
disp(‘Effective depth d (mm)’)
d = h-Cc-(dr/2)-dl % Effective depth
disp(‘Depth of reinforcement from the face of concrete’)
do = Cc+dl+(dr/2)

% ANALYSIS FOR INTERNAL STRESSES
ko = 0.167;
k = (MEd*10^6)/(Fck*b*d^2)
if k>ko
disp(‘Since k > ko, Compression reinforcement is required’)
Mcd = (Fck*b*d^2*(k-ko))*10^(-6)
As2 = (Mcd*10^6)/(0.87*Fyk*(d-do))
z = 0.5*d*(1+sqrt(1-3.53*ko))
As1 = ((ko*Fck*b*d^2)/(0.87*Fyk*z))+ As2
else
disp(‘Since k < ko, No Compression reinforcement is required’)
disp(‘Lever arm (la)’)
la = 0.5+sqrt(0.25-0.882*k)
if la>0.95
disp(‘Since la > 0.95,’)
la = 0.95
else
la = 0.5+sqrt(0.25-0.882*k)
end
As1 =(MEd*10^6)/(0.87*Fyk*la*d)
end

% MINIMUM AREA OF STEEL REQUIRED
fctm = 0.3*(Fck^(2/3)) %MEAN TENSILE STRENGTH OF CONCRETE (TABLE 3.1 EC2)
ASmin = 0.26*(fctm/Fyk)*bw*d
if ASmin < 0.0013*bw*d
ASmin = 0.0013*bw*d
end
if As1<ASmin
As1 = ASmin
else
disp(‘Since As1 > Asmin, provide As1 which is the area of steel required’)
end

Asprov1 = input(‘Enter area of tension steel provided (mm^2) = ‘);
Asprov2 = input(‘Enter area of compression steel provided if any (mm^2) = ‘);

% CHECK FOR DEFLECTION

2.0 MATLAB CODE FOR SHEAR DESIGN ACCORDING TO EC2

% SHEAR DESIGN IN EUROCODE 2
clc
disp(‘SHEAR DESIGN ACCORDING TO EC2′)
disp(‘THIS PROFORMA WAS WRITTEN BY O.U.R. UBANI’)

% MATERIALS PROPERTIES
Fck = input(‘Enter the grade of concrete (N/mm^2) = ‘);
Fyk = input(‘Enter the yield strength of steel (N/mm^2) = ‘);

VEd = input(‘Enter the value of shear force at ULS (KN) = ‘);

% SECTION PROPERTIES
h = input(‘Enter the depth of beam (mm) = ‘);
bw = input(‘Enter the beam width (mm) = ‘);
Cc = input(‘Enter concrete cover (mm) = ‘);
dr = input(‘Enter the diameter of reinforcement (mm) = ‘);
dl = input(‘Enter the diameter of links = ‘)
d = h-Cc-(dr/2)-dl % Effective depth
do = Cc+dl+(dr/2)

% CALCULATION OF THE SHEAR CAPACITY OF THE SECTION WITH NO SHEAR REINFORCEMENT
 
Asprov1= input(‘Enter the area of steel provided in the shear zone (mm^2) = ‘) % The reinforcement must exceed the design anchorage length by at least the effective depth
Crd = 0.12
k1= 1+sqrt(200/d)
if k1>2
k1=2
end
disp(‘Reinforcement ratio’)
P1 = (Asprov1/(bw*d))
if P1>0.02
P1 = 0.02
end

% THIS SECTION IS TO BE CONSIDERED IF THERE IS AXIAL FORCE IN THE SECTION
disp(‘Axial force in the section’)
N = input(‘Enter the value of AXIAL FORCE IF ANY(+VE FOR COMP, AND -VE FOR TENSION)(kN) = ‘)
disp(‘Axial stress in the section (Ds)’)
Ds = (N*1000)/(bw*h)
if Ds > (0.2*0.85*Fck)/1.5
Ds = (0.2*0.85*Fck)/1.5
end
k2 = 0.15;
disp(‘Minimum shear stress in the section (N/mm^2)’)
Vmin = 0.035*k1^(1.5)*sqrt(Fck)
disp(‘Concrete resistance shear stress (VRd) (N/mm^2)’)
VRdQ = ((Crd*k1)*(100*P1*Fck)^(1/3)*(bw*d))/1000 % SHEAR FORCE CONTRIBUTION
VRdN = ((k2*Ds)*(bw*d))/1000 % AXIAL FORCE CONTRIBUTION
VRd = VRdQ + VRdN % TOTAL SHEAR RESISTANCE
if VRd < ((Vmin+(k2*Ds))*(b*d))/1000
VRd = ((Vmin+(k2*Ds))*(b*d))/1000
end
if VRd>VEd
disp(‘Since VRd > VEd’)
disp(‘NO SHEAR REINFORCEMENT REQUIRED, PROVIDE NOMINAL LINKS’)
else
if VRd<VEd
disp(‘Since  VRd < VEd’)
disp(‘SHEAR REINFORCEMENT REQUIRED, CALCULATE COMPRESSION STRUT CAPACITY’)
disp(‘Assume strut angle (thetha) = 21.8 deg, cot(thetha)= 2.5’)
thetha = 21.8
V1 = 0.6*(1-(Fck/250))
disp(‘Design compressive strength of concrete (fcd) (N/mm^2)’)
fcd = 0.567*Fck
z = 0.9*d
disp(‘Maximum capacity of compression strut (KN)’)
VRDmax = ((b*z*V1*fcd)/(2.9))/1000
if VRDmax > VEd
disp(‘Since VRDmax > VEd’)
disp(‘OK! Calculate diameter and spacing of links’)
ASMINlinks_to_spacing = ((0.08*sqrt(Fck))/Fyk)*b
ASlinks_to_spacing = (VEd*1000)/(z*0.87*Fyk*2.5)
else
disp(‘Since VRDmax > VEd, it means we need a higher strut angle (beta)’)
disp(‘By calculating the strut angle’)
disp(‘Shear stress at the section (N/mm^2)’)
v = (VEd*1000)/(b*d)
beta = (0.5)*asind((v)/(0.153*Fck*(1-(Fck/250))))
if beta>45
disp(‘Since beta < 45 deg, SECTION INADEQUATE FOR SHEAR, INCREASE DEPTH !!!!!’)
   else
disp(‘The ratio of Area of steel/spacing of links’)
ASlinks_to_spacing = (VEd*1000)/(z*0.87*Fyk*cotd(beta))
end
end
end
Area_of_legs = input(‘Enter the area of number of legs selected = ‘)
Spacing = input(‘Enter the spacing = ‘)
disp(‘CHECK’)
T = Area_of_legs/Spacing
if T > ASlinks_to_spacing
disp(‘Shear reinforcement is ok’)
else
disp(‘Increase area of steel, or reduce spacing’)
end
end  

Like us on Facebook at www.facebook.com/structville 

 



ALSO IN THIS BLOG
Analysis and Design of Continuous R.C. Raker Beam for Stadium using EC2
Two Approaches to the Calculation of Deflection in EC2; Choose a Faster Approach for Yourself