Cables are made from high-strength steel wires that are twisted together. They offer a flexible structural system, which can resist loads only by axial tension. Cables allow engineers to cover very large spans especially in bridges and other suspended structures . Structurally, cables are extremely efficient because they make the most effective use of structural material in that their loads are carried solely through tension through the wire. Therefore, there is no tendency for buckling to occur either from bending or from compressive axial loads.
As load-bearing elements, cables have several unique features. One of them is that vertical loads give rise to horizontal reactions at the support, which, as in case of an arch, is called the thrust. To accommodate the thrust it is necessary to have a supporting structure. It may be a pillar of a bridge, tower, or pylon. Cables are usually employed in suspension bridges, cable-stayed bridges, tower guy wires, roofs, etc.
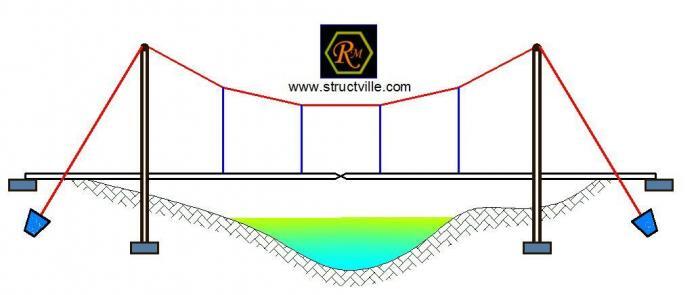
In this post a simplified static model of suspension bridge is presented for the purpose of structural analysis and design (linear first order analysis). The girder has an internal hinge at point G.
GEOMETRICAL PROPERTIES
We know that the thrust at the support of the cables = H = Cx = Dx
We can therefore verify that Cy = Dy = Htanα
You can verify that α = tan-1(4/7) = 29.744°
β = tan-1(3/7) = 23.198°
SUPPORT REACTIONS
∑MB = 0
35Ay + 35Cy – 12Cx + 12Dx – (12 × 352)/2 – (300 × 26) = 0
35Ay + 35Cy – 7350 – 7800 = 0
35Ay + 35(0.5714H) = 15150
35Ay + 20H = 15150 ————– (1)
∑MGL = 0
17.5Ay + 17.5Cy – 12Cx – (12 × 17.52)/2 – (300 × 8.5) + 5H = 0
17.5Ay + 17.5(0.5714H) – 12H + 5H – 1837.5 – 2550 = 0
17.5Ay + 3H = 4387.5 —————– (2)
Solving (1) and (2) simultaneously;
Ay = 172.653 KN; H = 455.537 KN
∑MA = 0
35By + 35Dy – 12Dx + 12Cx – (12 × 352)/2 – (300 × 9) = 0
35By + 35(0.5714H) = 10050
35By + 20H = 10050 ———— (3)
∑MGR = 0
17.5By + 17.5Dy – 12Dx + 5H – (12 × 17.52)/2 = 0
17.5By + 17.5(0.5714H) – 12H + 5H = 1837.5
17.5By + 3H = 1837.5 ————– (4)
Solving (3) and (4) simultaneously;
By = 26.939 KN; H = 455.357 KN
Hence, Cy = Dy = H tanα = 455.357 × 0.5714 = 260.195 KN
ANALYSIS OF THE JOINTS OF THE CABLE
Analysis of support C
∑Fx = 0
-455.357 + FC1 cos29.744 = 0
FC1 = 455.357/cos29.744 = 524.453 KN
Analysis of joint 1
∑Fx = 0
– FC1cosα + F12 cosβ = 0
-524.453cos29.744 + F12 cos23.198 = 0
FC1 = (524.453 × cos29.744)/cos23.198 = 495.411 KN
∑Fy = 0
FC1sinα – F12 sinβ – P1 = 0
(524.453sin29.744) – (495.411sin23.198) – P1 = 0
P1 = 65.047 KN
Analysis of joint 2
∑Fy = 0
– F12 sinβ – P2 = 0
– 495.411sin23.198 – P2 = 0
P2 = 195.147 KN
Therefore, the equivalent loading on the girder is given below;
INTERNAL STRESSES ON GIRDER
Bending Moment on the girder
MA = 0
M1 = (172.635 × 7) – (12 × 72)/2 = 914.445 KNm
ME = (172.635 × 9) – (12 × 92)/2+ (65.047 × 2) = 1197.809 KNm
M2 = (172.635 × 14) – (12 × 142)/2 + (65.047 × 7) – (300 × 5) = 196.219 KNm
MG = (172.635 × 17.5) – (12 × 17.52)/2 + (65.047 × 10.5) – (300 × 8.5) + (195.147 × 3.5) = 0
Coming from the right
MB = 0
M4 = (26.939 × 7) – (12 × 72)/2 = -105.427 KNm
M3 = (26.939 × 14) – (12 × 142)/2 + (65.047 × 7) = -343.525 KNm
MG = (26.939 × 17.5) – (12 × 17.52)/2 + (65.047 × 10.5) + (195.147 × 3.5) = 0
Shear force on the girder
Q1L = 172.635 – (12 × 7) = 88.635 KN
Q1R = 172.635 – (12 × 7) + 65.047 = 153.682 KN
QEL = 172.635 – (12 × 9) + 65.047 = 129.682 KN
QER = 172.635 – (12 × 9) + 65.047 – 300 = -170.318 KN
Q2L = 172.635 – (12 × 14) + 65.047 – 300 = -230.318 KN
Q2R = 172.635 – (12 × 14) + 65.047 – 300 + 195.146 = -35.172 KN
QGL = 172.635 – (12 × 17.5) + 65.047 – 300 + 195.146 = -77.172 KN
Q3R = 172.635 – (12 × 21) + 65.047 – 300 + 195.146 = -119.172 KN
Q3L = 172.635 – (12 × 21) + 65.047 – 300 + 195.146 + 195.146 = 75.974 KN
Q4L = 172.635 – (12 × 28) + 65.047 – 300 + 195.146 + 195.146 = -8.026 KN
Q4R = 172.635 – (12 × 28) + 65.047 – 300 + 195.146 + 195.146 + 65.047 = 57.021 KN
Q4R = 172.635 – (12 × 35) + 65.047 – 300 + 195.146 + 195.146 + 65.047 = -26.939 KN
Obviously, there are no axial forces in the bridge girder.
Thank you so much for visiting STRUCTVILLE.
We love you, and we will like you to like our facebook page on www.facebook.com/structville.
God bless!!










The sign convention you use for your moment diagrams is opposite of most peoples. Most say that positive moment is up as negative moment is down. You chose the same way as the engineers that developed RISA. Its ok,I was just confused ar first. In your example there isnt axial force in a bridge girder but in real life there is. So, you may want to mention you are not considering vehicle stop and go forces nor seismic.
Thank you for your observation. We plot bending moment diagram in the tension zone of the member, so that all positive (sagging) moments are plotted downwards, and all negative (hogging) moments plotted upwards, accurately depicting the tension zone of the material. We do not just follow cartesian coordinates of having positive upwards.
For your second observation, there are axial stresses in real life bridge. This is just a simplified static model. However, any axial load on the structure can be obtained by summing up the axial forces, noting that only the hinged support at A will resist the so-called axial force.
I am uncertain about the assumption of Cy = Dy = Htan(alpha) in the beginning. The reason for this uncertainty is because the external loads onto the superstructure is not symmetrical. (That 300kN located at 9meters from support A)
I clearly understand that at first glance, you might feel that way. But if you look at the structure very well and feel convinced that the horizontal thrusts at the supports of the cable should be equal, then Cy = Dy = Htan(alpha)
• Your skills can be certainly seen by you in the job you write. The arena hopes for even more passionate writers such as you who are not afraid to mention how they feel. All the time follow your heart.
Point Cloud to BIM conversion in USA
ANIMATION SERVICES in USA
BIM Implementation in USA
BIM Project Management in USA
BIM Implementation in USA
BIM Solutions in USA
in actual contruction, at point G is not pinned.. or in considering the design is it necessary to provide pin at the midspan?
It should be hinged at both ends of the girder.
By my calculation, H = 455.357, not 455.537.