Plastic Collapse Analysis of Propped Cantilever Beams

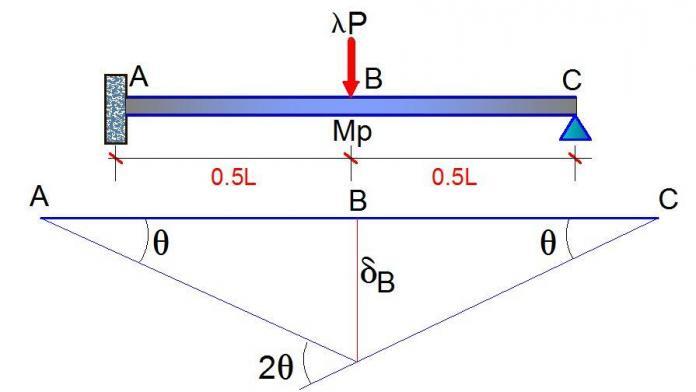
We all know that for a propped cantilever beam, there are two possible locations of plastic hinges – which are at the span (point of maximum moment) and at the fixed support. For the propped cantilever loaded as shown above, the degree is static indeterminacy is 1.

Since the number of possible location of plastic hinges is 2, therefore the number of independent mechanisms is;

P = 2 – 1 = 1 (which is a beam mechanism)

As a result, we are going to carry out our elastic analysis in two stages, so as to determine the load factor at which the beam will form a mechanism and completely collapse. We will start by assuming a value of unity for our load factor (i.e. λ =1.0)

STAGE 1

It is very easy to verify that for the beam loaded as shown above, the fixed end moment at support A = 3PL/16 = (3 × 267 × 8) / 16 = 400.5 KNm

It is also easy to verify that the vertical support reaction at support C (R_C) = 5P/16 = (5 × 267)/16 = 83.4375 KNm

Therefore, the maximum span moment at point B (M_B) = 83.4375 × 4 = 333.75 KNm
The bending moment is as given below.

We can also obtain the vertical deflection at point B by quickly placing a unit load at point B on a basic system of the structure (could be a cantilever or a simply supported beam). Then by combining the shapes from the two states of loading using Vereschagin’s rule, we can obtain the deflection at point B. This is given below.

EIδB = 1/6 × 4 [2(400.5) – 333.75] × 4 = 1246
δ_B = (1246/EI) metres

Therefore, for support A to become plastic, the load factor λA₁= M_P/M_E = 500.625/400.5 = 1.25
Also for section B to become plastic, the load factor λB₁ = M_P/M_E = 500.625/333.75 = 1.5

It is therefore obvious that the first plastic hinge will develop at support A.

Therefore the load at failure of support A = 1.25 × 267 = 333.75 KN
λA₁M_A = 1.25 × 400.5 = 500.625 KN.m
λA₁M_B = 1.25 × 333.75 = 417.1875 KN.m

Deflection of beam at failure of support A = δ_B= (1.25 × 1246)/EI= (1557.5/EI metres)

STAGE 2
Now, support A is assumed to have failed (formed a plastic hinge). We now model it as a real hinge and carry out another elastic analysis.

From statics, the maximum moment of the structure is given by;

PL/4 = ( 267 × 8)/4 = 534 KNm

For section B to become plastic and form a hinge;
λB₂ = (M_P – λA₁M_B)/M_E = (500.625 – 417.1875) / 534 = 0.15625

Therefore, the total load factor at collapse (λ) = λA₁ + λB₂ = 1.25 + 0.15625 = 1.40625

Also, the load at complete collapse of the beam = 1.40625 × 267 = 375.468 KN

The deflection at collapse = δ_B= (1.40625 × 1246) / EI= (1752.1875/EI) metres

Verification using the static method

From geometrical relations, you can observe that δ_B = 4θ

Internal work done due to rotations of the structure at full plastic moment = M_Pθ + M_P(2θ) = 3M_Pθ (the rotation at section C will not count because it is a natural hinge).

External work done by the collapse load = 375.468 × 4θ = 1501.871θ

But External work done = Internal work done;
Therefore, 3M_P θ = 1501.871θ

Therefore, M_P = 1501.871/3 = 500.624 KNm

This shows that the load factor we obtained from our analysis is correct.

For more interesting articles and complete follow up, like our Facebook page;

www.facebook.com/structville