Deflection of Elastic Systems Using Castigliano’s Theorem

Castigliano’s method for calculating deflections is an application of his second theorem, which states that if the strain energy of a linearly elastic structure can be expressed as a function of generalised force P_i then the partial derivative of the strain energy with respect to generalised force gives the generalised displacement w_i in the direction of P_i.

The second theorem of Castigliano is applicable to linearly elastic (Hookean material) structures with constant temperature and unyielding supports.

In general, this is given by;

w_i = ∂U/∂P_i

The strain energy stored in a linear elastic system due to bending is given by;

Solved Example
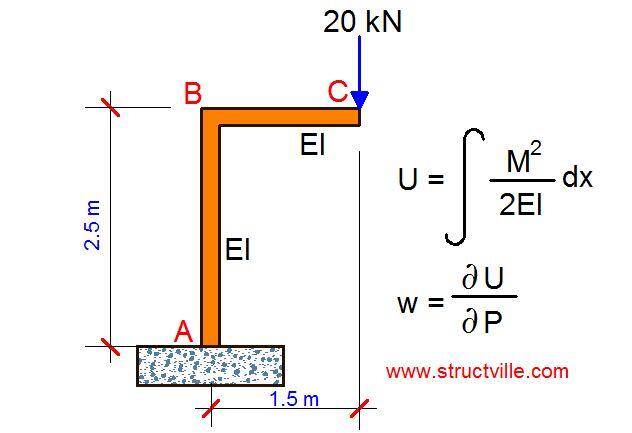
For the frame loaded as shown below, let us find the vertical deflection at point C due to bending using Castigliano’s theorem.

Solution
Section BC
M_x = -20x

U₁ = ∫[(-20x)²/2EI] dx  =  ∫ -400x²/2EI = -400x³/6EI
Knowing that the limit x = 1.5m;
U₁ = 225/EI

Section AB
M_y = (-20 × 1.5m) = 30 kNm

U₂ = ∫[(-30)²/2EI] dy  =  ∫ -900/2EI = -900y/2EI
Knowing that the limit y = 2.5m;
U₂ = 1125/EI

Total strain energy = U₁ + U₂ = (225/EI) + (1125/EI) = 1350/EI

Let the vertical deflection at point C be δ_v

Work done by the externally applied load = 1/2(P × δ)
Work done = Strain energy stored in the system

1/2(20 × δ) = 1350/EI

δv = 135/EI metres