Application of Effective Stress Concept in the Analysis of Cohesive Soils

The application of load on a saturated soil increases the pore water pressure. This sets up a hydraulic gradient which causes the water to flow out of the soil. As water dissipates from the soil mass, the pore water pressures gradually move toward their long-term equilibrium value. This is referred to as consolidation and it is time-dependent. The time taken for consolidation increases with decreasing stiffness and decreasing permeability. In sands and gravel, it is almost instantaneous.

Effective stress condition is used to represent the state when all the excess pore water pressure within the soil mass have dissipated. i.e. the drained state. The reverse is usually referred to as ‘total stress state’. Granular (cohesionless) soils are free-draining, therefore excess pore water pressures created during construction will dissipate so quickly that “effective stress” conditions exist in both the short and long term. Hence the effective angle of internal friction (ø′) is used for any stress analysis involving granular materials.

Clays are naturally complicated materials, and most clay deposits in the world are usually overconsolidated. The analysis of clay soils are usually idealised using;

• Total stress approach (purely cohesive behaviour), or,
• Effective stress approach (purely frictional behaviour)

Frictional behaviour corresponds to conditions where pore water pressures can be defined or assumed and thus allow the strength of the soil to be characterised in terms of effective stress. Cohesive behaviour refers only to the immediate short term when pore water pressures cannot be conveniently defined or assumed. Then, the strength of the soil is represented by the original undrained shear strength, c_u.

In cohesive soils, the change from total stress (undrained conditions) to effective stress (drained conditions) generally occurs over a much longer period of time. The exception being the presence/addition of fine silts/granular material which can greatly reduce the time in which effective stress conditions are reached. During this period, the strength parameters of the cohesive soil may change significantly due to pore water pressures changes induced following the construction of a retaining structure. The change in strength is caused by equalisation of negative pore water pressure in the soil and results in reduced values of cohesion c′ but increased values of angle of internal friction (ø′).

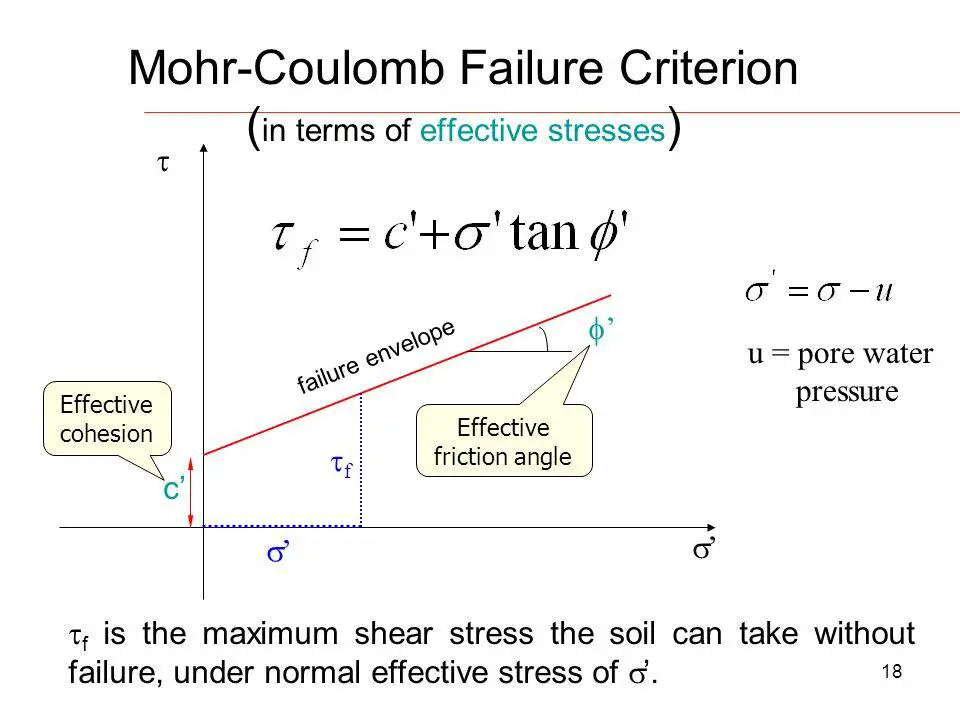
Whilst all cohesive soils are subject to these changes, the effective stress condition is not usually critical when fine silts and naturally consolidated and slightly overconsolidated clays (those with cohesion values of less than about 40kN/m²), are involved, since the change from effective parameters gives an overall increase in soil strength. However, the reverse is true for over-consolidated clays, (those with undrained values in excess of about 40kN/m²). The overall strength will, in most cases, be reduced as the stress condition changes from total to effective because the loss of substantial cohesive strength is not compensated adequately by the increasing angle of internal friction. Hence it is advised that for cohesive soils both short and long-term stress analyses be carried out to determine the more onerous design case.

Typically, long-term calculations are carried out using effective stress parameters – drained analysis. Short-term calculations use total stress parameters – undrained analysis. Traditionally, many generalist engineers have used the cohesion model and total stress procedures. However, any tendency for the pore water to drain will lead to changes in voids ratio and hence the value of undrained cohesion. Voids in soil are not fixed in place; water can move and voids can collapse or expand. Therefore undrained cohesion values are difficult to predict with certainty. In the long term, clays behave as granular soils exhibiting friction and dilation. For this reason, calculations to predict long-term values of pressures are undertaken using the effective stress method.

When using the effective stress method the friction and cohesion can be characterised by the two parameters angle of shearing resistance, φ’ and cohesion intercept in terms of effective stress, c’ (rather than peak angle of shearing resistance, φ’_max). In the absence of test data, BS 8002 recommends values of φ’ that can be used with c’ = 0, and these are given in the Table below.