Depth and Rate of Consolidation Settlement of Foundations

Building foundations founded on saturated clay soils will undergo time-dependent consolidation settlement. This is due to the slow rate of porewater dissipation of clay soils due to their fineness and cohesion. This pore water dissipation is accompanied by volume change in the soil, which results in settlement. It is therefore obvious that such settlement will possess magnitude (depth), and will take some time to complete.

As an engineer or a potential property developer, it is very important to know the depth of settlement that a building foundation will possibly undergo, and the time it will take for such settlement to be complete. This is different from immediate or elastic settlement, which occurs immediately after the foundation is loaded. Immediate settlement occurs in foundations founded on sand or granular materials due to quick pore water dissipation.

In theory, primary consolidation is deemed complete when the pore water pressure is completely dissipated. The subsequent settlement response observed over time is referred to as secondary compression or creep. This phenomenon represents the volume changes within a fine-grained soil triggered by adjustments to its internal structure, the soil fabric, following the completion of primary consolidation.

It is therefore important to distinguish “consolidation” from secondary compression. Consolidation specifically refers to the settlement process that occurs within a soil due to changes in effective stresses, driven by reductions in excess pore water pressure. Notably, the rate of settlement associated with secondary compression is significantly slower compared to that observed during primary consolidation.

If foundation settlement exceeds tolerable limits, the functionality of the structure for its intended purpose may be compromised, potentially leading to a reduced lifespan. Structures may experience settlement uniformly or non-uniformly. The latter scenario, known as differential settlement, often presents the most critical design consideration for engineers.

Magnitude (depth) of Consolidation Settlement

The magnitude and rate of consolidation settlement depend on the engineering properties of the clay soil, the hydraulic conductivity, the stress history of the soil, the drainage conditions (drainage path), applied pressure, and the thickness of the clay layer.

In order to calculate the magnitude of soil consolidation settlement, it is very important to carry out a one-dimensional consolidation test on an undisturbed sample obtained from the site where the building is to be constructed. It is also important to drill a borehole and develop a borehole log to ascertain the thickness and engineering properties of the different soil layers at the site. This will also help in the definition of the drainage conditions of the clay layer.

The one-dimensional consolidation test, pioneered by Terzaghi, is conducted within a specialized apparatus known as a consolidometer (or oedometer). A picture representation of a consolidometer is shown below.

The test involves placing an undisturbed soil specimen collected from the field within a metal ring equipped with porous stones on both the top and bottom faces. Standard specimen dimensions typically consist of a diameter of 64 mm (2.5 inches) and a thickness of 25 mm (1 inch).

Load application on the specimen is achieved through a lever arm, with a micrometre dial gauge recording any resulting compression. To ensure a saturated state throughout the testing process, the specimen is submerged underwater. Each load increment is typically maintained for a 24-hour period.

Following this, the load is conventionally doubled, effectively duplicating the pressure exerted on the specimen. This cycle of load application and compression measurement is then repeated. Upon test completion, the dry weight of the specimen is determined. The experiment leads to the plotting of void ratio versus the log of pressure (e-log P curve) from which a lot of information about the compressibility of the soil can be obtained.

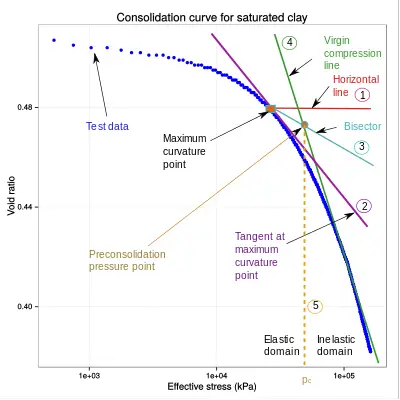
With the information obtained from the analysis of the one-dimensional consolidation test result, it is possible to calculate the probable consolidation settlement of the clay in the field. The equations for the calculation are provided below;

For normally consolidated soils,
S_c = C_cH/(1 + e₀) × log(σ’₀ + ∆σ’)/σ’₀

For overconsolidated clays where σ’₀ + ∆σ is less than or equal to the pre-consolidation pressure σ’c;
Sc = CsH/(1 + e0) × log(σ’0 + ∆σ’)/σ’0

For overconsolidated clays where σ’0 + ∆σ’ is greater than the pre-consolidation pressure σ’_c;
S_c = [C_sH/(1 + e₀) × log(σ’_c /σ’₀)] + C_cH/(1 + e₀) × log(σ’₀ + ∆σ’)/σ’_c

Where;
S_c = Consolidation settlement
C_c = Compression index (C_c = 0.009(L_L – 10)) where L_L is the liquid limit of the clay
C_s = swell index of the clay (C_s = C_c/6)
H = thickness of the clay layer
e0 = initial void ratio of the clay
σ’₀ = effective overburden pressure at the middle of the clay layer
∆σ’ = increment in pressure due to the foundation load
σ’_c = pre-consolidation pressure for overconsolidated soils

Rate of Consolidation Settlement

The rate of consolidation observed in homogeneous soils is directly influenced by a lot of factors such as the soil’s hydraulic conductivity (permeability), its overall thickness, and the designated length of the drainage path. Soil with a lower hydraulic conductivity will experience a longer period for the initial excess porewater drainage, consequently leading to a slower rate of settlement compared to soil with a larger hydraulic conductivity.

During soil consolidation, the length of the drainage path (denoted as H_dr) represents the maximum vertical distance traversed by a pore water particle as it exits the soil stratum. During laboratory consolidation, drainage is usually permitted on both the top and bottom faces of the soil specimen (effectively constituting double drainage conditions), the length of the drainage path, H_dr, is calculated as;

H_dr = H/2

Where H is the thickness of the specimen.

When drainage is permitted only on a single designated face of the soil stratum, the length of the drainage path, H_dr = H. Consequently, shorter drainage paths expedite the consolidation process, leading to the completion of settlement within a reduced timeframe compared to situations with longer drainage paths.

The general equation for one-dimensional consolidation according to Terzaghi is given by;

∂u/∂t = C_v(∂²u/∂z²)

Where C_v is the coefficient of volume change. This equation describes the spatial variation of excess porewater pressure (∆u) with time (t) and depth (z). The solution to the consolidation equation obtained using Fourier series is given by;

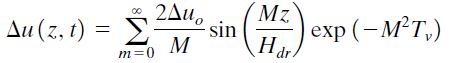
Where T_v = C_vt/H_dr is a non-dimensional parameter known as the time factor.

At the start of the consolidation process (t = 0, T_v = 0), the initial excess porewater pressure, ∆u_o, is equal to the applied vertical stress imposed throughout the entire soil layer. The moment drainage commences, the initial excess porewater pressure instantly reduces to zero at the designated permeable boundaries.

Following the initiation of drainage (t > 0), the total applied vertical stress increment, ∆σ_z, acting at a specific depth, z, is equal to the summation of the vertical effective stress increment, ∆σ’_z, and the remaining excess porewater pressure, ∆u_z. Over an extended period (as time approaches infinity, t → ∞), the excess porewater pressure progressively diminishes to zero. Consequently, the vertical effective stress increment ultimately becomes equivalent to the total vertical stress increment.

We can now define a parameter, U_z, called the degree of consolidation or consolidation ratio, which gives us the amount of consolidation completed at a particular time and depth. This parameter can be expressed mathematically as;

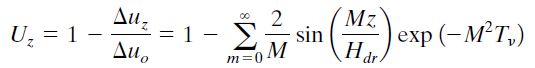
A geotechnical engineer is often concerned with the average degree of consolidation, U, of a whole layer at a particular time rather than the consolidation at a particular depth. The average degree of consolidation can be expressed mathematically from the solution of the one-dimensional consolidation equation as;

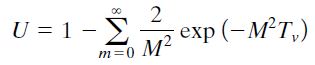
The variation of the average degree of consolidation U with time factor T_v for a uniform and a triangular distribution of excess porewater pressure can be represented using the equations below.

T_v = π/4(U/100)² for U < 60%
T_v = 1.781 – 0.933 log (100 – U) for U ≥60%

The time factors corresponding to 50% and 90% consolidation are often used in interpreting consolidation test results. You should remember that T_v = 0.848 for 90% consolidation, and T_v = 0.197 for 50% consolidation.

The time factor (T_v) provides a useful expression to estimate the settlement in the field from the results of a laboratory consolidation test. If two layers of the same clay have the same degree of consolidation, then their time factors and coefficients of consolidation are the same. Hence,

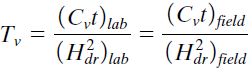
By simplification;

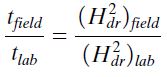
Solved Example

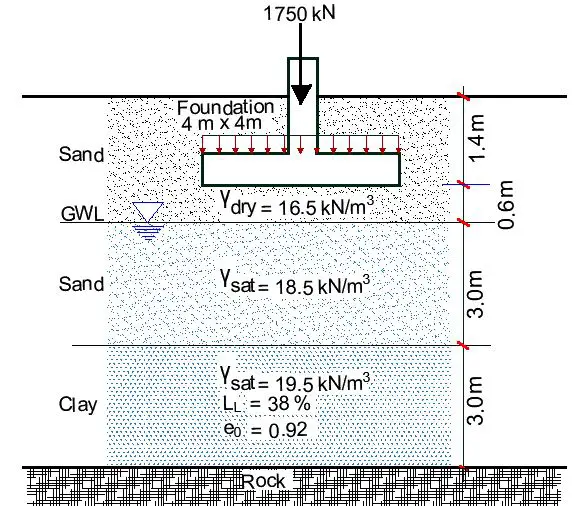
The soil profile shown below is to carry a 4m x 4m square footing carrying a service column load of 1750 kN. The clay is normally consolidated. A sample 25 mm thick, taken from the clay layer 3 m thick, was tested in an oedometer with drainage at the upper and lower boundaries. It took the laboratory sample 6 minutes to reach 50% consolidation.

(a) Calculate the consolidation settlement of the clay layer
(b) How much time would it take the 3m clay layer to achieve 50% and 90% consolidation in the field?

Solution

(a) The magnitude of the settlement

This will be calculated at the middle of the clay layer.

Step 1: Calculate the effective stress in the middle of the clay layer.
σ’₀ = (16.5 × 2) + (18.5 – 9.81) × 3 + (19.5 – 9.81) × 1.5 = 33 + 26.07 + 14.535 = 73.61 kN/m²

Step 2: Calculate the increment in stress in the middle of the clay layer due to the footing load;
Pressure due to footing load = 1750/(4 × 4) = 109.375 kN/m²
The average increment in stress at a depth z = 5.1 m using 1:2 approximate method.
∆σ’ = (109.375 × 4 × 4)/(4 + 5.1)² = 21.13 kN/m²

S_c = C_cH/(1 + e₀) × log(σ’₀ + ∆σ’)/σ’₀

H = 3m
C_c = 0.009(L_L – 10) = 0.009(38 – 10) = 0.252
e₀ = 0.92

S_c = (0.252 × 3)/(1 + 0.92) × log(73.61 + 21.13)/73.61 = 0.0431m = 43.153 mm

(b) The rate of consolidation

Note that in the field, drainage is only in one direction.
Drainage in the lab H_dr,lab = 25mm/2 = 12.5mm = 0.0125m
Drainage in the field, H_dr,field = H = 3m

T₅₀ = c_vt_lab/H_dr,lab² = c_vt_field/H_dr,field²
t_lab/H_dr,lab² = t_field/H_dr,field²

6/0.0125² = t_field/3²

Therefore t_field = 345600 minutes = 240 days

For 90% Degree of Consolidation;

c_vt_field/H_dr,field² = T ∝ U²
So,
t ∝ U²

t₁/t₂ = U₁²/U₂²

240 days/t₂ = 50²/90²

t₂ = 777.6 days

Therefore, it will take the clay layer 240 days to achieve 50% of the total consolidation (21.57 mm settlement). In about 777.6 days (about two years, 1 month and 17 days), 90% of the total settlement will likely be complete (40.637 mm).

Conclusion

Soil consolidation settlement is a time-dependent process influenced by the soil’s hydraulic conductivity (water flow rate), thickness, and drainage conditions. When vertical stress is applied, the soil’s pore water pressure initially increases to resist the stress. Over time, this excess porewater pressure dissipates as water drains, causing the effective stress on the soil to increase and settlement to occur.

This settlement has two parts: primary consolidation, the dominant early stage where excess porewater is squeezed out and the soil densifies, and secondary compression, a much slower later stage where the soil particles themselves gradually rearrange. The time rate of this settlement can be estimated using data obtained by the one-dimensional oedometer test in the laboratory.

With this information, the foundations of buildings and structures can be efficiently designed.