Seismic Slope Stability Design: Newmark Sliding Block Analysis

The Newmark Sliding Block Analysis (Newmark, 1965) is an important tool for evaluating seismic slope stability. This method transcends traditional approaches by directly calculating the displacement a slope might experience during an earthquake. Slope failure is often characterized by the magnitude of this displacement, making the Newmark method a particularly useful and informative technique for seismic stability assessment.

Earthquakes pose a significant threat to earth slopes, potentially triggering landslides and catastrophic failures. To safeguard infrastructure and lives, engineers rely on sophisticated analytical tools to assess slope stability during seismic events. One such prominent method is the Newmark Sliding Block Analysis, a simplified dynamic approach that offers valuable insights into potential seismic displacements.

The Newmark Sliding Block Analysis employs a simplified approach to estimate the accumulated displacement a slope experiences during an earthquake. This method idealizes the ground behaviour as rigid-plastic. In essence, it assumes no relative movement occurs on the slope until the downslope ground acceleration surpasses the critical threshold defined by the slope’s yield acceleration.

Once this threshold is exceeded, the model postulates the slope accelerates downslope at a constant rate, determined by the difference between the ground acceleration and the yield acceleration. By performing a double integration of this constant acceleration over the entire earthquake duration, the analysis estimates the resulting displacement of the slope.

Seismic Loading on Slopes

Earthquakes generate ground motion, characterized by strong accelerations that can destabilize slopes. These accelerations can exceed the inherent shear resistance of the soil within the slope, leading to a loss of equilibrium and triggering a slide. The severity of the threat depends on various factors, including:

• Slope Geometry: Steeper slopes are inherently more susceptible to failure.
• Soil Properties: The strength and frictional characteristics of the soil material significantly influence its resistance to movement.
• Seismic Intensity: The strength and duration of ground shaking play a critical role in determining the potential for slope failure.

The Newmark Sliding Block Approach

The Newmark Sliding Block Analysis simplifies a slope into a rigid block resting on a soil foundation. This idealized model assumes the slope remains stable until the ground acceleration (a_g) exceeds a critical value known as the yield acceleration (a_y). The yield acceleration represents the threshold at which the resisting forces within the soil are overcome, and the block begins to slide downslope.

The core concept of the Newmark method lies in calculating the accumulated displacement of the sliding block throughout the earthquake. This displacement is estimated by integrating the difference between the ground acceleration and the yield acceleration over time. The analysis typically employs a time-history record of ground acceleration from a seismic event or a representative design earthquake scenario.

The core concept of the analysis hinges on an analogy. As a slope undergoes failure, the displaced soil mass can be visualized as a rigid block sliding down an inclined plane. By establishing force equilibrium for this idealized block, Newmark’s method proposes a framework for predicting the permanent displacement a slope might experience under the influence of ground acceleration. This approach provides valuable insights into the potential behaviour of slopes during seismic events, aiding engineers in safeguarding infrastructure and lives.

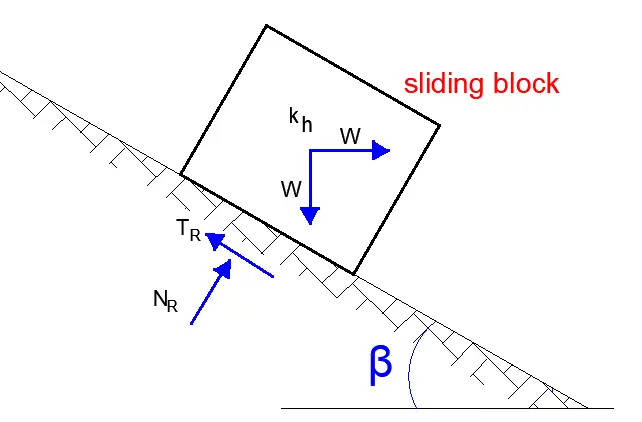
Consider the force equilibrium of the block shown in the image above. The block is subjected to a horizontal inertial force, k_hW. Assuming the resistance to the sliding is only because of friction, and there is no cohesion, the factor of safety for the sliding is:

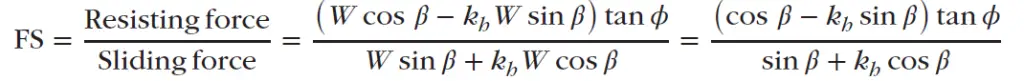
where:
𝜙 = friction angle,
𝛽 = inclination angle of the plane, and
k_h = horizontal acceleration coefficient

The critical condition for sliding is FS = 1.0, which corresponds to a critical horizontal acceleration coefficient called the yield acceleration coefficient. The yield acceleration coefficient, ky, can be obtained by setting FS = 1.0 in the Equation above and solving for k_y:

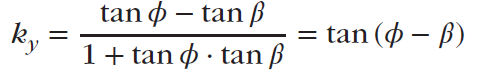
Accordingly, the yield acceleration is defined by:

a_y = k_yg

Displacement occurs when the force equilibrium is not satisfied, that is, when the actual acceleration exceeds the yield acceleration. By analyzing the acceleration, velocity, displacement, and duration of four earthquakes, Newmark (1965) proposed a conservative upper-bound permanent displacement, u_max:

u_max = (v² max′/2a_y) ⋅ (a_max/a_y)

where:
v_max = maximum velocity of ground motion,
a_max = peak horizontal ground acceleration.

Solved Example

Ground motion data from the 2019 Ridgecrest, California, earthquake revealed a peak ground acceleration (PGA) of 0.47 g and a peak ground velocity (PGV) of 55.1 cm/sec. An adjacent earth embankment has the following parameters:

Height = 10 meters,
Slope inclination = 25 degrees
Unit weight of soil = 18 kN/m³
Cohesion of soil = 26 kN/m²,
Internal friction angle = 31 degrees.

Evaluate the permanent displacement of the slope using the Newmark sliding block method.

Solution
The problem statement gives:
Maximum velocity of ground motion: v_max = 55.1 cm/sec
Peak horizontal ground acceleration: a_max = 0.47g

The yield acceleration coefficient can be approximated using Equation the equation;
k_y = tan(𝜙 − 𝛽)
where: internal friction angle 𝜙 = 31^∘, and the slope angle 𝛽 = 25^∘.

So:
k_y = tan(𝜙 − 𝛽) = tan(31 − 25) = 0.105
So a_y = 0.105 g

The upper-bound permanent displacement of the slope is:
u_max = (v²_max′/2a_y) ⋅ (a_max/a_y) = [(55.1²/(2 × 0.105 × 981)] × (0.47g/0.105g) = 65.966 cm

Limitations of the Newmark Model

The Newmark block model might not be entirely accurate when analyzing slopes reinforced with elastic elements like geotextiles or ground anchors. A key assumption of the Newmark model is that a slope’s resistance to movement stays the same regardless of how far it moves. However, elastic support elements like anchors or reinforcement actually become stronger as they stretch further, which the Newmark model doesn’t account for.

Several advancements have been developed to address the limitations of the basic Newmark method:

• Deformable Block Models: These models incorporate some degree of flexibility within the sliding block, providing a more realistic representation of slope behaviour.
• Strength Dissipation: More sophisticated methods account for the potential decrease in soil strength during seismic loading, offering a more accurate assessment of slope stability.
• Multi-Block Models: These models divide the slope into multiple blocks, allowing for a more sophisticated consideration of variations in soil properties and internal deformations.

Applications of Newmark Sliding Block Analysis

The Newmark Sliding Block Analysis serves as a valuable tool in various seismic design applications:

• Preliminary Screening: The method provides a quick and efficient means to assess the overall stability of a slope subjected to seismic loading.
• Design Parameter Selection: The analysis aids in selecting design parameters like reinforcement requirements for slopes based on the estimated seismic displacements.
• Comparison of Scenarios: By analyzing different earthquake scenarios, engineers can evaluate the sensitivity of a slope to varying levels of seismic intensity.

Conclusion

The Newmark Sliding Block Analysis stands as a cornerstone methodology in seismic slope stability assessment. While acknowledging its limitations, engineers leverage its simplicity and effectiveness to gain valuable insights into potential seismic displacements. As the field of geotechnical engineering continues to evolve, advancements in analytical tools and a deeper understanding of soil behaviour will further refine our ability to safeguard slopes from the perils of earthquakes.