The lateral load resistance and stability of buildings get increasingly important as the height of the building increases. Gravity loads on buildings can be said to vary linearly with height. In a fairly regular building, the increment in axial load in columns can be said to increase linearly as you move from the roof to the ground floor. On the other hand, lateral loads are quite variable and increase rapidly with height [1].
For example, under a uniform wind load, the overturning moment at the base varies in proportion to the square of the height of the building, while the lateral deflection varies as the fourth power. However, wind load distribution actually increases with height, and this gives rise to a greater base bending moment [2].
In actual sense, the pressure exerted by wind on a building are not steady, but dynamic and highly fluctuating [3]. This fluctuating pressure could bring severe damage to the building other than the wind force itself, especially due to fatigue [4].

For structural designs, one of the ways to safely assume wind pressures is through the quasi-steady assumption in which the building is subjected to a steady lateral wind force. This is the approach reported in many codes of practice for the loading of buildings. It is the duty of the structural engineer to select the structural system that will resist the gravity and lateral actions, and at the same time satisfy serviceability requirements of the structure, especially in terms of occupancy comfort due to vibration and sway.
One of the main tasks when designing high-rise buildings is to give the structure the ability to absorb the horizontal forces, and to transmit the resulting moment into the foundation [2, 4]. The loads acting on a tall building can be simply divided into vertical and horizontal actions.
The vertical loads are the weight of the building, imposed load and snow loads (where applicable). The horizontal loads are wind loads, seismic response, unintended inclinations/tilt, impact forces, blasts etc.
The vertical loads are taken up by the bearing walls, columns or towers and are led to the foundations. The loads occurring from the wind are first taken by the façades and are then further distributed to the slabs [6]. The floor slabs act as diaphragms and are often considered to be stiff in their plane and deformations in its plane are usually disregarded. The slabs are connected to the stabilising units, such as shear walls, cores, or stabilising columns.
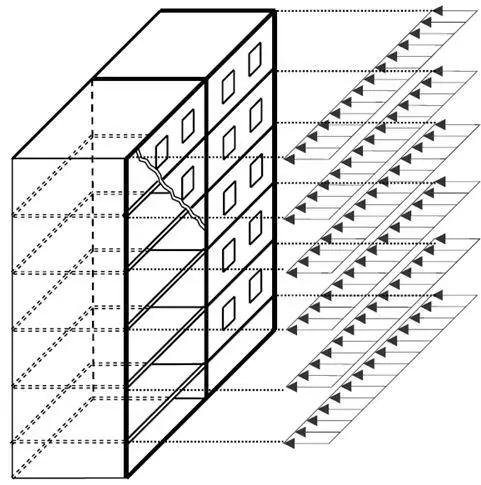
If the façade which takes the wind load is supported by the floor slabs, then the floor slabs will be subjected to a distributed load. However, when the facades have columns attached directly to them, the loads are first transferred to the columns resulting in concentrated loads on the floor slabs. The stress distributions have to be dealt with through careful planning of how the slabs and the facade are connected.
Floor slabs are often considered to be stiff, and the horizontal load distribution through the building is due to the stiffness of the different stabilising components. If the floor slab is not stiff enough, or slip occurs in joints between slab elements in the same plane, then the displacement of the floor slab will not be the same along the loaded side of the floor slab. Stress distribution in floors depends on both loads and supports [6].
The floor of a tall building is supported by the stabilising units through a shear force distributed along the width of the wall. The walls are subjected to both bending and shear deformations but in low robust walls the bending contribution is negligible. If slender units are used for stabilising then bending mainly occurs and shear deformation is negligible.
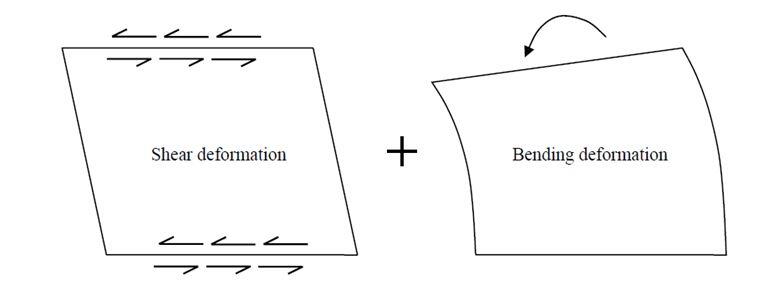
Based on holistic considerations, shear walls become more slender in taller structures, even though shear walls are usually considered as low and robust on each floor. It is, therefore, necessary to consider both bending and shear deformations when designing tall buildings. The deformation from bending is curved in the opposite direction to the shear deformation. The deformation from shear is due to the shear forces applied through the floor slabs in each storey. As the loads accumulate and increase through the building the largest singular deformation occurs at the first floor for the shear contribution.
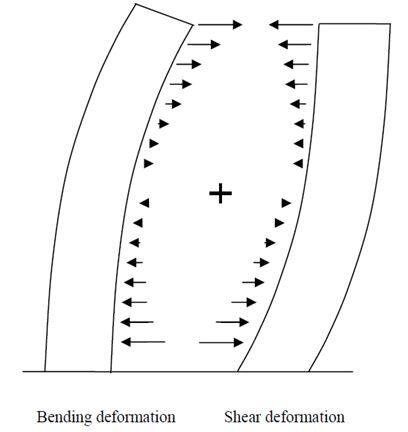
Bending and shear deformation of a shear wall [6]
References
[1] Bungale S. T. (2010): Reinforced Concrete Design of Tall Buildings. CRC Press, Taylor and Francis Group
[2] Hallebrand E., and Jakobsson W. (2016): Structural design of high-rise buildings. M.Sc thesis presented to the Department of Construction Sciences (Division of structural mechanics), Lund University, Sweden
[3] Nizamani J., Thang B.C., Hiader B., and Sharrif M. (2018): Wind load effects on high rise buildings Peninsular Malaysia. IOP Conference Series: Earth and Environmental Science 140(2018)01215
[4] Sandelin C. and Bujadev E. (2013): The stabilization of high-rise buildings: An evaluation of the tubed mega frame concept. M.Sc Dissertation submitted to the Department of Engineering Science, Applied Mechanics, Civil Engineering Uppsala University.
[5] https://www.theb1m.com/video/how-tall-buildings-tame-the-wind Assessed on the 23rd of October, 2020
[6] Gustaffson D., and Hehir J. (2005): Stability of tall buildings. M.Sc thesis submitted to the Department of Civil and Environmental Engineering, Chalmers University of Technology, Sweden










