Structural Analysis Example: Arch Bridges

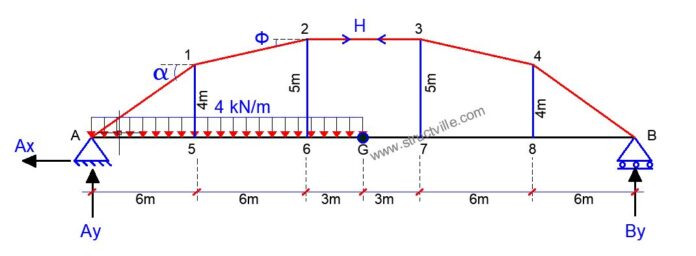
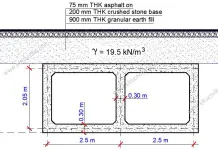
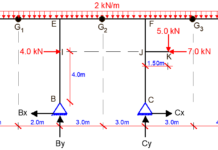
For the given arch bridge loaded, as shown above, determine the following;

(a) The support reactions
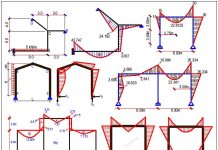
(b) The bending moment diagram of the girder
(c) The shear force diagram of the girder
(d) The axial force diagram of the girder

Support Reactions

∑M_B = 0
30A_y – (4 × 15) × (15/2 + 15) = 0
30A_y – 1350 = 0
Therefore; A_y = 1350/30 = 45 kN

∑M_G^L= 0
15A_y – (4 × 15²)/2 + 5H = 0
15(45) + 5H = 0
Therefore; H = -225/5 = -45 kN

∑M_A = 0
30B_y – (4 × 15²)/2 = 0
30B_y – 450 = 0
Therefore; B_y = 450/30 = 15 kN

∑M_G^R= 0
15B_y + 5H = 0
15(15) + 5H = 0
Therefore; H = -225/5 = -45 kN

Analysis of the Joints

Joint 2

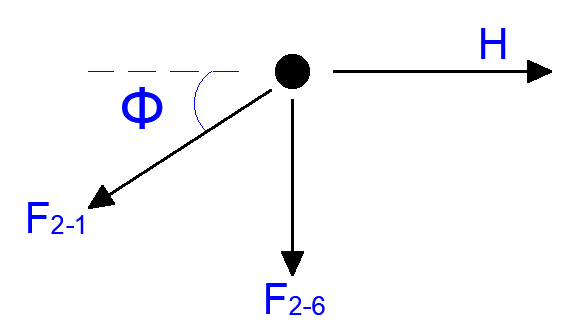
φ = tan^-1(1/6) = 9.46°

∑F_X = 0
-F_2-1cosφ + H = 0
-F_2-1cos9.46 – 45 = 0
-F_2-1 = 45/cos 9.46 = 45.62 kN
F_2-1 = -45.62 kN

∑F_Y = 0
-F_2-1sinφ – F_2-6 = 0
-F_2-6 = F_2-1sinφ
-F_2-6 = -45.62 sin9.46 = 7.498 kN
F_2-6 = 7.498 kN

Joint 1

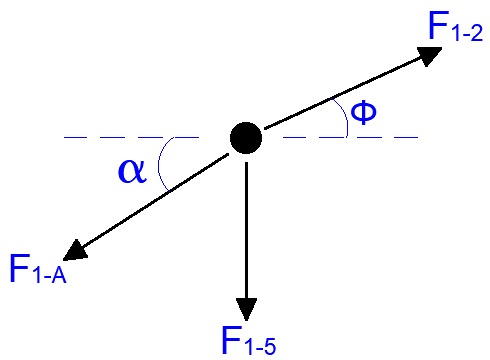
α = tan^-1(4/6) = 33.69°

∑F_X = 0
-F_1-Acosα + F_1-2sinφ = 0
-F_1-Acosα – 45.62sin(9.46) = 0
-F_1-A = 45.62sin(9.46)/cos(33.69) = 54.082 kN
F_1-A = -54.082 kN

∑F_y = 0
-F_1-Asinα + F_1-2sinφ – F_1-5 = 0
54.082sin(33.69) – 45.62sin9.46 – F_1-5 = 0
22.501 – F_1-5 = 0
F_1-5 = 22.501 kN

Therefore, the loading on the girder can be summarised as follows;

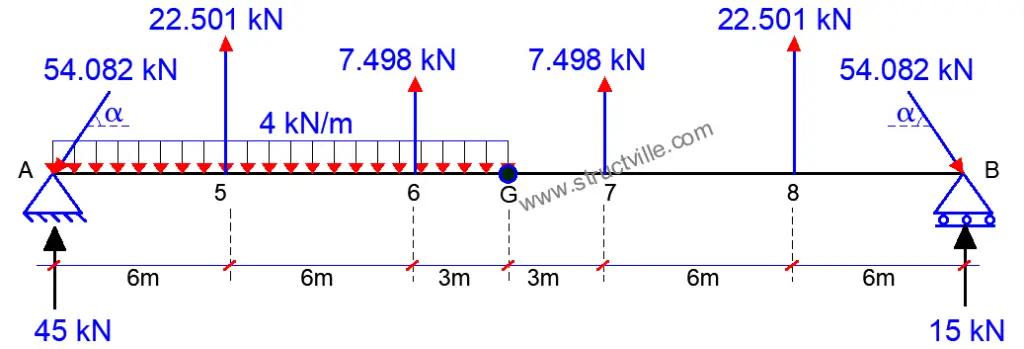
When the inclined forces are resolved into their vertical and horizontal components;

F_y = 54.082sinα = 54.082sin(33.69) = 30 kN
F_x = 54.082cosα = 54.082cos(33.69) = 45 kN

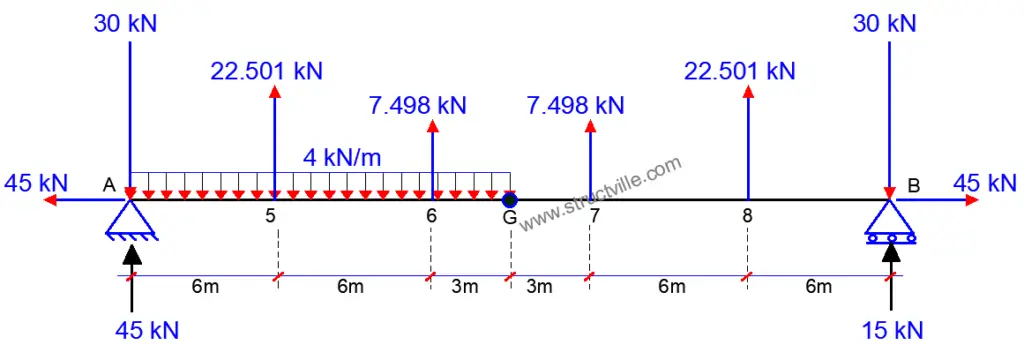
Check;
∑F_y ↑ = 45 + 15 + 2(22.501)+ 2(7.498) = 120 kN
∑F_y ↓ = (4 × 15) + 2(30) = 120 kN

Bending Moment

(Coming from the left)
M_A = 0
M₅ = (45 × 6) – (30 × 6) – (4 × 6²)/2 = 18 kNm
M₆ = (45 × 12) – (30 × 12) – (4 × 12²)/2 + (22.501 × 6) = 27 kNm
M_G^L = (45 × 15) – (30 × 15) – (4 × 15²)/2 + (22.501 × 9) + (7.498 × 3) = 0
(Coming from the right)
M_B = 0
M₈ = (15 × 6) – (30 × 6) = -90 kNm
M₇ = (15 × 12) – (30 × 12) + (22.501 × 6) = -45 kNm
M_G^R = (15 × 15) – (30 × 15) + (22.501 × 9) + (7.498 × 3) = 0

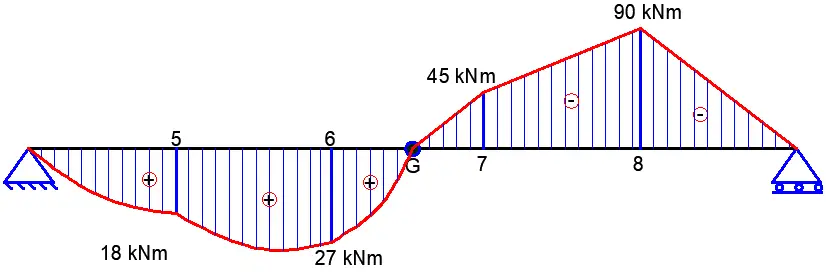
Shear Force

V_A = 45 – 30 = 15 kN
V₅^L = 45 – 30 – (4 × 6) = -9 kN
V₅^R = 45 – 30 – (4 × 6) + 22.501 = 13.501 kN
V₆^L = 45 – 30 – (4 × 12) + 22.501 = -10.499 kN
V₆^R = 45 – 30 – (4 × 12) + 22.501 + 7.498 = -3 kN
V_G = 45 – 30 – (4 × 15) + 22.501 + 7.498 = -15 kN
V₇^L = -15 kN
V₇^R = -15 + 7.498 = -7.502 kN
V₈^L = -7.502 kN
V₈^R = -7.502 + 22.510 = 15 kN
V_B = 15 kN

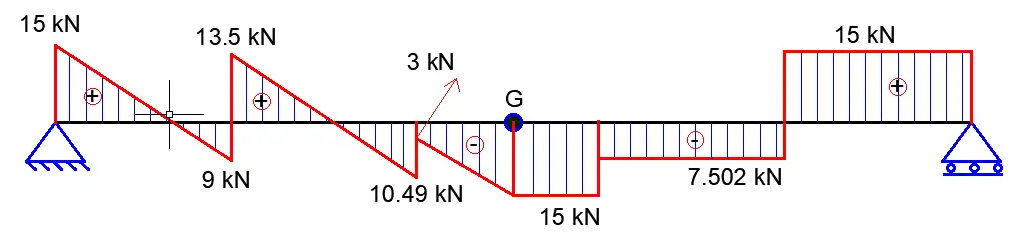
Axial Force

N_A-B = H = A_x = 45 kN (Tension)