Masonry is defined as an assemblage of masonry units (blocks, bricks, etc) laid in a specified pattern and joined together with mortar. They are usually used in components subjected to compressive loads such as walls, columns, arches, domes, vaults, etc. On other hand, masonry elements have limited capacity to support horizontal loads and bending moments.
Within the last decades, the efficiency of masonry units has increased due to higher allowable stresses, and refined possibilities in design. This, therefore, calls for more precision in the analysis, construction, and production of masonry to be used as structural members. This brings the design of masonry walls as a task of civil engineers.
Previous researches have shown that the out-of-plane (OOP) two-way bending failure of structural components can be one of the most predominant failure mechanisms in unreinforced masonry (URM) buildings. This is according to a submission from research carried out at the Faculty of Civil Engineering and Geosciences, Delft University of Technology, Netherlands. The study was published in the Elsevier – Structures journal in December 2020.
According to the researchers, extensive analytical formulations have been well developed for one-way vertically spanning walls, while analytical formulations for URM walls in OOP two-way bending require further improvement in accuracy and extension for the application range.
In order to bridge this knowledge gap, the researchers carried out an international testing campaign on a dataset of 46 testing specimens, in order to evaluate current analytical formulations. The current analytical formulations (codes of practice) used for the evaluation of the test specimens are;
- EN 1996-1-1:2005-Eurocode 6 (based on the yield line method),
- Australian Standard AS3700:2018 (based on the virtual work method), and
- two other virtual work formulations related to AS3700 (W2006 and G2019)
The analytical formulations that have been developed in the past decades were incorporated into design standards to assess the wall capacity in engineering practice. The current analytical formulations are mainly based on the yield line method or on the virtual work method.
The underlying assumptions used in the development of the yield line method are:
- masonry is simplified as a homogeneous material;
- all cracks develop simultaneously;
- the force capacity is calculated from the equilibrium between the applied forces and the reaction forces along cracking lines.
One drawback of the yield line method is that some crucial factors such as bonding patterns are neglected since masonry is considered as a homogenous material. This can affect the crack pattern therefore possibly resulting in misevaluation. Another drawback of the yield line method is that all cracks are assumed to develop concurrently, which can lead to inaccuracy for calculating the force capacity since contributions of all cracks are taken into account.
Read Also…
Unit weight of construction materials
How to calculate the quantity of mortar for laying blocks
Another category of analytical formulations originates from the virtual work method. The major underlying assumptions of the virtual work method are:
- the contributions from horizontal cracks are neglected;
- diagonal cracks start right from the wall corners;
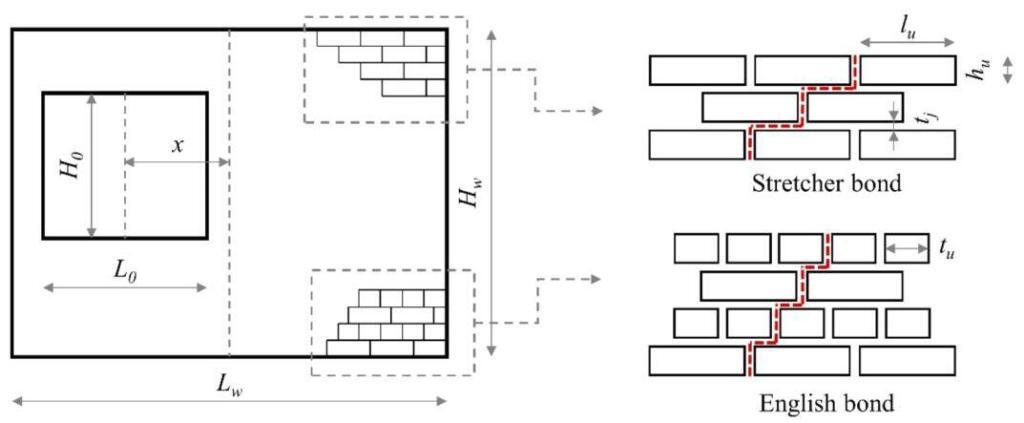
- the cracking pattern is assumed to follow the mortar joints and is determined by the aspect ratios of the units and of the wall; horizontal and diagonal bending moment capacities are calculated independently;
- the virtual work done by external loads is equal to the strain energy along cracking lines in pre-assumed cracking patterns
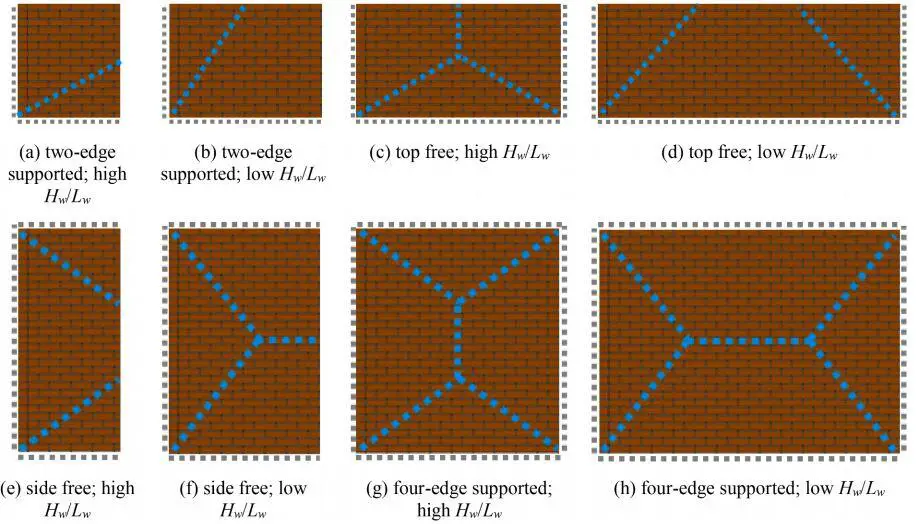
Additionally, the virtual work method provides coefficients and formulas to consider the presence of openings, while the yield line method does not. It is important to note that the afore-mentioned formulations are all force-based methods.
The dataset of the study carried out consists of tests performed mostly on clay brick and calcium silicate (CS) brick masonry walls. 37 out of 46 testing specimens were subjected to quasi-static cyclic loading, while the others to dynamic loading.
Eurocode 6 evaluates the force capacity w of a wall by following equation;
w = [(fx1 + σd)Z]/μα2Lw2 —— (1)
where the flexural strength ratio μ is defined as:
μ = (fx1 + σd)/fx2 —— (2)
Where;
fx1 and fx2 are the flexural strength of masonry obtained for planes of failure parallel to and perpendicular to the bed joints,
respectively;
σd is the vertical compressive stress at a specific height of the wall caused by self-weight and pre-compression σ;
Z is the section modulus of the wall;
α2 is the bending moment coefficient
The formulations AS3700, W2006 and G2019 assess the force capacity w of a wall by the following equation:
w = [2αf /Ld2] (k1Mh + k2Md) —— (3)
with the components of Eq. (3):
G = 2(hu + tj)/(lu + tj) —— (4)
α = GLd/Hd ——(5)
where;
Hd and Ld are the design height and design length of the wall, respectively
G is the assumed slope of the crack line;
α is the slope factor that identifies the expected cracking pattern including a vertical central crack in the case α < 1, or a horizontal central crack in the case α ≥ 1;
αf, k1 and k2 are coefficients determined by the presence of the openings, the slope factor α and the number of supported vertical edges
Mh and Md are the horizontal and the diagonal bending moment capacity of masonry, respectively.
The equations for Md and Mh are provided in the research article accordingly.
To compare the accuracy of the formulations, the tested force capacity from the dataset was predicted according to the equations of the analytical formulations. Lower and upper bounds for each testing specimen were calculated. The lower bound of the force capacity was estimated by considering the wall hinged on all sides in EC6 or assuming Rf = 0 in the other formulations; the upper bound of the force capacity was estimated by considering the wall clamped on all sides in EC6 or assuming Rf = 1 for the other formulations.
The comparison showed that EC6 has an incorrect prediction rate of 58.7% with the highest overestimation rate of 47.8%. W2006 and G2019 have incorrect prediction rates of 71.7% and 65.2%, respectively. Both these two formulations tend to underestimate the force capacity. AS3700 provides the lowest incorrect prediction rate of 56.6%. Also, the incorrect prediction rate on walls without openings of AS3700 is the lowest.
Table 1: Percentage of incorrect predictions for the considered dataset [1]
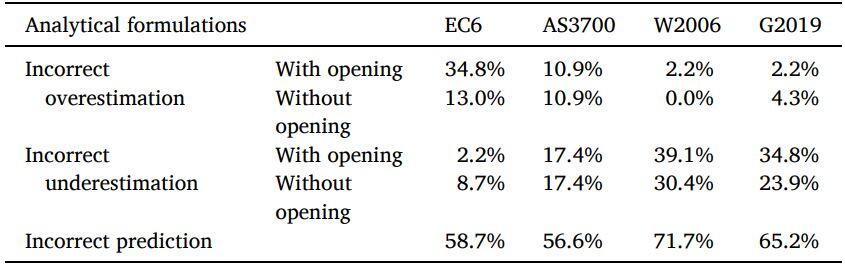
Nevertheless, the accuracy of AS3700 requires further improvement considering 21.8% and 34.8% of testing specimens are overestimated and underestimated, respectively. The formulations based on the virtual work method provide close incorrect prediction rates for walls with and without openings.
In conclusion, the formulations based on the virtual work method returned the most accurate predictions for the testing specimens evaluated in the study, especially for partially clamped walls and walls with openings. Nevertheless, drawbacks and limitations were revealed when analytical formulations were applied to assess the influence of crucial factors on the force capacity such as precompression of the wall, bonding pattern, boundary conditions, material properties, area of openings, and eccentricity of load.
To improve the accuracy and application range of the analytical formulations, further study is suggested regarding the influence of above-mentioned crucial factors on the wall failure mechanisms and quantifying the relations between the force capacity and the crucial factors.
Disclaimer
The contents of this article are culled from [Lang-Zi Chang, Francesco Messali, Rita Esposito (2020): Capacity of unreinforced masonry walls in out-of-plane two-way bending: A review of analytical formulations. Structures 28 (2020) 2341-2477] and does not belong to www.structville.com. It has been presented here in accordance to the requirements of open access articles under the CC BY license (http://creativecommons.org/licenses/by/4.0/)
References
[1] Lang-Zi Chang, Francesco Messali, Rita Esposito (2020): Capacity of unreinforced masonry walls in out-of-plane two-way bending: A review of analytical formulations. Structures 28 (2020) 2341-2477 https://doi.org/10.1016/j.istruc.2020.10.060