Fire Resistance Design of Steel Beams

In the event of a fire, the general objectives of fire protection of structures are to limit hazards to individuals and society, adjacent property, and, where necessary, the environment or immediately exposed property (EN 1993-1-2:2005). The relevant time of fire exposure during which the associated fire resistance function of a structure is maintained despite fire actions is characterized as fire resistance in terms of time. Therefore, the fire resistance design of steel beams is concerned with maintaining the load-bearing function, integrity separating function, and thermal insulating separating function of a steel beam for a given period of time.

According to the Construction Products Directive 8911 06/EEC, the following are the essential requirement for the limitation of fire risks:

“The construction works must be designed and built in such a way, that in the event of an outbreak of fire;

• the load bearing resistance of the construction can be assumed for a specified period of time
• the generation and spread of fire and smoke within the works are limited
• the spread of fire to neighbouring construction works is limited
• the occupants can leave the works or can be rescued by other means
• the safety of rescue teams is taken into consideration”.

According to the European standards, three major criteria are used to define the fire resistance of structures:

R – load-bearing function
E – integrity separating function
I – thermal insulating separation function

It is important to note that the above criteria may be required individually or in combination:
• separating only: integrity (criterion E) and, when requested, insulation (criterion I)
• load bearing only: mechanical resistance (criterion R)
• separating and load-bearing: criteria R, E and, when requested I

Where mechanical resistance in the case of fire is required, steel structures shall be designed and constructed in such a way that they maintain their load-bearing function the relevant fire exposure. Criterion “R” is assumed to be satisfied in steel beams where the load-bearing function is maintained during the required time of fire exposure.

For a given load level, the temperature at which failure is expected to occur in a structural steel element for a uniform temperature distribution is called the critical temperature (θ_crit). The thermal action on the steel member is a result of the heat flux transferred from the fire to the steel member. This is usually regarded as an indirect action.

The load bearing function of a structure is satisfied only if during the relevant duration of fire exposure t;

E_fi,d,t ≤ R_fi,d,t

where
E_fi,d,t: design effect of actions (Eurocodes 0 and 1)
R_fi,d,t: corresponding design resistance of the structure at instant t

It is however important to note that Eurocode permits the fire resistance of steel structures to be assessed in any of these three domains;

Time; t_fi,d ≤ t_fi,req (this usually feasible using advanced computational models)
Load Resistance; E_fi,d,t ≤ R_fi,d,t (This approach is feasible by hand calculation. Find reduced resistance at required resistance time)
Temperature; θ_cr,d ≤ θ_d (The most simple approach, find the critical temperature for loading, compare with design temperature)

For ordinary structural fire structural design of steel beams, simple calculation models such as critical temperature can be used.

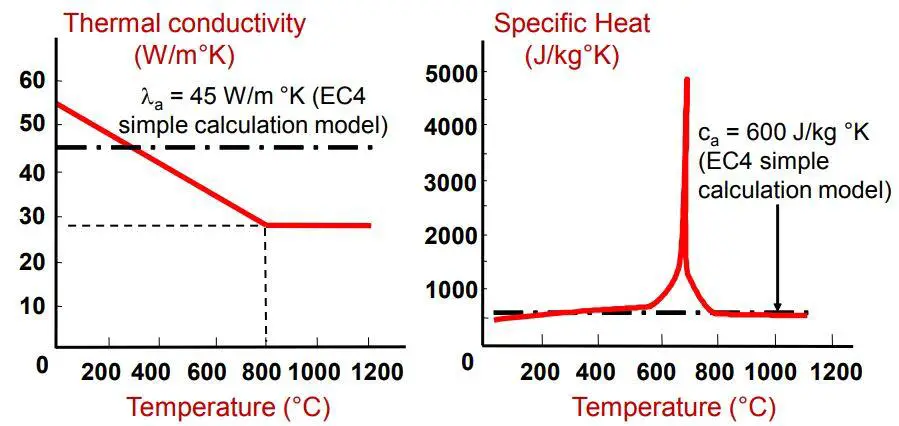
The thermal properties of structural steel at elevated temperature is shown below. At about 600°C, the elastic modulus of elasticity of steel is reduced by about 70% while the yield strength reduces by about 50%.

Under fire situation, the design loading is given by;

E_fi,d,t = ∑G_k,j + ψ_2,1Q_k,1 + ∑ψ_2,1Q_k,I

More commonly, a reduction factor η_fi is applied to the loading under ambient conditions in order to represent the loading under fire conditions. This is given by;

E_fi,d,t = η_fiE_d

η_fi = E_fi,d,t/R_d

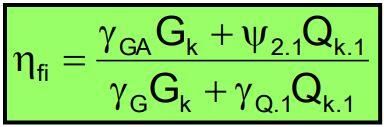
In ambient temperature strength design;
γ_G = 1.35 (Permanent loads)
γ_Q.1 = 1.50 (Combination factor; variable loads)

In structural fire design
γ_GA = 1.0 (Permanent loads; accidental design situations)
γ_2.1 = 0.3 (Combination factor; variable loads, offices)

Steps in the Fire Resitance Design of Steel Beams

The following are the steps to follow when assessing the fire resistance design of steel beams;

(1) Evaluate the actions on the structuture in fire situation E_fi.d. This is commonly achieved by applying a reduction factor to the ambient temperature load.
(2) Classify the member under class 1, class 2, class 3 or class 4 depending the rotation capacity using EC3 guidelines
(3) Evaluate the resistance of the structure at ambient temperature (20°C) by fire rules R_fi.d.20.
(4) Calculate the degree of utilisation μ₀
(5) Calculate the critical temperature θ_cr
(6) Calculate the section factor A_m/V and the correction factor k_sh
(7) Carry out step by step calculation to verify if θ_fi,d = θ_cr at the time of fire exposure t_fi,d
(8) Check if t_fi,d is greater than the required fire resistance period of the structure t_req

Design Example of Fire Resistance of Steel Beams

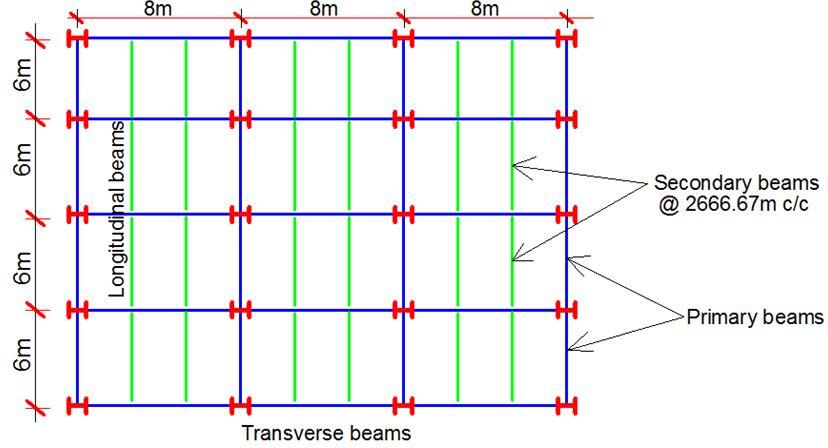
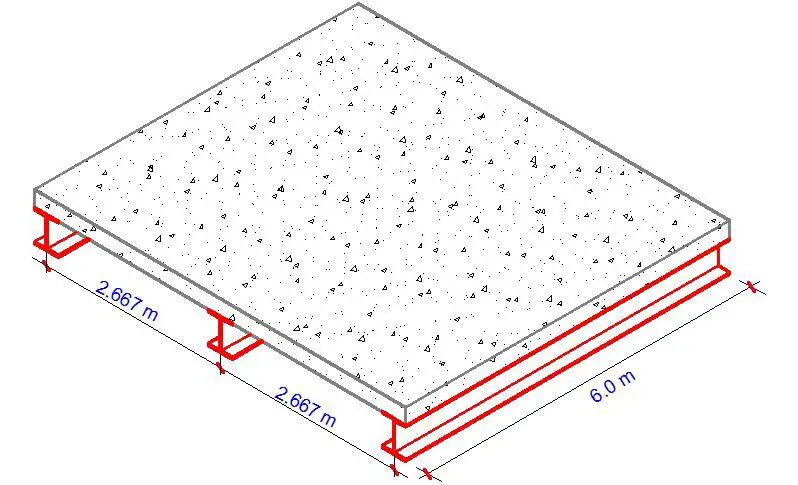
Verify the fire resistance of an intermediate secondary beam (S275) in an office block supporting a slab of 175 mm thickness. The expected fire rating is 30 minutes. The slab is to support a variable action of 3 kN/m², and finishes of 1.5 kN/m².

Design Data

Imposed variable load q_k = 3.0 kN/m²
Thickness of R.C. slab = 150 mm
Finishes = 1.5 kN/m²

Analysis and Design at Normal Room Temperature
Permanent loads

Unit weight of reinforced concrete = 25 kN/m³
Thickness of slab = 150 mm = 0.15 m

Self weight of slab = 25 × 0.15 = 3.75 kN/m²
Weight of finishes = 1.5 kN/m²
Total permanent actions (g_k) = 5.25 kN/m²

Variable Actions
Imposed variable load = 3.0 kN/m²
Total live load (q_k) = 3.0 kN/m²

Normal Temperature Design of the Secondary Beam

The load transferred from the slab to the secondary beams considering a bay width of 2.667m

At ultimate limit state (neglecting reduction factors);
P_Ed = 1.35g_k + 1.5g_k
P_Ed = 1.35(5.25) + 1.5(3) = 11.6 kN/m²

Ultimate load transferred to every secondary beam;
F_d = 11.6 kN/m² × 2.667m = 30.937 kN/m
Self weight of beam = 1.35 × 0.392 = 0.528 kN/m
Total design load on the beam = 30.937 + 0.528 = 31.465 kN/m

M_y,Ed = (F_d.L²)/8 = (31.465 × 6²)/8 = 141.592 kNm
V_Ed = (F_d.L)/2 = (31.465 × 6)/2 = 94.395 kN

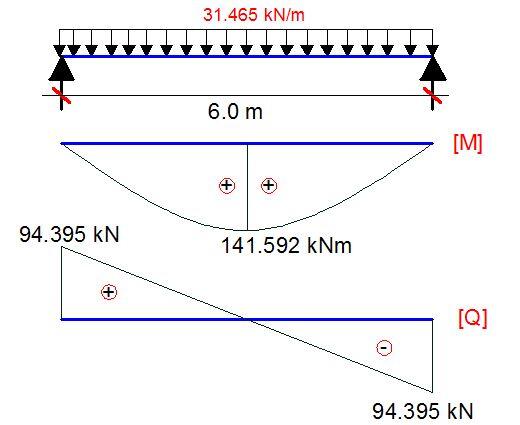
An advanced UK beam S275 is to be used for this design.
f_y = 275 N/mm²
γ_m0 = 1.0 (Clause 6.1(1) NA 2.15 BS EN 1993-1- 1:2005)

The required section is supposed to have a plastic modulus about the y-y axis that is greater than;
W_pl,y = M_y,Ed.γ_m0/f_y
W_pl,y = (150.093 × 10³ × 1.0)/275 = 545.792 cm³

From steel tables, try section UB 305 x 165 x 40        W_pl,y = 623 cm³

Properties
h = 303.4 mm; b = 165 mm; d = 265.2 mm; t_w = 6.0 mm; t_f = 10.2 mm; r = 8.9 mm; A = 51.3 cm⁴; I_y = 8500 cm⁴; I_z = 764 cm⁴; W_el,y = 560 cm³;

h_w = h – 2t_f = 265.2 mm
E (Modulus of elasticity) = 210000 N/mm²  (Clause 3.2.6(1))

Classification of section
ε = √(235/f_y) = √(235/275) = 0.92 (Table 5.2 BS EN 1993-1- 1:2005)

Outstand flange: flange under uniform compression c = (b – t_w – 2r)/2 = [165 – 6 – 2(8.9)]/2 = 70.6 mm
c/t_f = 70.6/10.2 = 6.921

The limiting value for class 1 is c/t_f  ≤ 9ε = 9 × 0.92
5.03 < 8.28
Therefore, outstand flange in compression is class 1

Internal Compression Part (Web under pure bending)
c = d = 265.2 mm
c/t_w = 265.2/6 = 44.2
The limiting value for class 1 is c/t_w ≤ 72ε = 72 × 0.92 = 66.24
44.2 < 66.24
Therefore, the web is plastic. Therefore, the entire section is class 1 plastic.

Member Resistance Verification

Moment Resistance

For the structure under consideration, the maximum bending moment occurs where the shear force is zeo. Therefore, the bending moment does not need to be reduced for the presence of shear force (clause 6.2.8(2)).

M_Ed/M_c,Rd ≤  1.0 (clause 6.2.5(1))
M_c,Rd = M_pl,Rd = (M_pl,y × F_y)/γ_m0

M_c,Rd = M_pl,Rd = [(623 × 275)/1.0] × 10^-3 = 171.325 kNm

M_Ed = 141.592 kNm
M_Ed/M_c,Rd = 141.592/171.325 = 0.825 < 1.0 Ok

Shear Resistance (clause 6.6.2)

The basic design requirement is;
V_Ed/V_c,Rd ≤  1.0

V_c,Rd = V_pl,Rd = A_v(F_y / √3)/γ_m0 (for class 1 sections)

For rolled I-section with shear parallel to the web, the shear area is;
A_v = A – 2bt_f + (t_w + 2r)t_f (for class 1 sections) but not less than ηh_wt_w
A_v = (51.3 × 10² – (2 × 165 × 10.2) + [6 + 2(8.9)] × 10.2 = 2006.76 mm²
η = 1.0 (conservative)
ηh_wt_w = (1.0 × 265.2 × 6) = 1591.2 mm²
2006.76 > 1591.2
Therefore, A_v = 2006.76 mm²

The shear resistance is therefore;
V_c,Rd = V_pl,Rd = [2006.76 × (275/ √3)/1.0]  × 10^-3 = 318.6159 kN
V_Ed/V_c,Rd = 94.395/318.62 = 0.296 < 1.0 Ok

Shear Buckling

Shear buckling of the unstiffnened web will not need to be considered if;
h_w/t_w ≤  72ε/η
h_w/t_w = 265.2/6 = 44.2
72ε/η  = (72 ×  0.92)/1.0  = 66
44.2 < 66 Therefore shear buckling need not be considered.

Serviceability limit state

Vertical deflections are computed based on unfactored variable loads. Permanent loads need not be considered (BS EN 1993-1-1 NA 2.23)

q_k = 3.0 × 2.667 = 8 kN/m
w = 5ql⁴/384EI
w = (5 × 8 × 6000⁴)/(384 × 210000 × 8500 × 10⁴) = 7.563 mm 
Span/360 = 6000/360 = 16.667 (BS EN 1993-1-1 NA 2.23)

7.563 < 16.667
Therefore, deflection is satisfactory

Fire Design of the Secondary Beam

The loading due to fire design is given by;

E_fi,d,t = ∑G_k,j + ψ_2,1Q_k,1 + ∑ψ_2,1Q_k,I

As a simplification to the loading above, the fire part of EC 3 permits us to apply a reduction factor η_fi to the load of normal temperature design.

η_fi = (γ_GAG_k + ψ_2,1 Q_k,1)/(γ_GG_k + γ_QQ_k,1)

For the secondary beams;
G_k = 5.25 × 2.667 = 14.0 kN/m
Q_k = 3.0 × 2.667 = 8.0 kN/m

ψ_2,1 = 0.3
γ_G = 1.35
γ_GA = 1.0
γ_Q = 1.5

η_fi = [14 + (0.3 × 8)] / [(1.35 × 14) + (1.5 × 8)] = 0.53
Bending moment; M_fi,d,t = 0.53M_Ed = 0.53 × 141.592 = 75 kNm
Shear force; V_fi,d,t = 0.53V_Ed = 0.53 × 94.395 = 50 kN

According to equation 4.2 of EN 1993-1-2 for fire resistance design;
ε = 0.85√(235/f_y) = 0.786 for S275 grade of steel
Outstand flange: flange under uniform compression c = (b – tw – 2r)/2 = [165 – 6 – 2(8.9)]/2 = 70.6 mm

c/t_f = 70.6/10.2 = 6.921

The limiting value for class 1 is c/t_f ≤ 9ε = 9 × 0.786
(c/t_f)5.03 < (9ε) 7.074
Therefore, outstand flange in compression is class 1

Internal Compression Part (Web under pure bending)
c = d = 265.2 mm
c/t_w = 265.2/6 = 44.2

The limiting value for class 1 is c/tw ≤ 72ε = 72 × 0.786 = 56.592
44.2 < 56.592
Therefore, the web is plastic. Therefore, the entire section is class 1 plastic under fire loading.

From our calculations for normal temperature design, it can be verified that;
M_c,Rd = M_pl,Rd = 171.325 kNm
V_c,Rd = V_pl,Rd = = 318.6159 KN

From relation 4.24 of EN 1993-1-2;
We can calculate the utilisation ratio of the unprotected steel beam;

With respect to bending moment;
μ_0,m = η_fi (γ_m,0/γ_m,fi) = (M_fi,d,t/M_Rd) × (γ_m,0/γ_m,fi) = (75/171.325) × (1.0/1.0) = 0.437 < 1.0

With respect to vertical shear;
μ_0,v = η_fi (γ_m,0/γ_m,fi) = (V_fi,d,t/V_Rd) × (γ_m,0/γ_m,fi) = (50/318.6159) × (1.0/1.0) = 0.156 < 1.0

As the beam supports the concrete slab above, the impact of the kappa factors relative to the temperature gradient over its depth have to be taken into account. However, they have an impact on bending moment alone. No rule is provided for shear.

The modified degree of utilisation for bending moment;
κ₁ = 1.0
κ₂ = 1.0

For the unprotected beam having all four sides exposed – clause 4.1(16) of EN 1993-1-2

μ_0,m,k = μ_0,m(κ₁ κ₂) = 0.463 × (1.0 × 1.0) = 0.463

The modified degree of utilisation factor for vertical shear
μ_0,v,k = μ_0,v = 0.166
μ₀ = max (μ_0,m,k; μ_0,v,k)
μ₀ = max (0.463; 0.166) = 0.463

Calculation of the critical temperature of the unprotected beam;

Using simplified equation from Equation 4.22 of EN 1993-1-2;

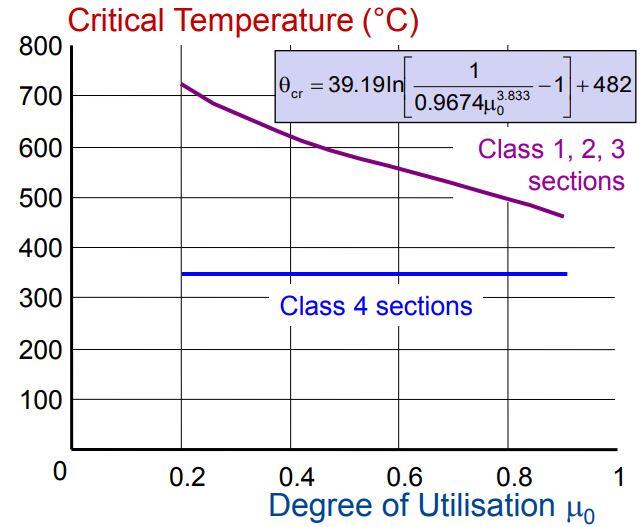
θ_cr = 39.19In[1/(0.9674μ₀^3.833) – 1] + 482
θ_cr = 39.19In[1/(0.9674 ×0.463^3.833) – 1] + 482 = 596°C

From a more accurate linear interpolation from reduction table (Table 3.1);
k_y,θ (0.47) = 600°C
k_y,θ (0.463) = ??
k_y,θ (0.23) = 700°C

θ_cr = 600 + (0.463 – 0.47 )/(0.23 – 0.47) × (700 – 600) ≈ 603°C

For the protected section due to protection of the three sides exposed to fire;
κ₁ = 0.85 (three sides exposed; insulated)
κ₂ = 1.0 (for the unprotected beam having all four sides exposed – clause 4.1(16) of EN 1993-1-2

μ_0,m,k = μ_0,m(κ₁ κ₂) = 0.463 × (0.85 × 1.0) = 0.393

The modified degree of utilisation factor for vertical shear
μ_0,v,k = μ_0,v = 0.166 (no adaptation factor)
μ₀ = max (μ_0,m,k; μ_0,v,k)
μ₀ = max (0.393; 0.166) = 0.393

Critical temperature of the protected beam
From equation 4.22 of EN 1993-1-2;
θ_cr = 39.19In[1/(0.9674μ₀^3.833)- 1] + 482
θ_cr = 39.19In[1/(0.9674 × 0.393^3.833 )- 1] + 482 = 622°C

From a more accurate linear interpolation from reduction table (Table 3.1);
k_y,θ (0.47) = 600°C
k_y,θ (0.393) = ??
k_y,θ (0.23) = 700°C

θ_cr = 600 + (0.393 – 0.47 )/(0.23 – 0.47) × (700 – 600) ≈ 632°C

Section factor of the unprotected steel beam

Section factor is the ratio of the perimeter of the beam exposed to fire to the volume of the beam section (A_m/V). In other words, it is the ratio between “perimeter through which heat is transferred to steel” and “steel volume”.

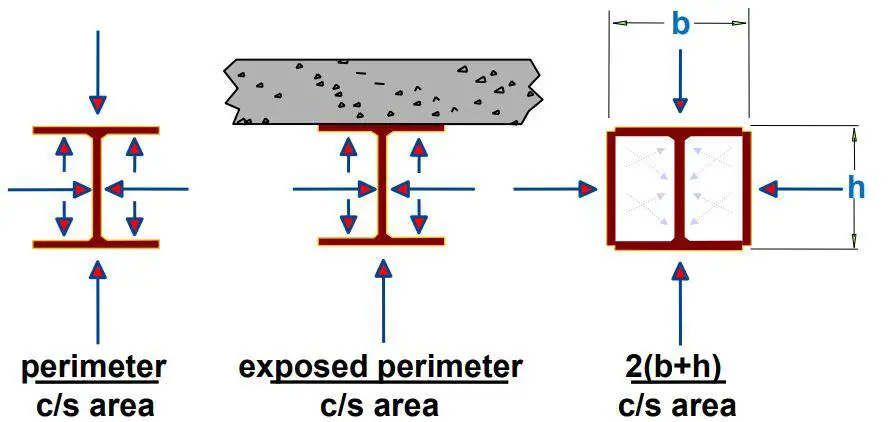
From steel table;
A_m/V = 240 m^-1 (for UKB 305 x 165 x 40)
(A_m/V)_b = 185 m^-1 (boxed value)

The correction factor for shadow effect;
k_sh = 0.9(A_m/V)_b / (A_m/V)
k_sh = (0.9 × 185)/240 = 0.6937

Heating of the unprotected beam
The heating of the beam can be obtained from relation 4.25 of EN 1993-1-2.

Δθ_a.t = (k_sh/(c_a ρ_a) × A_m/V × h_net,d × Δt —– (1)

We will apply this relationship with the following assumptions;
Δt = time interval increments = 5 seconds
ρ_a = density of steel = 7850 kg/m³
c_a = specific heat of steel = 600 J/kgK
θ_a.t = 0.6937/(600 × 7850) × 240 × h_net,d × 5

Therefore;
θ_a.t = (1.7664 × 10^-4)h_net,d

h_net,d (heat flux) has two parts (the convective part h_net,c and the radiative part h_net,r) and varies with time as shown in the equation below. It can be easily calculated if the gas temperature θ_g is known.

h_net,d = h_net,r + h_net,c

h_net,r = (5.67 × 10^-8)ϕε_res [(θ_g + 273)⁴ – (θ_m + 273)⁴]
h_net,c = α_c (θ_g – θ_m)

Under standard fire situations;
ε_res = ε_f × ε_m = 0.7 (ε_f is the emissivity of the fire usually taken as 1.0 while ε_m is the surface emissivity of the member usually taken as 0.7 for carbon steel)
ϕ (view factor or configuration factor) = 1.0
α_c = the coefficient of heat transfer by convection = 25 W/m²K

Therefore;
h_net,r = 3.969 × 10^-8[(θ_g + 273)⁴ – (θ_m + 273)⁴]
h_net,c = 25(θ_g – θ_m)
θ_g = 20 + 345log(8t + 1) (t in minutes)
θ_m is the surface temperature of the steel member

The most relevant way to deal with h_net,d is to consider a mean value within the time interval ∆t (5 seconds in this case) between the instant t_i and t_i+1

h_net,r = 3.969 × 10^-8{[(θ_g,i + 273)⁴ + (θ_g,i+1 + 273)⁴)]/2- (θ_a,i + 273)⁴}
h_net,c = 25[(θ_g,i + θ_g,i+1)/2 – θ_a,i]

When this is solved iteratively, the time at which the bare section reaches critical temperature can be obtained. The temperature development curve can also be plotted. By programming Eq. (1), it is easy to build tables or nomograms like the ones presented in Annex A of Franssen and Real (2015) for unprotected steel profiles subjected to the ISO 834 fire curve. The use of these tables and nomograms avoids the need to solve Eq. (1). The nomograms from Annex A are reproduced in the Figure below.

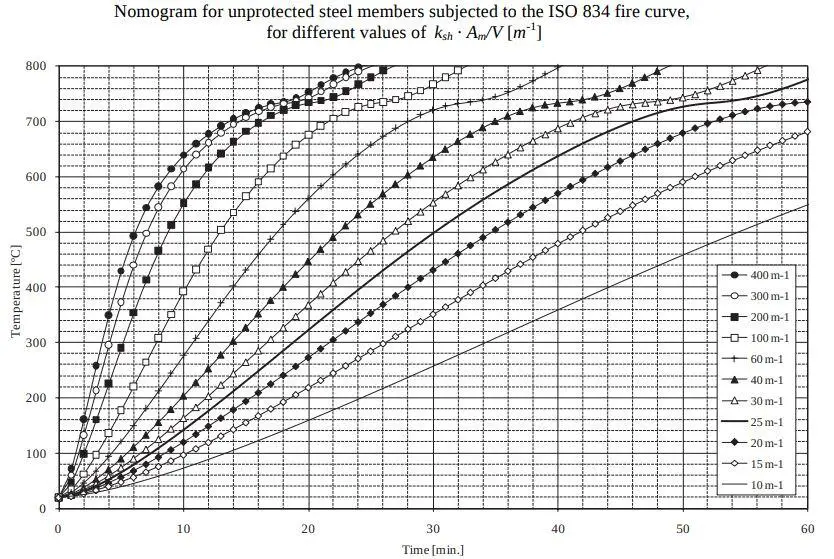
k_shA_m/V = 166.5 m^-1

For a critical temperature of 603°C (for the unprotected beam) and k_shA_m/V of 166.5 m^-1, the time to achieve that temperature when exposed to fire is about 14 minutes. This is less than 30 minutes, therefore the beam cannot be designated as R30.

In the temperature domain;
Table 4.6 gives the temperature after 30 minutes and 60 minutes of standard fire ISO 834 exposure, for different values of the modified section factor k_sh[A_m/V].

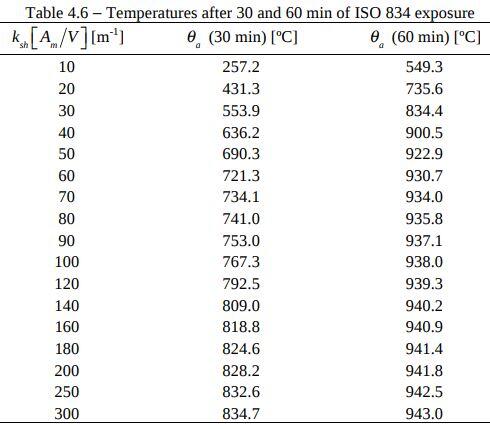
From Table 4.6, the critical temperature for 30 mins for k_sh[A_m/V] = 166.5 m^-1 fire is 825.185°C. Therefore, the temperature in the section exposed on 4 sides after 30 min of standard fire ISO 834 exposure is 825.185°C. As this temperature is greater than the critical temperature, the member doesn’t fulfil the condition for temperature approach verification, because:

θ_d > θ_cr,d , at time t_fi,requ

This further confirms that the member does not satisfy R30 requirements.