Analysis and Design of V-Shaped Beams

Beams that have V-shapes (in the plan view) are commonly found in the corners of residential and commercial buildings. According to Hassoun and Al-Manaseer (2008), such beams can be analysed and designed using strain-energy principles especially when the beam is fixed at both ends.

In some scenarios, engineers may be tempted to design v-shaped beams as two cantilevers meeting at a point, but this is not strictly the case. There will be a need to assess other internal stresses such as torsion, and to understand the actual nature of the distribution of internal forces.

For a v-shaped beam subjected to a uniformly distributed load w (kN/m), the internal forces in the members can be obtained as follows;

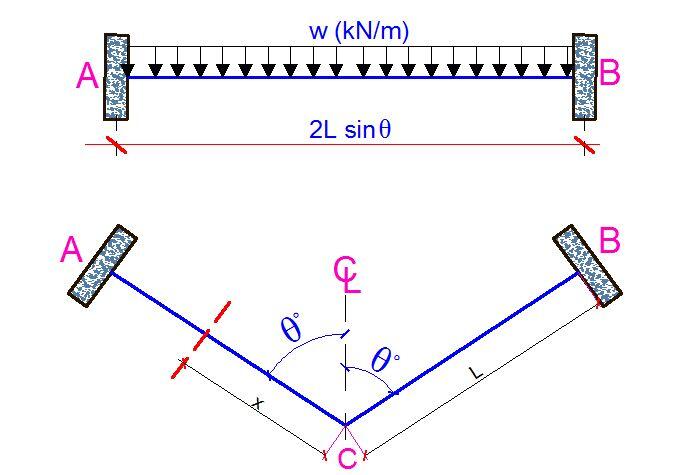
(The bending moment at the centre of the beam M_c is given by;
M_c = (wL²)/6 × [sin²θ/(sin²θ + λcos²θ)

Where;
λ = EI/GJ
L = half the total length of the beam AC
θ = Half the angle between the two sides of the v-shape beam.

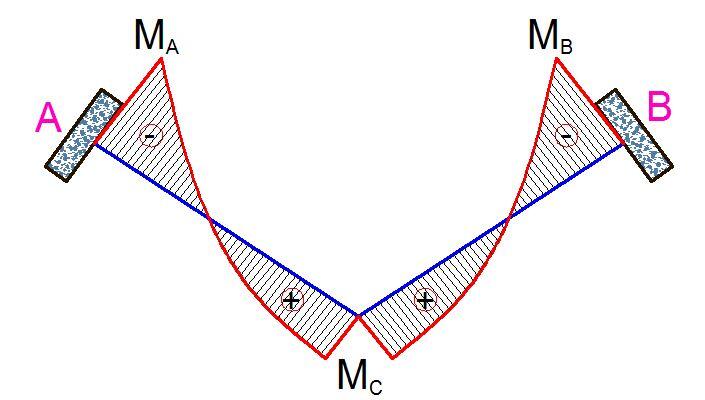
The torsional moment at the centreline of the section is given by;
T_C = (M_C/sinθ) × cosθ = M_CCotθ

At any section N along the length of the beam at a distance x from the centreline C,

M_N = M_C – wx²/2
T_N = T_C = M_CCotθ (constant torsional moment)

At the supports, let x = L
M_A = M_C – wL²/2

Worked Example

A v-shaped beam at the corner of a building has a depth of 400mm and a width of 225 mm. The plan view of the beam is shown below. It is to support an ultimate uniformly distributed load of 30 kN/m inclusive of the factored self-weight. Design the beam according to the requirements of EC2. f_ck = 30 MPa, f_yk = 500 MPa, Concrete cover = 35 mm

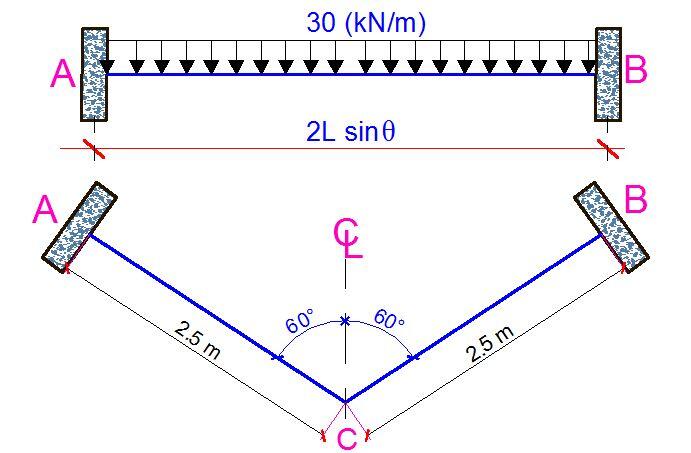
Solution

For f_ck = 30 MPa,
Modulus of elasticity E_cm = 31476 MPa
Shear modulus G = E_cm/2(1 + v) = 31476/2(1 + 0.2) = 13115 MPa
Moment of inertia I = bd³/12 = (225 × 400³)/12 = 12 × 10⁸ mm⁴
Polar moment of inertia J = 985033091.649413 mm⁴
λ = EI/GJ = (31476 × 12 × 10⁸)/(13115 × 985033091.649413) = 2.9237

M_c = [wl²sin²θ/6(sin²θ + λcos²θ) = (30 × 2.5² × 0.75)/[6 × (0.75 + 2.9237 × 0.25)] = 140.625/8.88555 = 15.755 kNm
M_A = M_B = M_C – wl²/2 = 15.755 – (30 x 2.5²)/2 = -77.995 kNm
Torsional moment = T_A = M_Ccotθ = 15.755 x 0.5773 = 9.095 kNm
Shear at support = V_A = V_B = 30 × 2.5 = 75 kN

Let us check these answers using Staad Pro software;

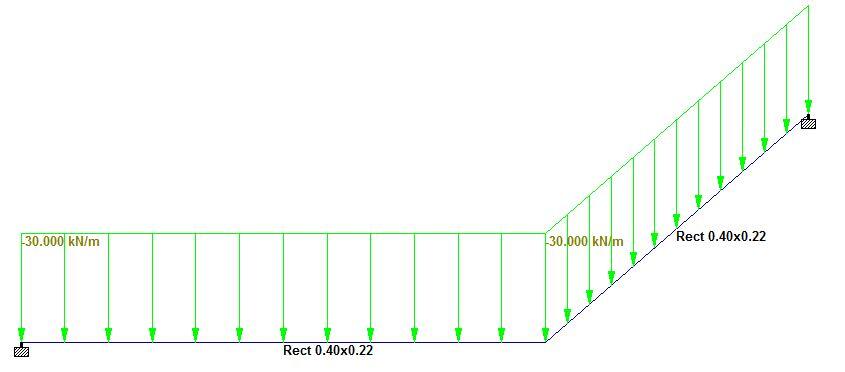
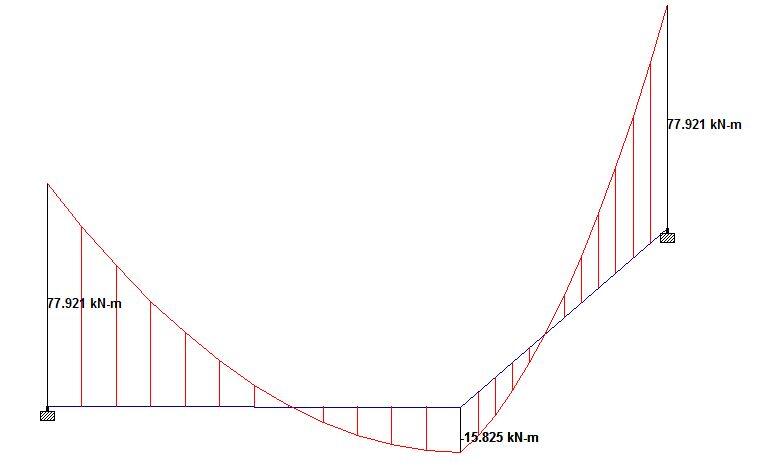
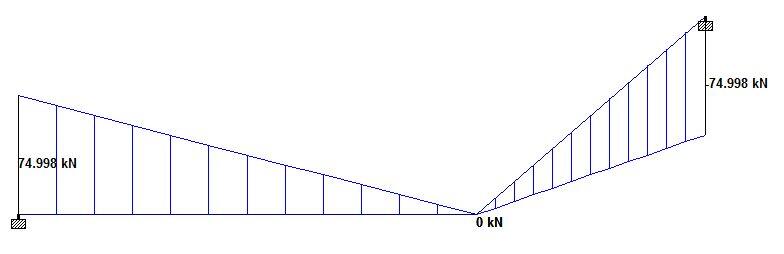
By implication, one can confirm that the analysis method adopted is accurate. The beam can now be designed for torsion, bending, and shear using the guidelines provided in EN 1992-1-1:2004.

References
Hassoun N. M. and Al-Manaseer A. (2008): Structural Concrete Theory and Design. Wiley and Sons Inc, New Jersey, USA