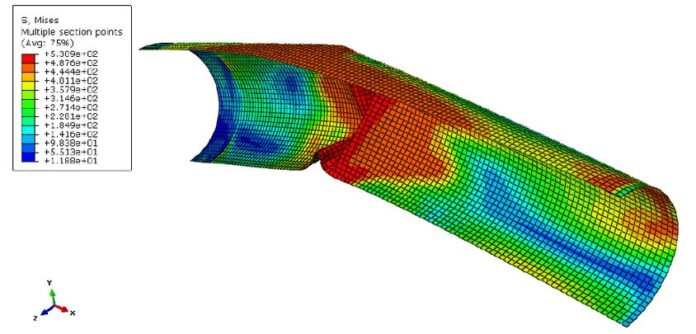
In structural engineering, understanding stress and its impact on the materials to be used for construction is very important. One of the most widely used theories for assessing material failure is the Von-Mises stress criterion. In this brief article, we explore the physical significance of Von-Mises stress and its application in the design of steel structures.
Von Mises stress is a scalar value derived from the multi-axial stress state that provides a simplified metric for predicting yielding in ductile materials. The stress state within a material under load is not always a simple uniaxial tension or compression.
In most practical scenarios, a combination of normal and shear stresses act simultaneously, resulting in a multi-axial stress state. Analyzing and visualizing such complex stress states can be challenging. The von Mises yield criterion, proposed by Richard von Mises in 1913, offers a simplified approach to assess the potential for yielding in ductile materials under multi-axial loading.
Theoretical Foundation
The von Mises stress is based on the distortion energy theory, which postulates that yielding occurs when the distortion energy per unit volume reaches a critical value. Distortion energy refers to the energy stored in the material due to its deformation (excluding the volumetric change associated with hydrostatic pressure). Mathematically, the von Mises stress (σvm) is defined as:
σVM = √(σ₁² + σ₂² + σ₃² – σ₁σ₂ – σ₂σ₃ – σ₃σ₁)
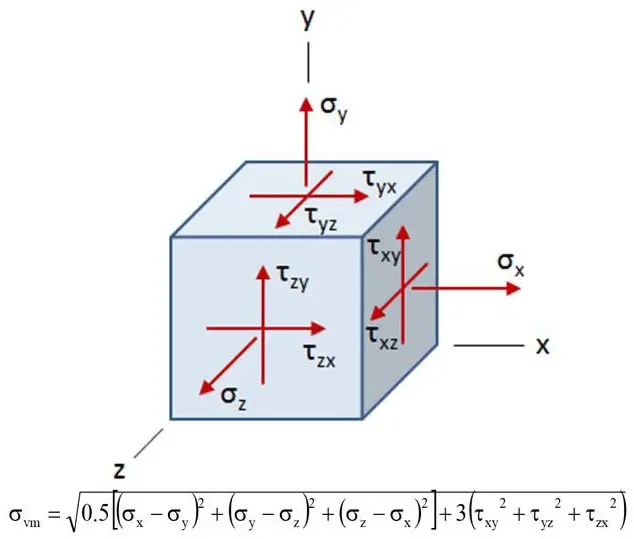
Application of von Mises Stress in the Design of Steel Structures
Steel structures experience complex, multi-axial stress states – a far cry from the uniaxial tension or compression encountered in textbooks. Analyzing and visualizing these variable stress states can be cumbersome. The genius of von Mises stress lies in its ability to simplify this complexity into a single scalar value. By focusing on distortion energy, a measure of deformation excluding volumetric changes, it essentially condenses the multi-axial stress state into a single, meaningful indicator of potential yielding.
For ductile materials like steel, exceeding the yield strength signifies the onset of plastic deformation. By comparing the calculated von Mises stress at critical points in the structure with the steel’s yield strength, engineers gain invaluable insights:
The von Mises stress plays a very important role in various engineering design and analysis scenarios:
- Finite Element Analysis (FEA): In FEA software, complex structures are discretized into small elements, and stress tensors are calculated at each element point. The von Mises stress is often used as a failure criterion by comparing it to the material’s yield strength. If the von Mises stress exceeds the yield strength at any point, it indicates potential plastic deformation or yielding.
- Pressure Vessel Design: Pressure vessels experience complex stress states due to internal pressure and external loads. Analyzing the von Mises stress distribution helps ensure the vessel remains within its safe operating limits and prevents catastrophic failure.
- Bridges and Buildings: From towering bridges to intricate beam-column connections, engineers rely on von Mises stress to assess the load-carrying capacity of steel members, optimizing their design to withstand diverse loading conditions like wind, seismic forces, and live loads.
EN 1993-1-5 (Part 1-5 of Eurocode 3) entitled “Plated Structural Elements”, establishes the regulations for preventing local buckling in steel plated structures. This section presents designers with two primary design methodologies: the “Effective Width Method” and the “Reduced Stress Method“.
The Reduced Stress Method offers a simplified approach compared to the general form, making it particularly suitable for serviceability checks and designing non-uniform members such as tapered beams, webs with openings, and plates with non-orthogonal stiffeners. This method assumes a linear stress distribution up to the buckling limit of the first-yielding plate element. The entire cross-section remains fully effective until this stress limit is reached.
The Reduced Stress Method can be employed to determine stress limits for both stiffened and unstiffened plates. It incorporates the von Mises criterion to account for the interaction between various stress types within the plate.
Furthermore, Eurocode 3 Part 6, permits the use of ”stress design” approach for the limit state design of steel shells. When employing the stress design approach, limit states must be evaluated across three distinct stress categories: primary, secondary, and local. This categorization typically relies on the von Mises equivalent stress at specific points. However, it is very important to recognize that this value is not suitable for assessing buckling stresses.
Factor of Safety
If we define the safety factor as N = Failure Stress / Analysed Stress
For Von-Mises Stresses, the safety factor is computed using;
N = fy / σvm = Yield stress/von Mises stress
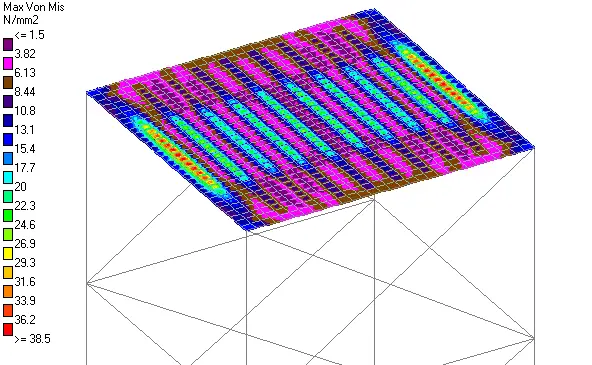
For instance, if the steel plate above is to be constructed with steel grade S275 (fy = 275 N/mm2), the factor of safety using von Mises criteria is;
Factor of Safety = (0.65 × 275)/38.5 = 4.64
In this case, the failure stress is taken as 0.65fy.
Limitations and Considerations
It is important to remember that the von Mises stress is a simplified criterion and has certain limitations:
- Material Dependence: The von Mises criterion is primarily applicable to ductile metals. It may not be accurate for brittle materials or materials with significant pressure sensitivity.
- Anisotropy: The criterion assumes isotropic material behaviour, meaning the material properties are the same in all directions. If a material exhibits anisotropic behaviour, alternative yield criteria like Tresca or Hill might be necessary.
- Temperature Dependence: The yield strength of materials varies with temperature. The von Mises stress should be considered in conjunction with temperature-dependent material properties for accurate failure prediction.
Conclusion
Understanding the concept of von Mises stress is fundamental for engineers and scientists working with materials under complex loading conditions. This simplified metric provides a valuable tool for assessing potential yielding and guiding design decisions. However, it is important as well to acknowledge and consider the limitations associated with this criterion for accurate and reliable engineering analysis.