Design of Retaining Walls

In the design of civil engineering structures, retaining walls are normally used to retain soil (earth materials) and possible hydrostatic pressure, and they are usually found on embankments, highways, basements of buildings, etc. This publication presents an example of the design of cantilever retaining walls.

The fundamental requirement of retaining wall design is that the wall must be able to hold the retained material in place without causing excessive movement due to deflection, overturning, or sliding. Furthermore, the wall must be structurally sound to withstand internal stresses such as bending moment and shear due to the retained soil. This is ensured by providing adequate wall thickness and reinforcement.

Retaining wall design can be separated into three basic phases:

(1) Stability analysis – ultimate limit state (EQU and GEO)
(2) Bearing pressure analysis – ultimate limit state (GEO), and
(3) Member design and detailing – ultimate limit state (STR) and serviceability limit states.

Stability Analysis

A retaining wall must be stable under the action of the loads corresponding to the ultimate limit state (EQU) in terms of resistance to overturning. This is exemplified by the straightforward example of a gravity wall shown below.

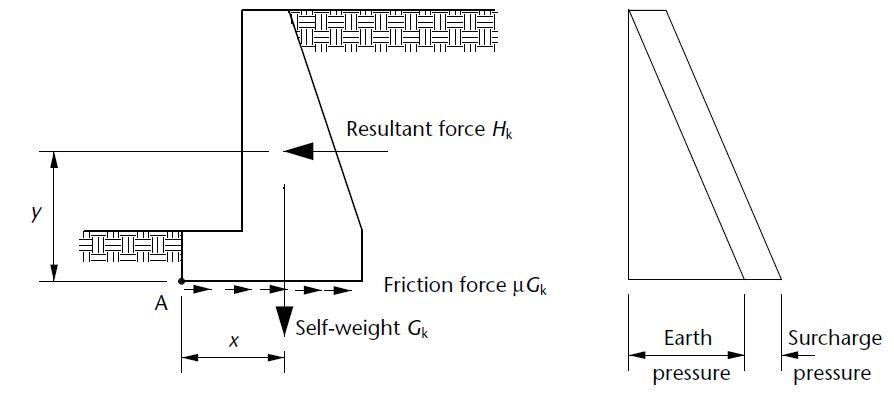
When a maximal horizontal force interacts with a minimal vertical load, overturning becomes critical. It is common practice to apply conservative safety factors of safety to the pressures and weights in order to prevent failure by overturning. The partial factors of safety that are important to these calculations are listed in Table 10.1(c).

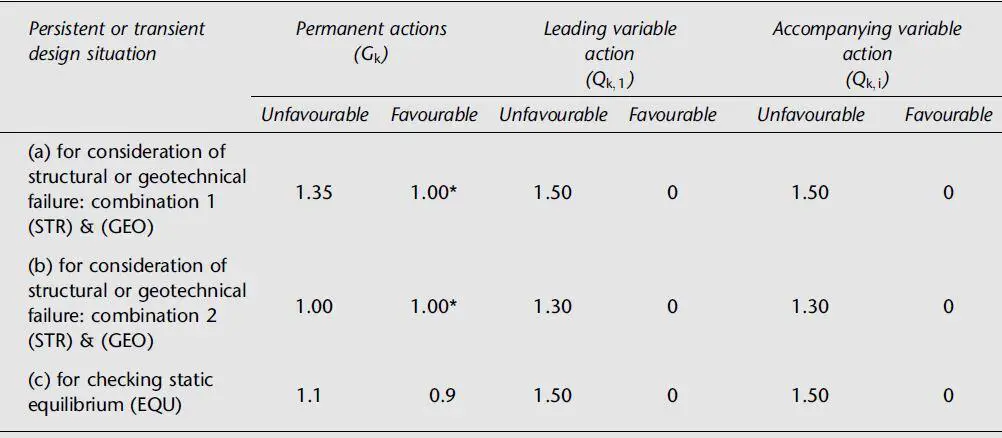
If the permanent load G_k has “favourable” effects, a partial factor of safety of γ_G = 0.9 is applied, and if the effects of the permanent earth pressure loading at the rear face of the wall have “unfavourable” effects, a partial factor of safety of γ_f = 1.1 is multiplied. The variable surcharge loading’s “unfavorable” consequences, if any, are compounded by a partial factor of safety of γ_f = 1.5.

The moment for overturning resistance is normally taken about the toe of the base, at point A on figure 1. Consequently, it is necessary that 0.9G_kx > γ_fH_ky.

Friction between the base’s bottom and the ground provides the resistance to sliding, which is why it is also influenced by the entire self-weight G_k. The base’s front face may experience some resistance from passive ground pressure, but as this material is frequently backfilled against the face, this resistance cannot be guaranteed and is typically disregarded.

Failure by sliding is taken into account while analyzing the loads that correspond to the GEO’s final limit condition. The variables that apply to these calculations are listed in the table above. Typically, it is observed that sliding resistance is usually more critical than overturning. If the sliding requirement is not satisfied, a heel beam may be employed, and the force from passive earth pressure across the heel’s face area may be added to the force resisting sliding.

Bearing Pressure Analysis

When evaluating the necessary foundation size, the bearing pressures behind retaining walls are evaluated using the geotechnical ultimate limit state (GEO). The analysis is comparable to what would happen to a foundation if an eccentric vertical load and an overturning moment were to act simultaneously.

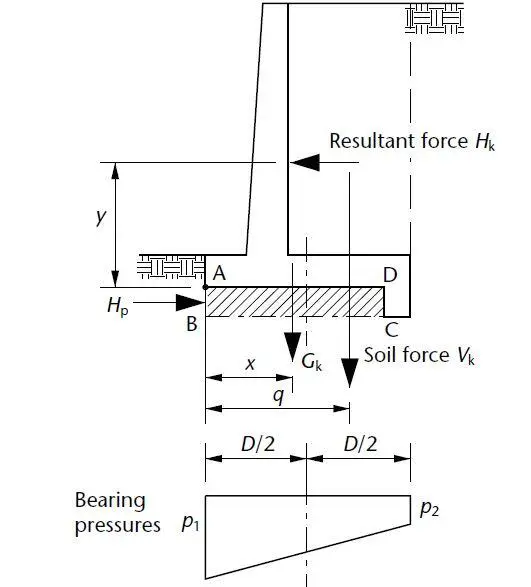
The distribution of bearing pressures will be as shown below, provided the effective eccentricity lies within the ‘middle third’ of the base, that is;

M/P ≤ B/6

Therefore;

p_max = P/B + 6M/B²
p_min = P/B – 6M/B²

In general, section 9 of EN 1997-1 applies to retaining structures supporting ground (i.e. soil, rock or backfill) and/or water and is sub-divided as follows:

§9.1. General
§9.2. Limit states
§9.3. Actions, geometrical data and design situations
§9.4. Design and construction considerations
§9.5. Determination of earth pressures
§9.6. Water pressures
§9.7. Ultimate limit state design
§9.8. Serviceability limit state design

According to EN 1997-1, ultimate limit states GEO and STR must be verified using one of three Design Approaches (DAs). The United Kingdom proposed to adopt Design Approach 1, and this has been used in this design.

The design of gravity walls to Eurocode 7 involves checking that the ground beneath the wall has sufficient:

• bearing resistance to withstand inclined, eccentric actions
• sliding resistance to withstand horizontal and inclined actions
• stability to avoid toppling
• stiffness to prevent unacceptable settlement or tilt

Verification of ultimate limit states (ULSs) is demonstrated by satisfying the inequalities:
V_d ≤ R_d
H_d ≤ R_d
M_Ed,dst ≤ M_Ed,stb

In the example downloadable in this post, the retaining wall shown below has been analysed for resistance against sliding, overturning, and bearing. All the calculations were carried out at ultimate limit state.

Member Design and Detailing

The design of bending and shear reinforcement, like that of foundations, is based on a consideration of the loads for the ultimate limit state (STR), along with the accompanying bearing pressures. Steel will rarely be needed in gravity walls, whereas the walls in counterfort and cantilever walls may be designed as slabs. Unless they are quite large, counterforts often have a cantilever beam-like design.

The stem of a retaining wall of the cantilever type is made to resist the moment brought on by the horizontal forces. The thickness of the wall can be calculated as 80mm per metre of backfill for the purposes of preliminary sizing. In most cases, the base’s thickness is the same with the stem’s. The heel and toe need to be made to resist the moments brought on by the downward weight of the base and soil and the upward earth-bearing pressures.

As necessary, reinforcement details of retaining walls must adhere to the general guidelines for slabs and beams. To prevent shrinkage and thermal cracking, special attention must be paid to the reinforcement’s detailing. Because they typically entail enormous concrete pours, gravity walls are particularly prone to damage. Minimal restrictions on thermal and shrinkage movement should be used. The need for strong soil-base friction, however, negates this in the design of bases, making it impossible to create a sliding layer. Therefore, the bases’ reinforcement needs to be sufficient to prevent cracking from being brought on by a lot of constraint.

Due to the loss of hydration heat during thermal movement, long retaining walls supported by inflexible bases are especially prone to cracking, thus detailing must make an effort to disperse the cracks to maintain appropriate widths. There must be full vertical movement joints available. Waterbars and sealants should be used, and these joints frequently include a shear key to stop differential movement of adjacent wall sections.

Groundwater hydrostatic forces are typically applied to the back sides of retaining walls. By including a drainage passage at the face of the wall, these might be decreased. A layer of earth or porous blocks with pipes to remove the water, frequently through the front of the wall, is the customary method for creating such a drain. Water is less likely to flow through the retaining wall, cause damage to the soil beneath the wall’s foundations, and cause hydrostatic pressure on the wall to decrease as a result.

Retaining Wall Analysis and Design Example

A cantilever retaining wall is loaded as shown below. Design the retaining wall in accordance with EN1997-1:2004 incorporating Corrigendum dated February 2009 and the UK National Annex incorporating Corrigendum No.1.

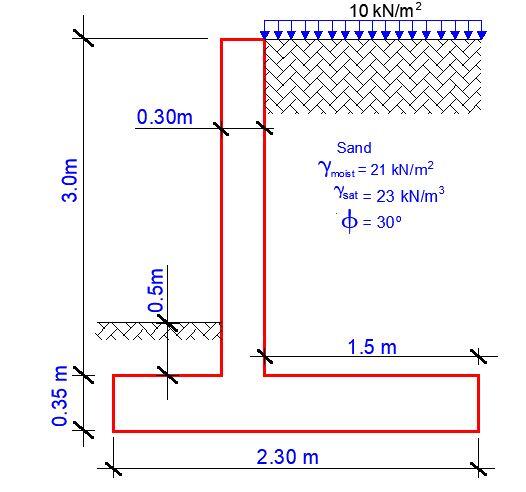
Retaining wall details
Stem type;  Cantilever
Stem height;  h_stem = 3000 mm
Stem thickness; t_stem = 300 mm
Angle to rear face of stem; α = 90 deg
Stem density;  γ_stem = 25 kN/m³
Toe length; l_toe = 500 mm
Heel length;  l_heel = 1500 mm
Base thickness;  t_base = 350 mm
Base density; γ_base = 25 kN/m³
Height of retained soil;  h_ret = 2500 mm
Angle of soil surface; β = 0 deg
Depth of cover; d_cover = 500 mm
Depth of excavation; d_exc = 200 mm

Retained soil properties
Soil type; Medium-dense well graded sand
Moist density; γ_mr = 21 kN/m³
Saturated density; γ_sr = 23 kN/m³
Characteristic effective shear resistance angle; φ’_r.k = 30 deg
Characteristic wall friction angle; δ_r.k = 0 deg

Base soil properties
Soil type; Medium-dense well graded sand
Soil density; γ_b = 18 kN/m³
Characteristic cohesion; c’_b.k = 0 kN/m²
Characteristic effective shear resistance angle; φ’_b.k = 30 deg
Characteristic wall friction angle; δ_b.k = 15 deg
Characteristic base friction angle;  δ_bb.k = 30 deg

Loading details
Variable surcharge load; Surcharge_Q = 10 kN/m²

Retaining wall geometry
Base length; l_base = l_toe + t_stem + l_heel = 2300 mm
Moist soil height;  h_moist = h_soil = 3000 mm
Length of surcharge load; l_sur = l_heel = 1500 mm
– Distance to vertical component;  x_{sur_v} = l_base – (l_heel / 2) = 1550 mm
Effective height of wall; h_eff = h_base + d_cover + h_ret = 3350 mm
– Distance to horizontal component; x_{sur_h} = h_eff / 2 = 1675 mm

Area of wall stem; A_stem = h_stem × t_stem = 0.9 m²
– Distance to vertical component; x_stem = l_toe + t_stem / 2 = 650 mm

Area of wall base; A_base = l_base × t_base = 0.805 m²
– Distance to vertical component; x_base = l_base / 2 = 1150 mm

Area of moist soil;  A_moist = h_moist × l_heel = 4.5 m²
– Distance to vertical component; x_{moist_v} = l_base – (h_moist × l_heel² / 2) / A_moist = 1550 mm
– Distance to horizontal component; x_{moist_h} = h_eff / 3 = 1117 mm

Area of base soil; A_pass = d_cover × l_toe = 0.25 m²
– Distance to vertical component; x_{pass_v} = l_base – [d_cover × l_toe × (l_base – l_toe/2)] / A_pass = 250 mm
– Distance to horizontal component;  x_{pass_h} = (d_cover + h_base) / 3 = 283 mm

Area of excavated base soil; A_exc = h_pass × l_toe = 0.15 m²
– Distance to vertical component; x_{exc_v} = l_base – [h_pass × l_toe × (l_base – l_toe/2)] / A_exc = 250 mm
– Distance to horizontal component;  x_{exc_h} = (h_pass + h_base) / 3 = 217 mm

Design approach 1 – Combination 1

Partial factor set;  A1
Permanent unfavourable action; γ_G = 1.35
Permanent favourable action; γ_Gf = 1.00
Variable unfavourable action; γ_Q = 1.50
Variable favourable action; γ_Qf = 0.00

Partial factors for soil parameters – Table A.4 – Combination 1
Soil parameter set; M1
Angle of shearing resistance;  γ_φ‘ = 1.00
Effective cohesion; γ_c’ = 1.00
Weight density; γ_g = 1.00

Retained soil properties
Design moist density; γ_mr‘ = γ_mr / γ_g = 21 kN/m³
Design saturated density; γ_sr‘ = γ_sr / γ_g = 23 kN/m³
Design effective shear resistance angle; φ’_r.d = tan^-1(tan(φ’_r.k) / γ_φ’) = 30 deg
Design wall friction angle;  δ_r.d = tan^-1(tan(δ_r.k) / γ_φ’) = 0 deg

Base soil properties
Design soil density; γ_b‘ = γ_b/γ_g = 18 kN/m³
Design effective shear resistance angle;  φ’_b.d = tan^-1(tan(φ’_b.k) / γ_φ’) = 30 deg
Design wall friction angle; δ_b.d = tan^-1(tan(δ_b.k) / γ_φ’) = 15 deg
Design base friction angle; δ_bb.d = tan^-1(tan(δ_bb.k) / γ_φ’) = 30 deg
Design effective cohesion; c’_b.d = c’_b.k / γ_c’ = 0 kN/m²

Using Rankine theory
Active pressure coefficient; K_A = (1 – sin(φ’_r.d)) / (1 + sin(φ’_r.d)) = 0.333
Passive pressure coefficient; K_P = (1 + sin(φ’_b.d)) / (1 – sin(φ’_b.d)) = 3.000

Sliding check

Vertical forces on wall
Wall stem; F_stem = γ_Gf × A_stem × γ_stem = 22.5 kN/m
Wall base; F_base = γ_Gf × A_base × γ_base = 20.1 kN/m
Moist retained soil; F_{moist_v} = γ_Gf × A_moist × γ_mr‘ = 94.5 kN/m
Base soil; F_{exc_v} = γ_Gf × A_exc × γ_b‘ = 2.7 kN/m
Total;  F_{total_v} = F_stem + F_base + F_{moist_v} + F_{exc_v} = 139.8 kN/m

Horizontal forces on wall
Surcharge load; F_{sur_h} = K_A × γ_Q × Surcharge_Q × h_eff = 16.8 kN/m
Moist retained soil;F_{moist_h} = γ_G × K_A × γ_mr‘ × h_eff² / 2 = 53 kN/m
Total;  F_{total_h} = F_{sur_h} + F_{moist_h} = 69.8 kN/m

Check stability against sliding
Base soil resistance; F_{exc_h} = γ_GfK_Pγ_b‘ × (h_pass + h_base)² / 2 = 11.4 kN/m
Base friction; F_friction = F_{total_v} × tan(δ_bb.d) = 80.7 kN/m
Resistance to sliding; F_rest = F_{exc_h} + F_friction = 92.1 kN/m

Factor of safety;  FoS_sl = F_rest / F_{total_h} = 1.32

PASS – Resistance to sliding is greater than sliding force

Overturning check

Vertical forces on wall
Wall stem; F_stem = γ_Gf × A_stem × γ_stem = 22.5 kN/m
Wall base;  F_base = γ_Gf × A_base × γ_base = 20.1 kN/m
Moist retained soil;  F_{moist_v} = γ_Gf × A_moist × γ_mr‘ = 94.5 kN/m
Base soil; F_{exc_v} = γ_Gf × A_exc × γ_b‘ = 2.7 kN/m
Total; F_{total_v} = F_stem + F_base + F_{moist_v} + F_{exc_v} = 139.8 kN/m

Horizontal forces on wall
Surcharge load;  F_{sur_h} = K_A × γ_Q × Surcharge_Q × h_eff = 16.8 kN/m
Moist retained soil; F_{moist_h} = γ_G × K_A × γ_mr‘ × h_eff² / 2 = 53 kN/m
Base soil; F_{exc_h} = -γ_Gf × K_P × γ_b‘ × (h_pass + h_base)² / 2 = -11.4 kN/m
Total;  F_{total_h} = F_{sur_h} + F_{moist_h} + F_{exc_h} = 58.4 kN/m

Overturning moments on wall
Surcharge load; M_{sur_OT} = F_{sur_h} × x_{sur_h} = 28.1 kNm/m
Moist retained soil; M_{moist_OT} = F_{moist_h} × x_{moist_h} = 59.2 kNm/m
Total;  M_{total_OT} = M_{sur_OT} + M_{moist_OT} = 87.3 kNm/m

Restoring moments on wall
Wall stem; M_{stem_R} = F_stem × x_stem = 14.6 kNm/m
Wall base; M_{base_R} = F_base × x_base = 23.1 kNm/m
Moist retained soil; M_{moist_R} = F_{moist_v} × x_{moist_v} = 146.5 kNm/m
Base soil; M_{exc_R} = F_{exc_v} × x_{exc_v} – F_{exc_h} × x_{exc_h} = 3.1 kNm/m
Total;  M_{total_R} = M_{stem_R} + M_{base_R} + M_{moist_R} + M_{exc_R} = 187.4 kNm/m

Check stability against overturning
Factor of safety; FoS_ot = M_{total_R} / M_{total_OT} = 2.147

PASS – Maximum restoring moment is greater than the overturning moment

Bearing pressure check

Vertical forces on wall
Wall stem;  F_stem = γ_G × A_stem × γ_stem = 30.4 kN/m
Wall base;  F_base = γ_G × A_base × γ_base = 27.2 kN/m
Surcharge load; F_{sur_v} = γ_Q × Surcharge_Q × l_heel = 22.5 kN/m
Moist retained soil; F_{moist_v} = γ_G × A_moist × γ_mr‘ = 127.6 kN/m
Base soil; F_{pass_v} = γ_G × A_pass × γ_b‘ = 6.1 kN/m
Total;  F_{total_v} = F_stem + F_base + F_{sur_v} + F_{moist_v} + F_{pass_v} = 213.7 kN/m

Horizontal forces on wall
Surcharge load; F_{sur_h} = K_A × γ_Q × Surcharge_Q × h_eff = 16.8 kN/m
Moist retained soil; F_{moist_h} = γ_G × K_A × γ_mr‘ × h_eff² / 2 = 53 kN/m
Base soil;  F_{pass_h} = -γ_Gf × K_P × γ_b‘ × (d_cover + h_base)² / 2 = -19.5 kN/m
Total;   F_{total_h} = max(F_{sur_h} + F_{moist_h} + F_{pass_h} – F_{total_v} × tan(d_bb.d), 0 kN/m) = 0 kN/m

Moments on wall
Wall stem;  M_stem = F_stem × x_stem = 19.7 kNm/m
Wall base; M_base = F_base × x_base = 31.2 kNm/m
Surcharge load;  M_sur = F_{sur_v} × x_{sur_v} – F_{sur_h} × x_{sur_h} = 6.8 kNm/m
Moist retained soil; M_moist = F_{moist_v} × x_{moist_v} – F_{moist_h} × x_{moist_h} = 138.5 kNm/m
Base soil;  M_pass = F_{pass_v} × x_{pass_v} – F_{pass_h} × x_{pass_h} = 7 kNm/m
Total;  M_total = M_stem + M_base + M_sur + M_moist + M_pass = 203.4 kNm/m

Check bearing pressure
Distance to reaction;  x’ = M_total / F_{total_v} = 952 mm
Eccentricity of reaction;  e = x’ – l_base / 2 = -198 mm
Loaded length of base; l_load = 2x’ = 1903 mm
Bearing pressure at toe; q_toe = F_{total_v} / l_load = 112.3 kN/m²
Bearing pressure at heel; q_heel = 0 kN/m²

Effective overburden pressure; q = (t_base + d_cover)γ_b‘ = 15.3 kN/m²
Design effective overburden pressure; q’ = q / γ_g = 15.3 kN/m²

Bearing resistance factors;                                            
N_q = Exp(π × tan(φ’_b.d)) × (tan(45 deg + φ’_b.d / 2))² = 18.401
N_c = (N_q – 1)cot(φ’_b.d) = 30.14
N_γ = 2(N_q – 1)tan(φ’_b.d) = 20.093

Foundation shape factors;                                             
s_q = 1
s_γ = 1
s_c = 1

Load inclination factors;                                                 
H = F_{sur_h} + F_{moist_h} + F_{pass_h} = 50.3 kN/m
V = F_{total_v} = 213.7 kN/m
m = 2

i_q = [1 – H / (V + l_load × c’_b.d × cot(φ’_b.d))]^m = 0.585
i_γ = [1 – H / (V + l_load × c’_b.d × cot(φ’_b.d))]^{(m + 1)} = 0.447
i_c = i_q – (1 – i_q) / (N_c × tan(φ’_b.d)) = 0.561

Net ultimate bearing capacity
n_f = c’_b.dN_cs_ci_c + q’N_qs_qi_q + 0.5γ_b‘l_loadN_γs_γi_γ = 318.6 kN/m²

Factor of safety;                                                               
FoS_bp = n_f / max(q_toe, q_heel) = 2.838

PASS – Allowable bearing pressure exceeds maximum applied bearing pressure

Design approach 1 – Combination 2

Partial factor set; A2
Permanent unfavourable action; γ_G = 1.00
Permanent favourable action;  γ_Gf = 1.00
Variable unfavourable action;   γ_Q = 1.30
Variable favourable action; γ_Qf = 0.00

Soil parameter set; M2
Angle of shearing resistance; γ_f’ = 1.25
Effective cohesion; γ_c’ = 1.25
Weight density; γ_g = 1.00

Retained soil properties
Design moist density;  γ_mr‘ = γ_mr/γ_g = 21 kN/m³
Design saturated density; γ_sr‘ = γ_sr/γ_g = 23 kN/m³
Design effective shear resistance angle; φ’_r.d = tan^-1(tan(φ’_r.k) / γ_φ’) = 24.8 deg
Design wall friction angle; δ_r.d = tan^-1(tan(δ_r.k) / γ_φ’) = 0 deg

Base soil properties
Design soil density;  γ_b‘ = γ_b/γ_g = 18 kN/m³
Design effective shear resistance angle;   φ’_b.d = tan^-1(tan(φ’_b.k) / γ_φ’) = 24.8 deg
Design wall friction angle; δ_b.d = tan^-1(tan(δ_b.k) / γ_φ’) = 12.1 deg
Design base friction angle;  δ_bb.d = tan^-1(tan(δ_bb.k) / γ_φ’) = 24.8 deg
Design effective cohesion;  c’_b.d = c’_b.k /γ_c’ = 0 kN/m²

Using Rankine theory
Active pressure coefficient;                                           
K_A = (1 – sin(φ’_r.d)) / (1 + sin(φ’_r.d)) = 0.409

Passive pressure coefficient;                                        
K_P = (1 + sin(φ’_b.d)) / (1 – sin(φ’_b.d)) = 2.444

Sliding check

Vertical forces on wall
Wall stem; F_stem = γ_Gf × A_stem × γ_stem = 22.5 kN/m
Wall base;  F_base = γ_Gf × A_base × γ_base = 20.1 kN/m
Moist retained soil;F_{moist_v} = γ_Gf × A_moist × γ_mr‘ = 94.5 kN/m
Base soil;F_{exc_v} = γ_Gf × A_exc × γ_b‘ = 2.7 kN/m
Total; F_{total_v} = F_stem + F_base + F_{moist_v} + F_{exc_v} = 139.8 kN/m

Horizontal forces on wall
Surcharge load;  F_{sur_h} = K_A × γ_Q × Surcharge_Q × h_eff = 17.8 kN/m
Moist retained soil;  F_{moist_h} = γ_G × K_A × γ_mr‘ × h_eff² / 2 = 48.2 kN/m
Total;  F_{total_h} = F_{sur_h} + F_{moist_h} = 66 kN/m

Check stability against sliding
Base soil resistance; F_{exc_h} = γ_Gf × K_P × γ_b‘ × (h_pass + h_base)² / 2 = 9.3 kN/m
Base friction; F_friction = F_{total_v} × tan(d_bb.d) = 64.6 kN/m
Resistance to sliding;  F_rest = F_{exc_h} + F_friction = 73.9 kN/m

Factor of safety; FoS_sl = F_rest / F_{total_h} = 1.119

PASS – Resistance to sliding is greater than sliding force

Overturning check

Vertical forces on wall
Wall stem;  F_stem = γ_Gf × A_stem × γ_stem = 22.5 kN/m
Wall base;  F_base = γ_Gf × A_base × γ_base = 20.1 kN/m
Moist retained soil;  F_{moist_v} = γ_Gf × A_moist × γ_mr‘ = 94.5 kN/m
Base soil;  F_{exc_v} = γ_Gf × A_exc × γ_b‘ = 2.7 kN/m
Total;  F_{total_v} = F_stem + F_base + F_{moist_v} + F_{exc_v} = 139.8 kN/m

Horizontal forces on wall
Surcharge load; F_{sur_h} = K_A × γ_Q × Surcharge_Q × h_eff = 17.8 kN/m
Moist retained soil; F_{moist_h} = γ_G × K_A × γ_mr‘ × h_eff² / 2 = 48.2 kN/m
Base soil; F_{exc_h} = -γ_Gf × K_P × γ_b‘ × (h_pass + h_base)² / 2 = -9.3 kN/m
Total; F_{total_h} = F_{sur_h} + F_{moist_h} + F_{exc_h} = 56.7 kN/m

Overturning moments on wall
Surcharge load; M_{sur_OT} = F_{sur_h} × x_{sur_h} = 29.8 kNm/m
Moist retained soil;  M_{moist_OT} = F_{moist_h} × x_{moist_h} = 53.8 kNm/m
Total; M_{total_OT} = M_{sur_OT} + M_{moist_OT} = 83.7 kNm/m

Restoring moments on wall
Wall stem; M_{stem_R} = F_stem × x_stem = 14.6 kNm/m
Wall base;  M_{base_R} = F_base × x_base = 23.1 kNm/m
Moist retained soil; M_{moist_R} = F_{moist_v} × x_{moist_v} = 146.5 kNm/m
Base soil; M_{exc_R} = F_{exc_v} × x_{exc_v} – F_{exc_h} × x_{exc_h} = 2.7 kNm/m
Total; M_{total_R} = M_{stem_R} + M_{base_R} + M_{moist_R} + M_{exc_R} = 186.9 kNm/m

Check stability against overturning
Factor of safety; FoS_ot = M_{total_R} / M_{total_OT} = 2.234

PASS – Maximum restoring moment is greater than overturning moment

Bearing pressure check

Vertical forces on wall
Wall stem; F_stem = γ_G × A_stem × γ_stem = 22.5 kN/m
Wall base; F_base = γ_G × A_base × γ_base = 20.1 kN/m
Surcharge load;  F_{sur_v} = γ_Q × Surcharge_Q × l_heel = 19.5 kN/m
Moist retained soil; F_{moist_v} = γ_G × A_moist × γ_mr‘ = 94.5 kN/m
Base soil; F_{pass_v} = γ_G × A_pass × γ_b‘ = 4.5 kN/m
Total; F_{total_v} = F_stem + F_base + F_{sur_v} + F_{moist_v} + F_{pass_v} = 161.1 kN/m

Horizontal forces on wall
Surcharge load; F_{sur_h} = K_A × γ_Q × Surcharge_Q × h_eff = 17.8 kN/m
Moist retained soil;  F_{moist_h} = γ_G × K_A × γ_mr‘ × h_eff² / 2 = 48.2 kN/m
Base soil; F_{pass_h} = -γ_Gf × K_P × γ_b‘ × (d_cover + h_base)² / 2 = -15.9 kN/m
Total; F_{total_h} = max(F_{sur_h} + F_{moist_h} + F_{pass_h} – F_{total_v} × tan(δ_bb.d), 0 kN/m) = 0 kN/m

Moments on wall
Wall stem; M_stem = F_stem × x_stem = 14.6 kNm/m
Wall base;  M_base = F_base × x_base = 23.1 kNm/m
Surcharge load; M_sur = F_{sur_v} × x_{sur_v} – F_{sur_h} × x_{sur_h} = 0.4 kNm/m
Moist retained soil; M_moist = F_{moist_v} × x_{moist_v} – F_{moist_h} × x_{moist_h} = 92.6 kNm/m
Base soil; M_pass = F_{pass_v} × x_{pass_v} – F_{pass_h} × x_{pass_h} = 5.6 kNm/m
Total; M_total = M_stem + M_base + M_sur + M_moist + M_pass = 136.4 kNm/m

Check bearing pressure
Distance to reaction; x’ = M_total / F_{total_v} = 847 mm
Eccentricity of reaction;  e = x’ – l_base / 2 = -303 mm
Loaded length of base; l_load = 2x’ = 1693 mm
Bearing pressure at toe; q_toe = F_{total_v} / l_load = 95.2 kN/m²
Bearing pressure at heel; q_heel = 0 kN/m²

Effective overburden pressure; q = (t_base + d_cover)γ_b‘ = 15.3 kN/m²

Design effective overburden pressure; q’ = q/γ_g = 15.3 kN/m²

Bearing resistance factors;                                            
N_q = Exp[πtan(φ’_b.d)] × [tan(45 deg + φ’_b.d / 2)]² = 10.431
N_c = (N_q – 1) × cot(φ’_b.d) = 20.418
N_γ = 2(N_q – 1) × tan(φ’_b.d) = 8.712

Foundation shape factors;                                             
s_q = 1
s_γ = 1
s_c = 1

Load inclination factors;                                                 
H = F_{sur_h} + F_{moist_h} + F_{pass_h} = 50.1 kN/m
V = F_{total_v} = 161.1 kN/m
m = 2

i_q = [1 – H / (V + l_load × c’_b.d × cot(φ’_b.d))]^m = 0.475
i_γ = [1 – H / (V + l_load × c’_b.d × cot(f’φ_b.d))]^{(m + 1)} = 0.327
i_c = i_q – (1 – i_q) / (N_c × tan(φ’_b.d)) = 0.419

Net ultimate bearing capacity
n_f = c’_b.dN_cs_ci_c + q’N_qs_qi_q + 0.5γ_b‘l_load N_γs_γi_γ = 119.1 kN/m²

Library item: Drained bearing output

Factor of safety;                                                               
FoS_bp = n_f / max(q_toe, q_heel) = 1.252

PASS – Allowable bearing pressure exceeds maximum applied bearing pressure

Analysis summary

Description	Unit	Capacity	Applied	F o S	Result
Sliding stability	kN/m	73.9	66	1.119	PASS
Overturning stability	kNm/m	187.4	87.3	2.147	PASS
Bearing pressure	kN/m2	119.1	95.2	1.252	PASS

Structural Design

In accordance with EN1992-1-1:2004 incorporating Corrigendum dated January 2008 and the UK National Annex incorporating National Amendment No.1

Concrete details

Concrete strength class; C20/25
Characteristic compressive cylinder strength; f_ck = 20 N/mm²
Characteristic compressive cube strength; f_ck,cube = 25 N/mm²
Mean value of compressive cylinder strength; f_cm = f_ck + 8 N/mm² = 28 N/mm²
Mean value of axial tensile strength; f_ctm = 0.3(f_ck)^2/3 = 2.2 N/mm²
5% fractile of axial tensile strength;  f_ctk,0.05 = 0.7f_ctm = 1.5 N/mm²
Secant modulus of elasticity of concrete; E_cm = 22 kN/mm²(f_cm/10)^0.3 = 29962 N/mm²
Partial factor for concrete – Table 2.1N; γ_C = 1.50
Compressive strength coefficient – cl.3.1.6(1); a_cc = 0.85
Design compressive concrete strength – exp.3.15;    f_cd = a_cc(f_ck/γ_C) = 11.3 N/mm²
Maximum aggregate size; h_agg = 20 mm
Ultimate strain – Table 3.1;  ε_cu2 = 0.0035
Shortening strain – Table 3.1; ε_cu3 = 0.0035
Effective compression zone height factor; λ = 0.80

Effective strength factor;  h = 1.00
Bending coefficient k₁; K₁ = 0.40
Bending coefficient k₂; K₂ = 1.00(0.6 + 0.0014/ε_cu2) = 1.00
Bending coefficient k₃; K₃ =0.40
Bending coefficient k₄;  K₄ = 1.00(0.6 + 0.0014/ε_cu2) =1.00

Reinforcement details
Characteristic yield strength of reinforcement; f_yk = 500 N/mm²
Modulus of elasticity of reinforcement;  E_s = 200000 N/mm²
Partial factor for reinforcing steel – Table 2.1N; γ_S = 1.15
Design yield strength of reinforcement;  f_yd = f_yk / γ_S = 435 N/mm²

Cover to reinforcement
Front face of stem; c_sf = 40 mm
Rear face of stem;  c_sr = 50 mm
Top face of base;   c_bt = 50 mm
Bottom face of base; c_bb = 75 mm

Check stem design at base of stem

Depth of section; h = 300 mm

Flexural Design (Bending)

Design bending moment combination 1;
M = 65 kNm/m                                 
d = h – c_sr – φ_sr / 2 = 244 mm
K = M / (d²f_ck) = 0.055
K’ = (2h a_cc/γ_C) × [1 – λ(d – K₁)/(2K₂)] × [λ(d – K₁)/(2K₂)]
K’ = 0.207

K’ > K – No compression reinforcement is required

Lever arm;  z = min(0.5 + 0.5(1 – 2K / (h × a_cc / γ_C))^0.5, 0.95)d = 232 mm

Depth of neutral axis; x = 2.5(d – z) = 31 mm

Area of tension reinforcement required; A_sr.req = M / (f_ydz) = 646 mm²/m
Tension reinforcement provided; 12 dia.bars @ 150 c/c ( A_sr.prov = 754 mm²/m)
Minimum area of reinforcement – exp.9.1N; A_sr.min = max(0.26f_ctm / f_yk, 0.0013)d = 317 mm²/m
Maximum area of reinforcement – cl.9.2.1.1(3);A_sr.max = 0.04h = 12000 mm²/m
max(A_sr.req, A_sr.min) / A_sr.prov = 0.856

PASS – Area of reinforcement provided is greater than area of reinforcement required

Deflection control

Reference reinforcement ratio; ρ₀ = √(f_ck) / 1000 = 0.004
Required tension reinforcement ratio; ρ = A_sr.req / d = 0.003
Required compression reinforcement ratio; ρ’ = A_sr.2.req / d₂ = 0.000
Structural system factor – Table 7.4N; K_b = 0.4
Reinforcement factor – exp.7.17; K_s = min(500 / (f_ykA_sr.req / A_sr.prov), 1.5) = 1.168

Limiting span to depth ratio – exp.7.16.a; 
min(K_sK_b[11 + 1.5 × √(f_ck) ρ₀/ρ + 3.2√(f_ck) × (ρ₀/ρ – 1)^3/2], 40K_b) = 14.3

Actual span to depth ratio; h_stem / d = 12.3

PASS – Span to depth ratio is less than deflection control limit

Rectangular section in shear

Design shear force; V = 57.5 kN/m
C_Rd,c = 0.18 / γ_C = 0.120
k = min(1 + √(200 mm / d), 2) = 1.905

Longitudinal reinforcement ratio; ρ_l = min(A_sr.prov / d, 0.02) = 0.003
v_min = 0.035k^3/2f_ck^0.5 = 0.412 N/mm²

Design shear resistance – exp.6.2a & 6.2b;                
V_Rd.c = max(C_Rd.ck(100ρ_lf_ck)^1/3, v_min)d
V_Rd.c = 102.4 kN/m
V / V_Rd.c = 0.562

PASS – Design shear resistance exceeds design shear force

Horizontal reinforcement parallel to face of stem – Section 9.6

Minimum area of reinforcement – cl.9.6.3(1);             
A_sx.req = max(0.25A_sr.prov, 0.001t_stem) = 300 mm²/m
Maximum spacing of reinforcement – cl.9.6.3(2); s_{sx_max} = 400 mm
Transverse reinforcement provided; H10 dia.bars @ 200 c/c (A_sx.prov = 393 mm²/m)

PASS – Area of reinforcement provided is greater than area of reinforcement required

Check base design at toe

Depth of section;  h = 350 mm

Rectangular section in flexure

Design bending moment combination 1;                     
M = 13.8 kNm/m

d = h – c_bb – φ_bb / 2 = 269 mm
K = M / (d² f_ck) = 0.010
K’ = (2h × a_cc/γ_C) × (1 – λ(d – K₁)/(2K₂)) × (λ(d – K₁)/(2K₂))
K’ = 0.207

K’ > K – No compression reinforcement is required

Lever arm;                                                                        
z = min(0.5 + 0.5(1 – 2K / (h × a_cc/γ_C))^0.5, 0.95)d = 256 mm
Depth of neutral axis; x = 2.5(d – z) = 34 mm

Area of tension reinforcement required; A_bb.req = M / (f_ydz) = 124 mm²/m
Tension reinforcement provided;                                 
12 dia.bars @ 200 c/c ( A_bb.prov = 565 mm²/m)

Minimum area of reinforcement – exp.9.1N;               
A_bb.min = max(0.26f_ctm/f_yk, 0.0013)d = 350 mm²/m

Maximum area of reinforcement – cl.9.2.1.1(3);         
A_bb.max = 0.04h = 14000 mm²/m
max(A_bb.req, A_bb.min) / A_bb.prov = 0.618

PASS – Area of reinforcement provided is greater than area of reinforcement required

Rectangular section in shear

Design shear force;                                                         
V = 53.3 kN/m
C_Rd,c = 0.18/γ_C = 0.120
k = min(1 + √(200 mm / d), 2) = 1.862

Longitudinal reinforcement ratio; ρ_l = min(A_bb.prov / d, 0.02) = 0.002

v_min = 0.035 k^3/2f_ck^0.5 = 0.398 N/mm²

Design shear resistance – exp.6.2a & 6.2b;                
V_Rd.c = max(C_Rd.ck(100ρ_lf_ck)^1/3, v_min) d
V_Rd.c = 107 kN/m
V / V_Rd.c = 0.498

PASS – Design shear resistance exceeds design shear force

Check base design at heel

Depth of section; h = 350 mm

Rectangular section in flexure

Design bending moment combination 1;                     
M = 51.9 kNm/m

d = h – c_bt – φ_bt / 2 = 294 mm
K = M / (d²f_ck) = 0.030
K’ = (2h × α_cc/γ_C) × (1 – λ(d – K₁)/(2K₂)) × (λ(d – K₁)/(2K₂))
K’ = 0.207

K’ > K – No compression reinforcement is required

Lever arm;  z = min(0.5 + 0.5(1 – 2K/(h × α_cc/γ_C))^0.5, 0.95)d = 279 mm
Depth of neutral axis;  x = 2.5(d – z) = 37 mm

Area of tension reinforcement required;                     
A_bt.req = M / (f_ydz) = 427 mm²/m

Tension reinforcement provided;                                 
12 dia.bars @ 200 c/c (A_bt.prov = 565 mm²/m)

Minimum area of reinforcement – exp.9.1N;               
A_bt.min = max(0.26f_ctm/f_yk, 0.0013)d = 382 mm²/m

Maximum area of reinforcement – cl.9.2.1.1(3);         
A_bt.max = 0.04h = 14000 mm²/m
max(A_bt.req, A_bt.min) / A_bt.prov = 0.755

PASS – Area of reinforcement provided is greater than area of reinforcement required

Rectangular section in shear

Design shear force;                                                         
V = 53.5 kN/m
C_Rd,c = 0.18 / γ_C = 0.120
k = min(1 + √(200 mm / d), 2) = 1.825

Longitudinal reinforcement ratio;                                  
ρ_l = min(A_bt.prov / d, 0.02) = 0.002
v_min = 0.035k^3/2f_ck^0.5 = 0.386 N/mm²

Design shear resistance – exp.6.2a & 6.2b;                
V_Rd.c = max(C_Rd.ck (100 ρ_lf_ck)^1/3, v_min)d
V_Rd.c = 113.4 kN/m
V / V_Rd.c = 0.472

PASS – Design shear resistance exceeds design shear force

Secondary transverse reinforcement to base – Section 9.3
Minimum area of reinforcement – cl.9.3.1.1(2);         
A_bx.req = 0.2A_bb.prov = 113 mm²/m

Maximum spacing of reinforcement – cl.9.3.1.1(3);   
s_{bx_max} = 450 mm

Transverse reinforcement provided;                            
10 dia.bars @ 200 c/c (A_bx.prov = 393 mm²/m)

PASS – Area of reinforcement provided is greater than area of reinforcement required

Summary

Description	Unit	Provided	Required	Utilisation	Result
Stem ρ0 rear face – Flexural reinforcement	mm2/m	754.0	645.7	0.86	PASS
Stem ρ0 – Shear resistance	kN/m	102.4	57.5	0.56	PASS
Base top face – Flexural reinforcement	mm2/m	565.5	427.2	0.76	PASS
Base bottom face – Flexural reinforcement	mm2/m	565.5	349.7	0.62	PASS
Base – Shear resistance	kN/m	107.0	53.3	0.50	PASS
Transverse stem reinforcement	mm2/m	392.7	300.0	0.76	PASS
Transverse base reinforcement	mm2/m	392.7	113.1	0.29	PASS