Load Balancing in Post-tensioned Two-Way Slab Systems

Load balancing is the most typical approach used in post-tensioned slab design for determining the amount and distribution of prestress after the selection of the initial slab thickness. During the load balancing, a portion of the load is balanced out by the transverse loads that the draped tendons in each direction impose on a slab.

Under the balanced load, the slab remains flat (without curvature) and is only susceptible to the ensuing longitudinal compressive P/A stresses. When assessing service load behaviour, particularly when predicting load-dependent deflections and figuring out how much cracking has occurred and how much crack control has been applied, consideration is given to the remaining imbalanced load.

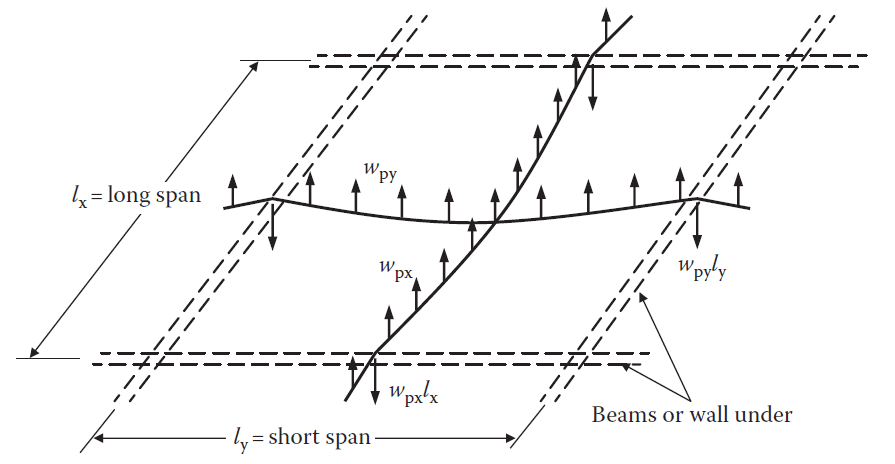
Consider the interior panel of the two-way edge-supported slab shown in Figure 1. The panel has parabolic tendons in both the x and y axes and is supported by walls or beams on all sides. The upward forces per unit area that the tendons in each direction exert if the cables are uniformly spaced in each direction are;

w_px = 8P_xz_d.x/l_x² ——— (1)

and

w_py = 8P_yz_d.y/l_y² ——— (2)

where P_x and P_y are the prestressing forces in each direction per unit width, and z_d.x and z_d.y are the cable drapes in each direction.

The uniformly distributed downward load to be balanced per unit area w_bal is calculated as:

w_bal = w_px + w_py ——— (3)

In practice, perfect load balancing is not possible, since external loads are rarely perfectly uniformly distributed. However, for practical purposes, adequate load balancing can be achieved (Gilbert et al, 2017). Any combination of w_px and w_py that satisfies Equation (3) can be used to make up the balanced load. The smallest quantity of prestressing steel will result if all the loads are balanced by cables in the short-span direction, i.e. w_bal = w_py.

However, under unbalanced loads, serviceability problems in the form of unsightly cracking may result. It is often preferable to distribute the prestress in much the same way as the load is distributed to the supports in an elastic slab, i.e. more prestress in the short-span direction than in the long-span direction. The balanced load resisted by tendons in the short direction may be estimated by:

w_py = [l_x⁴/(δl_y⁴ + l_x⁴)] × w_bal ——— (4)

where δ depends on the support conditions and is given by:

δ = 1.0 for 4 edges continuous or discontinuous
= 1.0 for 2 adjacent edges discontinuous
= 2.0 for 1 long-edge discontinuous
= 0.5 for 1 short edge discontinuous
= 2.5 for 2 long + 1 short edge discontinuous
= 0.4 for 2 short + 1 long edge discontinuous
= 5.0 for 2 long edges discontinuous
= 0.2 for 2 short edges discontinuous

Equation (4) is the expression obtained for that portion of any external load which is carried in the short-span direction if twisting moments are ignored and if the mid-span deflections of the two orthogonal unit-wide strips through the slab centre are equated.

With w_px and w_py selected, the prestressing force per unit width in each direction is calculated using Equations (1) and (2) as:

P_x = w_pxl_x²/8z_d.x ——– (5)

and

P_y = w_pyl_y²/8z_d.y ——– (6)

Equilibrium dictates that the downward forces per unit length exerted over each edge support by the reversal of cable curvature (as shown in Figure 1) are:

w_pxl_x (kN/m) carried by the short-span supporting beams or walls
w_pyl_y (kN/m) carried by the long-span supporting beams or walls

The total force imposed by the slab tendons that must be carried by the edge beams is, therefore:

w_pxl_xl_y + w_pyl_yl_x = w_ball_xl_y ——– (7)

and this is equal to the total upward force exerted by the slab cables.

Therefore, for this two-way slab system, to carry the balanced load to the supporting columns, resistance must be provided for twice the total load to be balanced (i.e. the slab tendons must resist w_ball_xl_y and the supporting beams must resist w_ball_xl_y). This requirement is true for all two-way floor systems, irrespective of construction type or material.

At the balanced load condition, when the transverse forces imposed by the cables exactly balance the applied external loads, the slab is subjected only to the compressive stresses imposed by the longitudinal prestress in each direction, i.e. σx = P_x/h and σy = P_y/h, where h is the slab thickness.

Article Source:
Gilbert R. I, Mickleborough N. C., and Ranzi G. (2017): Design of Prestressed Concrete to Eurocode 2 (Second Edition). CRC Press, Taylor and Francis Group.