Recent researches have shown that human beings interact with structural systems undergoing vibration. Initially it was thought that human body is an inert mass during vibration of structures, but studies have proved otherwise. Human-structure interaction is a study which describes the independent human system and structural system working together as a whole. It also studies the vibration of structural systems where people are involved, and how human body responds to structural vibration.
Vibration serviceability issues are becoming increasingly important in structures subjected to crowd action such as foot bridges, galleries, stadiums, places of assembly etc. This is important given the increasing use of slender and aesthetically pleasing elements in structures. It is understood that the excess lateral vibration of the Millennium bridge which caused the bridge to ‘wobble’ on its opening day gave the impetus for researches on how human beings interact with structural vibration.
According to B.R. Ellis [1] who researched on human-structure interaction in the year 1997;
It has occasionally been assumed that the effect of the people is simply that of an added mass on the system, however, both
site and laboratory tests demonstrate that human bodies do not act solely as mass on the structure and show that the problem is somewhat more complex
In an experiment reported by Ji and Ellis [2], the frequency of a beam was tested when it was empty, and compared with when someone was standing on it. The frequency of the bare beam was observed to be 18.68 Hz, while the frequency of the occupied beam was observed to be 20.02 Hz. If the human body acted as an inert mass, the frequency of the human occupied beam would be smaller rather than bigger. It was therefore observed that the human body did not act as an inert mass but as a mass-spring-damper system. This particular discovery formed the basis for the new topic called human-structure interaction.
Modelling human-structure interaction
Two approaches are usually adopted when studying the dynamic property of a human body based on the bio-mechanical method. One approach is to develop the part-body model and the other approach is to develop the whole-body model [3]. In the body part model, the attention is on the local dynamic properties of body parts such as the hands, heads, or the vibration of the soft tissues, under the assumption that the forces acting on the model are already known. However, the whole-body model is concerned with the holistic dynamic property of the body (for example a human standing on a beam subjected to external excitation). In this case, the force acting on the body is unknown in advance and the interaction between the body and the structure occurs [3].
Instead of the single degree of freedom (S-DOF models that have been extensively investigated, it is recommended that human-structure interaction be modelled with two degrees of freedom (2-DOF), where one degree of freedom is for the structure, and the other for the human being. To develop the two degree of freedom system, one approach is to model two separate single degree of freedom systems (one for the structure and one for the human being), and join the two models together to form a 2-DOF. This method is called separative modelling, and has the advantage of being easily reproducible in the laboratory for experiment [3]. On the other hand, when the system is modelled inseparably as a whole, it called integrative modelling.
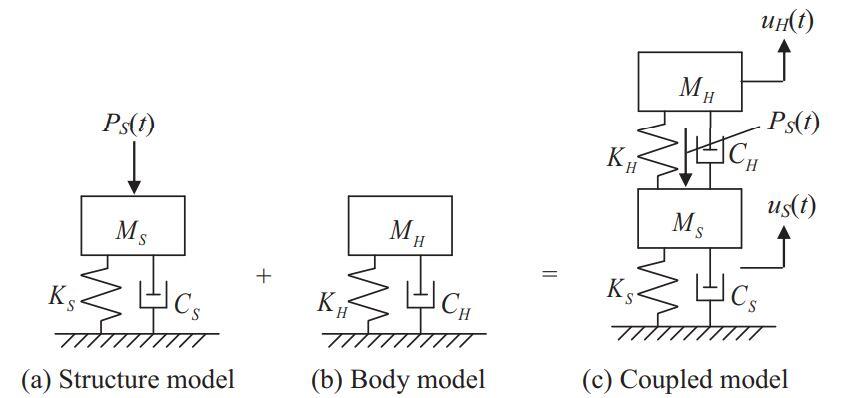
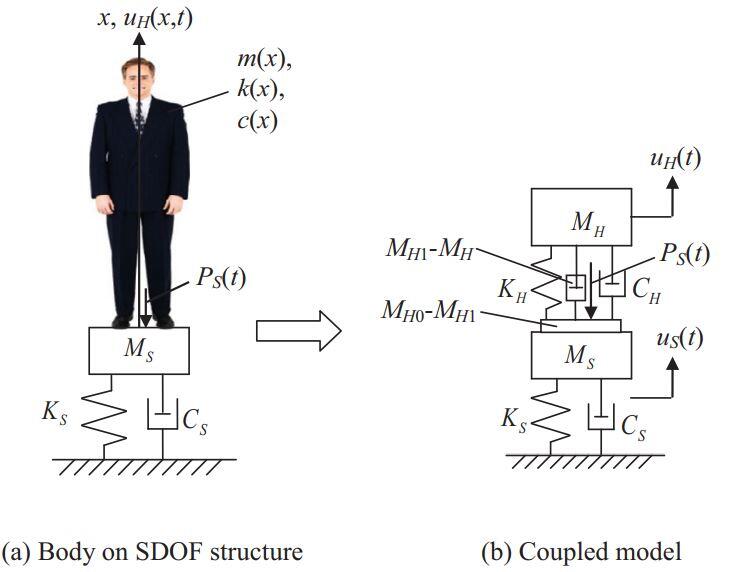
In a parametric research work that was carried out to compare the two models, the natural frequency, damped natural frequency and decrement coefficient of the first mode from the integrative model were found to be smaller than those from the separative model. The authors further concluded that integrative model is more reasonable than the conventional separative model, stating that the separative model can introduce up to 20% error in the calculation of the natural frequency [3].
Applications of human-structure interaction
(1) Prediction of human body response to structural vibration
(2) Evaluate structural vibration where people are involved
(3) Identification of some dynamic characteristics of the human body
(4) Reduction of human induced structural vibrations
(5) Improvement of human comfort in a working environment
(6) Improvement of animal welfare and meat quality
References
[1] Ellis B. R. (1997): Human-structure interactions in vertical vibrations. Proceedings to Institution of Civil Engineers, Structures and Buildings (1997)122 Panel Paper 11023
[2] T. Ji, Ellia B.R: Human-Structure Interaction
[3] Zhou D., Han H., T. Ji, Xu X. (2016): Comparison of two models for human-structure interaction. Applied Mathematical Modelling 40(2016): 3738 – 3748 http://dx.doi.org/10.1016/j.apm.2015.10.049