The famous Maxwell-Mohr’s integral forms the backbone of the force method of structural analysis. It is also an important and universal method of computing displacements in beams and frames. It is more ideal for hand calculation purposes than the direct stiffness method which may involve large matrices.
The Mohr’s integral may be solved by direct multiplication and integration of bending moment equations (one linearly and the other of any arbitrary form), or by using the bending moment diagram multiplication/graphical method which is based on Vereschagin’s rule. Vereschagin’s rule is the graphical solution of Maxwell-Mohr’s integral.
In the paper downloadable in this post, a lot of formulas were derived for combining different shapes of bending moment diagrams for use in the graphical method than can be found in many structural engineering textbooks.
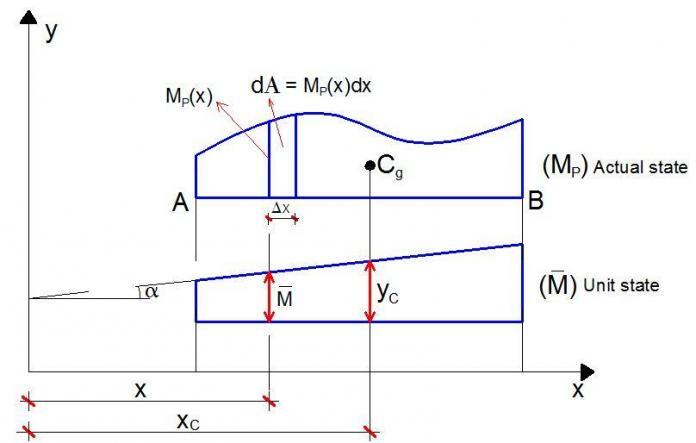
The diagram multiplication method presents the most effective way for computation of any displacement (linear, angular, mutual, etc.) of bending structures, particularly for framed structures. The advantage of this method is that the integration procedure according to Maxwell–Mohr integral is replaced by an elementary algebraic procedure on two bending moment diagrams in the actual and unit states.
This method was developed by Russian engineer Vereschagin in 1925 and is often referred to as the Vereschagin’s rule, in which the area of the bending moment diagram in the actual state multiplies the ordinate that its centroid makes with the unit state diagram in order to obtain the deformation.
READ ALSO ON THIS BLOG…
Example on the Application of Vereschagin’s Rule on the Analysis of Indeterminate Frames
On the Deformation of Statically Indeterminate Frames Using Force Method
In the article, the following examples can be found;
Example 1
The procedure for the combination of the two shapes shown above is presented in the screenshot shown below;
Example 2
In this case, we have to split the shapes at the point of contraflexure, so we have two shapes with areas A1 and A2 combining with the triangle below them. So as usual, we have;
To download the paper the full paper on equation formulation where series of shapes encountered in analysis have been combined, click HERE
To know how Vereschagin’s rule is applied in analysis, click HERE
Visit our facebook page, www.facebook.com/structville