Modal Analysis of Rigid Multi-Storey Frames

A structure undergoes free vibration when it is brought out of static equilibrium and can then oscillate without any external dynamic excitation. Free vibration of structures occurs with some frequencies which depend only on the parameters of the structures such as the boundary conditions, distribution of masses, stiffnesses within the members etc, and not on the reason for the vibration.

At each natural frequency of free vibration, the structure vibrates in simple harmonic motion where the displaced shape (mode shape) of the structure is constant but the amplitude of the displacement is varying in a sinusoidal manner with time. The number of natural frequencies in a structure coincides with the number of degrees of freedom in the structure. These frequencies are inherent to the given structure and are often referred to as eigenfrequencies. Each mode shape of vibration shows the form of an elastic curve which corresponds to a specific frequency.

A method of obtaining the natural frequencies and mode shapes of vibration is modal analysis. This is a technique by which the equations of motion, which are originally expressed in physical coordinates, are transformed to modal coordinates using the eigenvalues and eigenvectors gotten by solving the undamped frequency eigenproblem. The transformed equations are called modal equations.

For an undamped free vibration, the equation of motion is;

Mü + ku = 0 ———-(1)

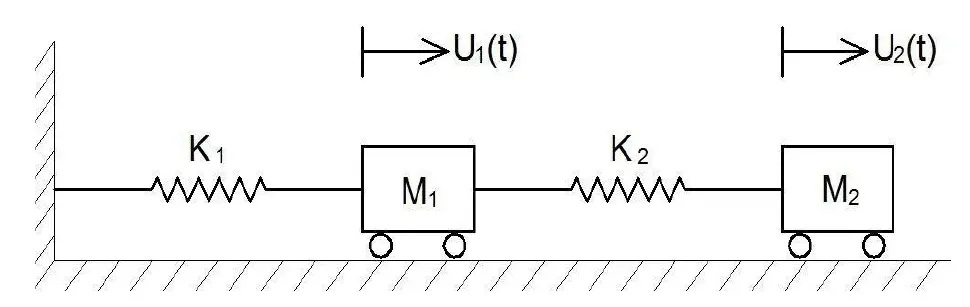
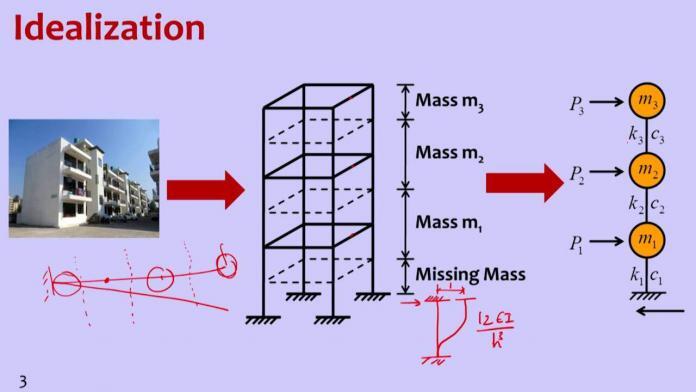
From Figure 1.1, the following equations can be developed;
M₁Ü₁ + K₁U₁ + K₂ (U₁ − U₂) = 0
M₂Ü₂ + K₂(U₂ − U₁) = 0

This can be expanded to give;
M₁Ü₁ + U₁(K₁ + K₂) + U₂(−K₂) = 0
M₂Ü₂ + U₁(-K₂) + U₂(K₂) = 0

Arranging it in matrix form we obtain;

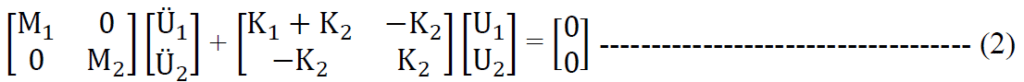
The characteristic polynomial equation is thus;

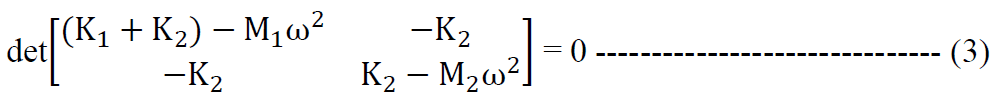
The solution of the equation is;
U₁ = A₁sin(𝜔𝑡+ 𝜑), U₂ = A₂sin(𝜔𝑡+ 𝜑)

Where A_i is the amplitude of the displacement of mass M_i, and 𝜑 is the initial phase of vibration.
[(K₁ + K₂) − M₁ω₂]A₁ − K₂A₂=0
−K₂A₁ + (K₂−M₂ω₂) A₂ = 0

To obtain the frequency equation, a non-trivial solution exists (non-zero amplitudes A_i), if the determinant of the coefficients to the amplitude is zero. This is also called the characteristic polynomial equation and is thus;

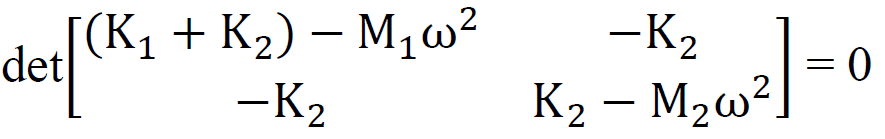
The solution of equation (3) presents the eigenfrequencies of the system. The system does not allow us to determine amplitudes directly, but we can find the ratio between these amplitudes. Hence for equation 3 above;

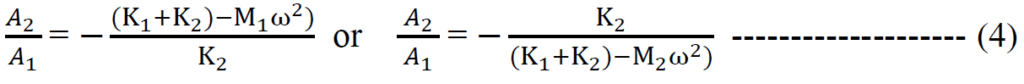
If we assume A₁ = 1.0, then entries [1 𝐴₂]^𝑇 defines for each eigenfrequency, the column 𝜑 of the modal matrix Φ. The shape of each mode of free vibration is unique but the amplitude of the mode shape is undefined. The mode shapes are usually normalised such that the largest term in the vector is 1.0. The mode shapes have the important property of being orthogonal with respect to the mass and stiffness matrix of the structure.

Worked Example

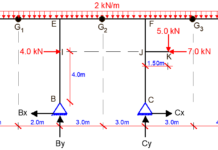
A frame with an infinitely rigid floor is supported by 300 x 300 mm columns. If it is loaded as shown below, carry out the full modal dynamic analysis of the structure. (Take EI = 2.1 × 10⁷ kN/m²)

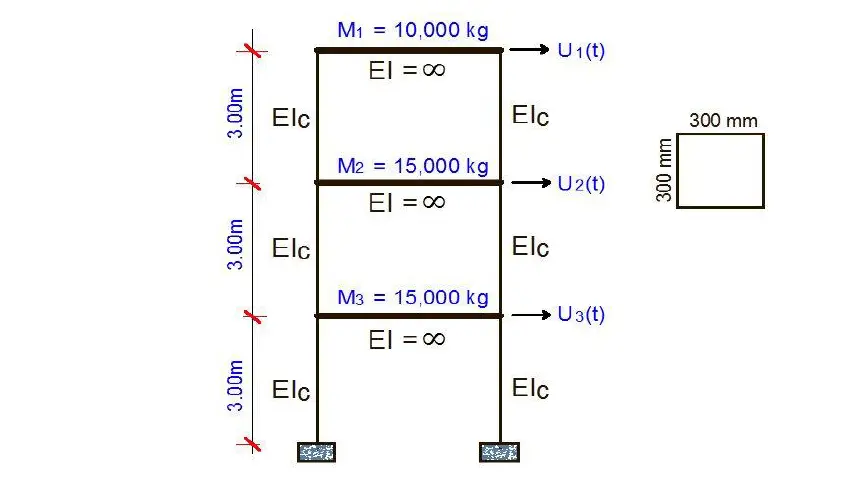
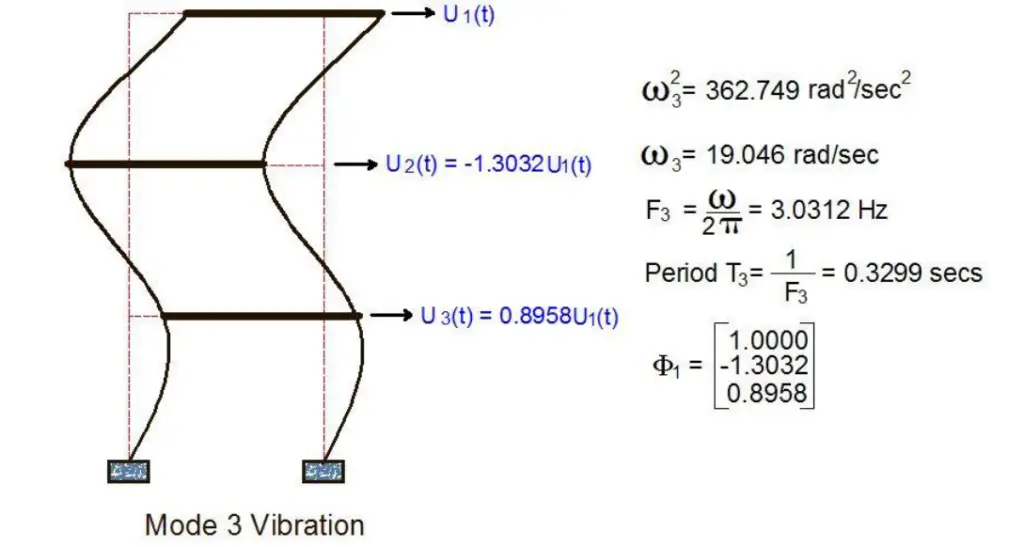
In the paper downloadable in this post, modal dynamic analysis was carried out on the three-storey frame shown above. The results obtained regarding the three assumed degrees of freedom are shown in the pictures below;

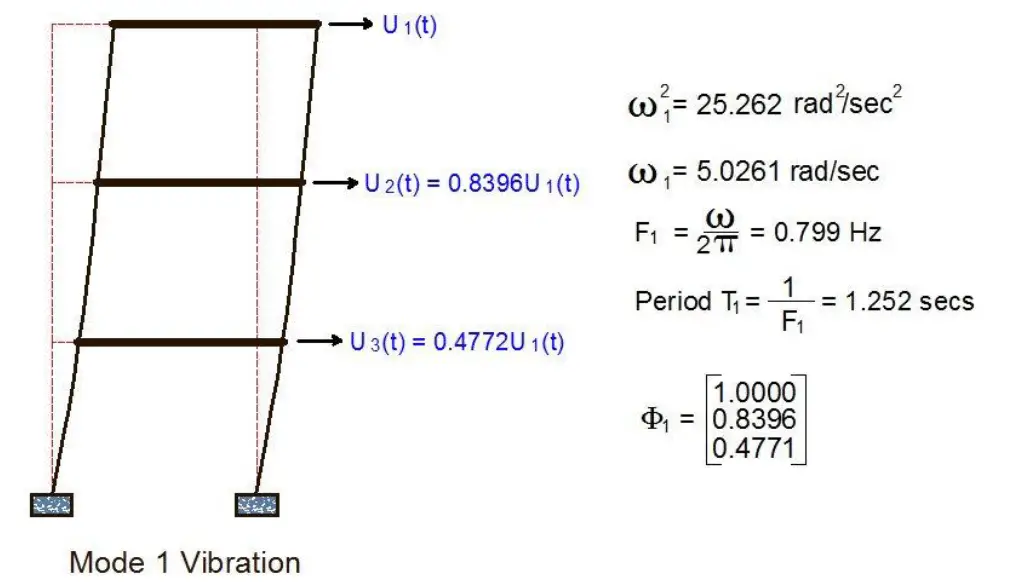
(a) Mode 1 vibration parameters and displaced shape

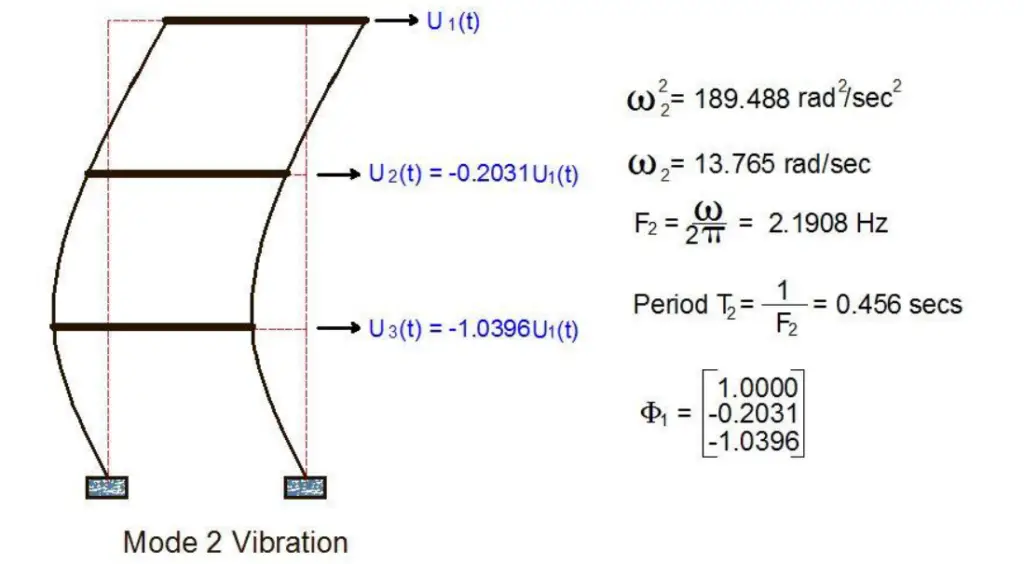
(b) Mode 2 vibration parameters and displaced shape

(c) Mode 3 vibration parameters and displaced shape

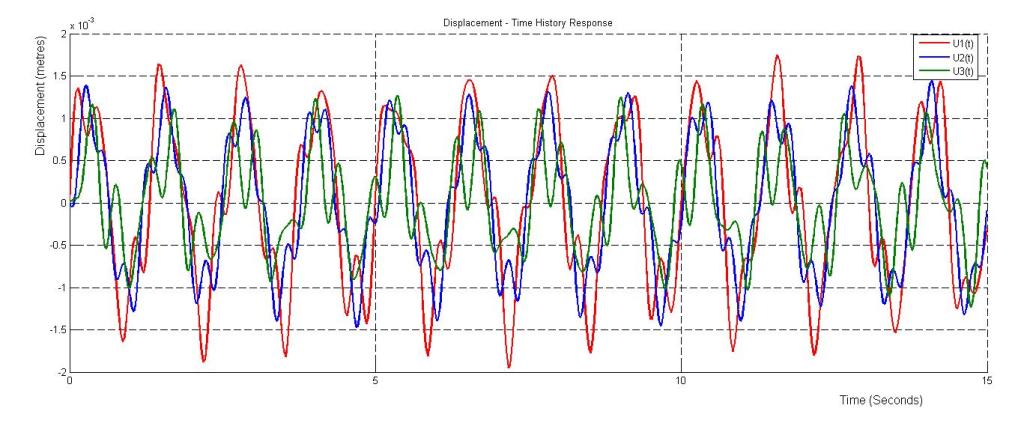
The displacement time history response is therefore;

u₁(t) = 0.00128448 sin(5.0261t) + 0.00044346 sin(13.7654t) + 0.0002408175 sin(19.0459t)

u₂(t) = 0.00107836 sin(5.0261t) – 0.00009 sin(13.7654t) – 0.000313845 sin(19.0459t)

u₃(t) = 0.00061299 sin(5.0261t) – 0.00046104 sin(13.7654t) + 0.0002157225 sin(19.0459t)

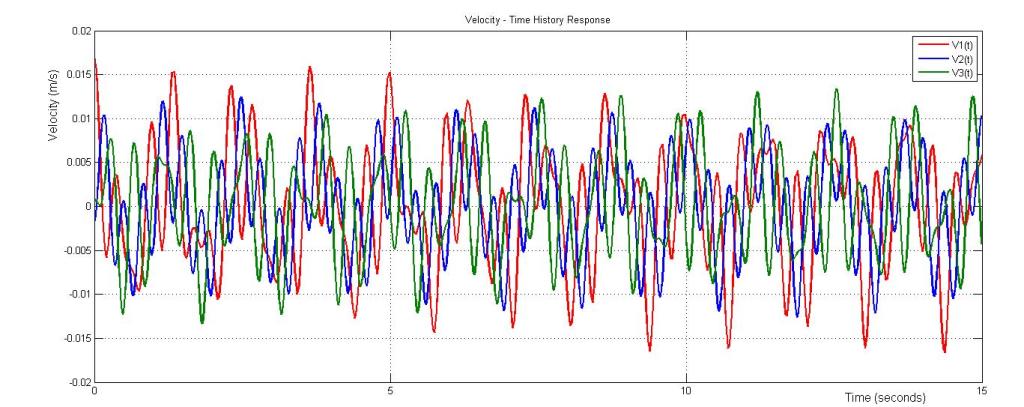
If velocity (v) = du/dt; The velocity time history response is therefore;
The velocity time history response is obtained by direct differentiation of the displacement time history equations;

v₁(t)= 0.0064559 cos(5.0261t) + 0.0061044 cos(13.7654t) + 0.0045865cos(19.0459t)

v₂(t)= 0.0054199 cos(5.0261t) – 0.0012388 cos(13.7654t) – 0.00597746 cos(19.0459t)

v₃(t)= 0.0030809 cos(5.0261t) – 0.0063464 cos(13.7654t) + 0.0041086 cos(19.0459t)

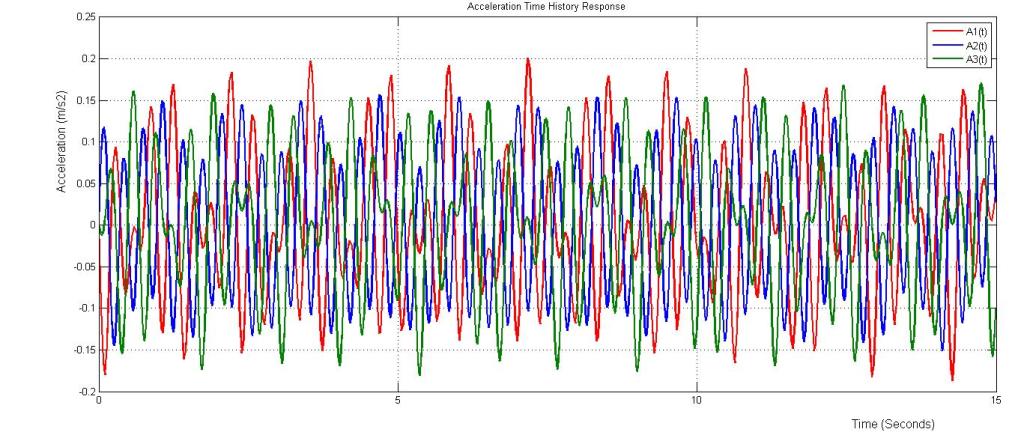
The acceleration (a) time history response is obtained by direct differentiation of the velocity time history equations;

a₁(t) = -0.032448 sin(5.0261t) – 0.0840295 sin(13.7654t) – 0.087354 sin(19.0459t)

a₂(t) = -0.02724 sin(5.0261t) + 0.0170525 sin(13.7654t) + 0.113846 sin(19.0459t)

a₃(t) = -0.0154849 sin(5.0261t) + 0.0873607 sin(13.7654t) – 0.0782519 sin(19.0459t)

To download the full calculation sheet, click HERE.