Design of Doubly Reinforced Beams | Worked Example

Doubly reinforced beams are reinforced concrete beams that incorporate both compression steel (in the compression zone) and tension steel (in the tension zone). This design is typically employed when the required moment capacity of a beam exceeds that which can be provided by singly reinforced beams (those with only tension steel).  

In singly reinforced concrete beams without moment redistribution, k = M_Ed/f_ckbd² is limited to k’ = 0.167. Therefore, once the value of k > k’, the beam must be designed as a doubly reinforced beam. In doubly reinforced beams, compression steel reinforcements are required because the concrete section (in compression) by itself cannot develop the required moment of resistance.

However, when there is a moment redistribution in the section, k > k’ where k’ is dependent on the moment redistribution ratio (δ) and is given by:

k’ = 0.6δ – 0.18δ² – 0.21 where δ ≤ 1.0

In all cases, it is recommended that k’ be limited to 0.167 to ensure ductile failure. It is important to understand that the redistribution of moments derived from elastic analysis of a reinforced concrete structure accounts for the plastic behaviour of the material as it approaches its ultimate limit state.

To facilitate this plastic response, concrete sections must be designed to permit the formation of plastic hinges upon the yielding of tensile reinforcement. This approach ensures a ductile structure characterized by a gradual failure at the ultimate limit state, rather than a sudden, catastrophic collapse due to compressive failure of the concrete.

To guarantee the formation of plastic hinges and the necessary section rotation for ductile behaviour, Eurocode 2 imposes limitations on the maximum neutral axis depth, x_bal. These restrictions ensure that the tensile steel experiences high strains and this promotes the desired plastic response.

The permissible value of x_bal is determined based on the desired degree of moment redistribution. According to Eurocode 2, the limit is x_bal ≤ 0.8(δ – 0.44)d for f_ck ≤ C50. However, this limit was modified to x_bal as x_bal ≤ (δ – 0.4)d in the UK Annex to the EC2.

Design of Doubly Reinforced Beam

To ensure a ductile response and prevent sudden compressive failure of the concrete, it is required that the neutral axis depth should not exceed 0.45 times the effective depth (0.45d). This guideline is typically adopted in the design of sections incorporating compression reinforcement (doubly reinforced beam sections).

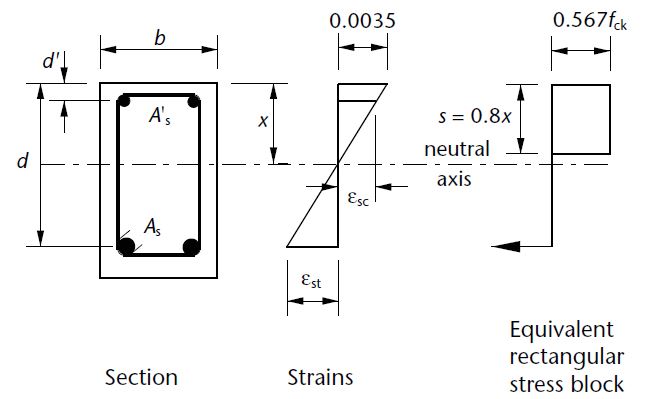
In the design of reinforced concrete beams, if the design ultimate moment is greater than the ultimate moment of resistance i.e. M_Ed > M_lim, then compression reinforcement is required. Provided that d₂/x ≤ 0.38 (i.e. compression steel has yielded) where d₂ is the depth of the compression steel from the compression face and x = (d − z)/0.4

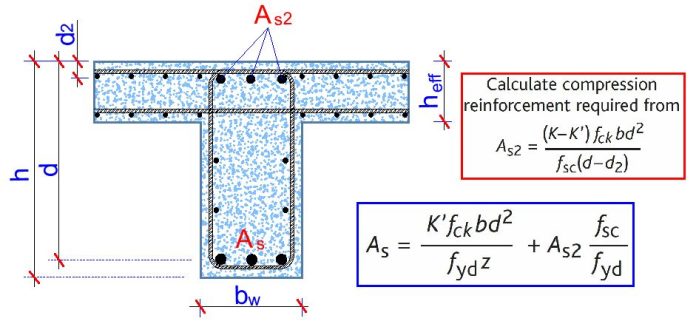
The area of steel in compression, A_s2, is given by:
A_s1 = (M_Ed – M_lim) / (f_sc(d – d₂)) —- (1)
f_sc = E_sε_sc ≤ 0.87f_yk
ε_sc = steel compressive strain = 0.0035(x – d’)/x
E_s = Modulus of elasticity of steel = 200000 N/mm²

Area of tension reinforcement:
A_s1 = M_lim / (0.87f_ykz) + A_s2 (f_sc/0.87f_yk) —- (2)

Where:
M_Ed = Design bending moment of the section
M_lim = 0.167f_ckbd²
z = d[0.5+ √(0.25 – 0.882k’)]
where
k’ = 0.167

Design Example of a Doubly Reinforced Beam

To show how this is done, let us consider the flexural design of support A of the beam loaded as shown below. The depth of the beam is 600 mm, and the width is 400 mm.
f_ck = 35 N/mm² ; f_yk = 500 N/mm²; concrete cover = 40mm

Top reinforcement (Hogging moment)
Support A (No moment redistribution)
Effective depth (d) = 600 – 40 – 16 – 10 = 534 mm
d₂ = 40 + 8 + 10 = 58 mm

M_Ed = 761.24 kNm

But since the flange is in tension, we use the beam width to calculate the value of k (this applies to all support hogging moments)
k = M_Ed / (f_ckb_wd²) = (761.24 × 10⁶) / (35 × 400 × 534²) = 0.1906
z = d[0.5+ √((0.25 – 0.882(0.167))] = 0.82d = 0.82 × 534 = 437.88 mm
x = (d − z)/0.4 = (534 − 437.88)/0.4 = 240.3 mm

d₂/x = 58/240.3 = 0.241 < 0.38 (therefore reinforcement bar has yielded and f_sc = 0.87f_yk)

Since k < 0.167, compression is required
Area of compression reinforcement A_S2 = (M_Ed – M_lim) / (0.87f_yk (d – d₂))

M_lim = 0.167f_ckbd² = (0.167 × 35 × 400 × 534²) × 10^-6 = 666.69 kNm

A_S2 = ((761.24 – 666.69) × 10⁶) / (0.87 × 500 × (534 – 58)) = 457 mm²
Provide 3H16 Bottom (A_sprov = 603 mm²)

Area of tension reinforcement A_s1 = M_Rd / (0.87f_yk z) + A_S2
Where z = d[0.5+ √(0.25 – 0.882K’)]
K’ = 0.167
z = d[0.5+ √((0.25 – 0.882(0.167))] = 0.82d

A_s1 = M_Rd / (0.87f_yk z) + A_S2 = ( 666.69 × 10⁶) / (0.87 × 500 × 0.82 × 534) + 457 mm² = 3957 mm²

Provide 3H32mm + 4H25 mm Top (A_Sprov = 4376 mm²)