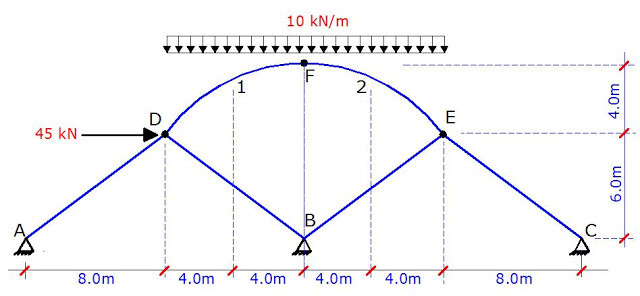
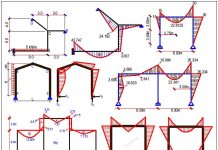
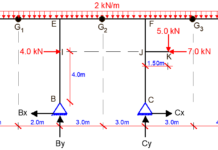
A parabolic arch structure is hinged on two interacting trusses as shown in the image above. The arch is also hinged at the crown (point F). We are expected to obtain the internal forces acting on the structure due to the externally applied uniform load on the arch, and the horizontal
concentrated load at point D. Since the arch is hinged on the truss, we can decompose the structure, and analyse the arch as a three-hinged arch, after which we transfer the support reactions from the arch to the truss. The detached arch structure is as shown below;
Support Reactions
∑ME = 0
16Dy – (10 × 162)/2 = 0
Therefore, Dy = 1280/16 = 80 KN
A little consideration from symmetry will also show that Ey = 80 KN
8Dy – 4Dx – (10 × 82)/2 = 0
8(80) – 4Dx – (10 × 82)/2 = 0
– 4Dx + 320 = 0
Therefore, Dx = 320/4 = 80 KN = Ex
Geometric Properties of the Arch Section
The ordinate of the arch at any given horizontal length section is given by;
y = [4yc (Lx – x2)] / L2
Where yc is the height of the crown of the arch
y = [(4 × 4) × (16x – x2)]/162 = x – (x2/16)
dy/dx = y’ = 1 – x/8
At x = 0; y = 0
y’ = 1 – 0/8 = 1
sinθ = y’/√(1 + y’2) = 1/√(1 + 12) = 0.7071
cosθ = 1/√(1 + y’2) = 1/√(1 + 12) = 0.7071
At x = 4m;
y = x – x2/16 = 4 – (42/16) = 3m
y’ = 1 – 4/8 = 0.5
sinθ = y’/√(1 + y’2) = 0.5/√(1 + 0.52) = 0.4472
cosθ = 1/√(1 + y’2) = 1/√(1 + 0.52) = 0.8944
At x = 8m;
y = x – x2/16 = 8 – (82/16) = 4m
y’ = 1 – 8/8 = 0
sinθ = y’/√(1 + y’2) = 0/√(1 + 0.52 ) = 0
cosθ = 1/√(1 + y’2) = 1/√(1 + 0) = 1.0
At x = 12m;
y = x – x2/16 = 12 – (122/16) = 3m
y’= 1 – x/8 = 1 – 12/8 = -0.5
sinθ = y’/√(1 + y’2) = (-0.5)/√(1 + 0.52) = -0.4472
cosθ = 1/√(1 + y’2) = 1/√(1 + 0.52 ) = 0.8944
At x = 16m;
y = x – x2/16 = 16 – (162/16) = 0
y’= 1 – 16/8 = 1 – 12/8 = -1.0
sinθ = y’/√(1 + y’2) = (-1.0)/√(1 + 12 ) = -0.7071
cosθ = 1/√(1 + y’2) = 1/√(1 + 12 ) = 0.7071
Internal Stresses in the Arch StructureBending Moment
MD = 0
M1 = (80 × 4) – (80 × 3) – (10 × 42)/2 = 0
MF = (80 × 8) – (80 × 4) – (10 × 82)/2 = 0
M2 = (80 × 12) – (80 × 3) – (10 × 122)/2 = 0
ME = 0
Shear force
Qi = ∑V cosθ – ∑H sinθ
QD = (80 ×0.7071) – (80 × 0.7071) = 0 (No shear)
Q1L = Q1R [80 – (10 × 4)] × 0.8944 – (80 × 0.4472) = 0 (No shear)
QF = [80 – (10 × 8)] × 1.0 – (80 × 0) = 0 (No shear)
Q2L = Q3R = [80 – (10 × 12)] × 0.8944 – (80 × -0.4472) = 0 (No shear)
QE = [80 – (10 × 16)] × 0.7071 – (80 × -0.7071) = 0 (No shear)
Axial force
Ni = -∑V sinθ – ∑H cosθ
ND = -(80 × 0.7071) – (80 × 0.7071) = -113.136 KN (Compression)
N1L = -[80 – (10 × 4)] × 0.4472 – (80 × 0.8944) = -89.44 KN
NF = -[80 – (10 × 8)] × 0 – (80 × 1) = -80 KN (Compression)
N2L = N3R = -[80 – (10 × 12)] × -0.4472 – (80 × 0.8944) = -89.44 KN
NE = -[80 – (10 × 16)] × -0.7071 – (80 × 0.7071) = -113.136 KN
We now transfer the reactive forces from the arch section to the the supporting trusses below;
θ = tan-1(6/8) = 36.869°
cosθ = 0.8
sinθ = 0.6
Analysis of Joint D
∑FX = 0
-35 – 0.8FAD + 0.8FDB = 0
– 0.8FAD + 0.8FDB = 35 —————- (1)
-80 – 0.6FAD – 0.6FDB = 0
– 0.6FAD – 0.6FDB = 80 —————- (2)
Solving (1) and (2) simultaneously;
FAD = -88.542 KN (Compression)
FDB = -44.792 KN (Compression)
Analysis of joint E
∑FX = 0
80 – 0.8FBE + 0.8FEC = 0
– 0.8FBE + 0.8FEC = 80 —————- (3)
∑FY = 0
-80 – 0.6FBE – 0.6FEC = 0
– 0.6FBE – 0.6FEC = 80 —————- (4)
Solving (3) and (4) simultaneously;
FBE = -16.667 KN (Compression)
FDB = -116.667 KN (Compression)
Support Reactions
Support A
∑FY = 0
Ay + 0.6FAD = 0
Ay – (0.6 × 88.542) = 0
Ay = 53.1252 KN
∑FX = 0
Ax + 0.8FAD = 0
Ax – (0.8 × 88.542) = 0
Ax = 70.8336 KN
Support B
∑FX = 0
Bx – 0.8FBD + 0.8FBE = 0
Bx – (0.8 × -44.792) + (0.8 × -16.667) = 0
Bx = -22.5 KN
∑FY = 0
By + 0.6FBD + 0.6FBE = 0
By – (0.6 × 44.792) – (0.6 × 16.667) = 0
By = -36.8754 KN
Support C
∑FY = 0
Cy + 0.6FEC = 0
Cy – (0.6 × 116.667) = 0
Cy = 70 KN
∑FX = 0
-Cx – 0.8FEC = 0
-Cx – (0.8 × -116.667) = 0
Cx = 93.333 KN
Equilibrium Verification
∑FY ↓ = (10 × 16) = 160 KN
∑FY ↑ = Ay + By + Cy = 53.1252 + 36.8754 + 70 = 160 KN
∑FX → = 45 + 70.833 = 115.833 KN
∑FX ← = 22.5 + 93.333 = 115.833 KN
Internal Stresses Diagram
As you can see, there are no bending moment and shear forces on the structure, therefore, the axial force diagram is as given below;