Stress Increment in Soil under a Pad Foundation

When foundations are constructed, they increase the net pressure in the soil. The knowledge of this stress increment is very important for estimating the settlement of foundations, and for the evaluation of lateral pressure on adjacent structures.

Boussinesq in 1883 solved the problem of stresses produced at any point in a homogeneous, elastic, and isotropic medium as the result of a point load applied on the surface of an infinitely large half-space. This has been extended into solving most of the problems of stresses that foundations impose on soils and for different types of loading, despite the fact that soils are practically neither homogeneous nor elastic.

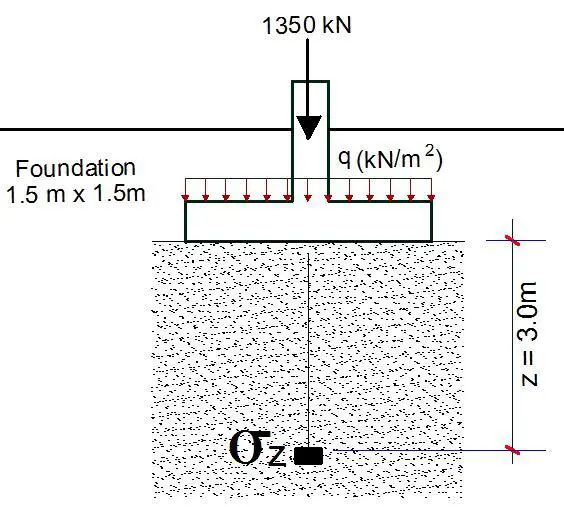
In this example, it is required to obtain the stress that a soil mass experiences at a depth of 3m under the pad foundation shown below.

The increment in the stress at any point below a pad foundation can be obtained by following the relationship below.

For example, let us consider the plan of a pad footing shown below. The loaded area can be divided into four rectangles A, B, C, and D, as shown. It is desired to determine the stress at a point below point 1 at depth z. Note that this point is very common to all four rectangles. The increment in stress at a depth z below point 1 due to each rectangular area can be calculated using the equation above.

The total stress increase caused by the entire loaded area is given by equation (2) below;

∆σ_z = q [I_3(A) + I_3(B) + I_3(C) + I_3(D)] ———- (2)

At the centre of a pad footing, this is given by;

∆σ_z = q I₄   ————– (3)

Where;

For the increment in stress at the centre of a rectangular footing, we can obtain the value of I₄ from the Table below (derived from the relationship above);

Therefore, for the example under consideration;
The service pressure (q) = P/A = (1350 kN) / (1.5m × 1.5m) = 600 kN/m²

b = B/2 = 1.5/2 = 0.75m
m₁ = L/B = 1.5m/1.5m = 1.0
n₁ = z/b = 3m/0.75m = 4.0

Reading from the table above;
I₄ = 0.108

∆σ_z = q I₄
∆σ_z = 600 × 0.108 = 64.8 kN/m²

Therefore, apart from the overburden pressure (geostatic stress), the stress at a depth of 3m under the pad foundation increased by 64.8 kN/m² due to the foundation load.

If you benefited from this post, connect with our facebook page at www.facebook.com/structville