Analysis of Continuous Beams with Partially Distributed Load Using Force Method and Clapeyron’s Theorem

For the continuous beam loaded as shown above, it is desired to find the bending moments at the critical points using force method (method of consistent deformations) and Clapeyron’s theorem (3 Moment Equation). We should however note that both methods are force methods (flexibility method) since we generally solve for unknown forces.

(1) By force method
Degree of static indeterminacy neglecting horizontal forces and reactions.

D = 2m + r – 2n
D = 2(3) + 4 – 2(4) = 2
Therefore the structure is indeterminate to the 2nd order.

Basic System
A basic system is a system that is statically determinate and stable. This obtained by removing the redundant supports at A and B, and replacing them with unit loads. See the figure below.

Case 1

Case 2
Bending moment on the basic system due to unit virtual load at support B

Case 3
Bending moment due to externally applied load on the basic system;

δ₁₁

δ₂₂

δ₁₁ = [1/6 × L × L(4L + L)] + [1/3 × L × L × L] = 3L³/2

δ_1P

δ_1P = [1/6 × qL²/16 × (2L + 2L) × L/2]] + [15/12 × qL²/16 × L × L/2] = 13qL⁴/384

δ_2P

δ_2P = [1/6 × qL²/16 × (L + L) × L/2] + [15/12 × qL²/16 × L/2× L/2] = 13qL⁴/768

The appropriate cannonical equation is given by;

δ₁₁X₁ +  δ₁₂X₂ + δ_1P = 0
δ₂₁X₁ +  δ₂₂X₂ + δ_2P = 0

Therefore;

(4L³)X₁ +  (3L³/2)X₂  = -13qL⁴/384
(3L³/2)X₁ +  (2L³/3)X₂  = -13qL⁴/768

On sloving the above equations simultaneously;

X₁ = 13qL/1920 KN

X₂ = -13qL/320 KN

The final moment values can now be computed;

M_f = M₁X₁ + M₂X₂ + M_P

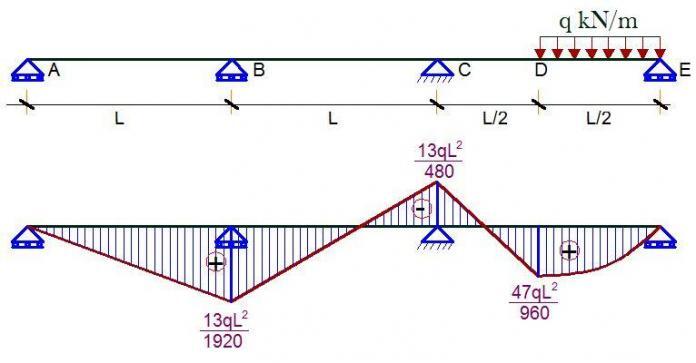
M_B = (13qL/1920 × L) + 0 + 0 = 13qL²/1920
M_C = (13qL/1920 × 2L) – (13qL/230 × L) + 0 = -13qL²/480
M_D = (13qL/1920 × L) – (13qL/230 × L/2) + qL²/16  = 47qL²/960

(2) By Clapeyron’s Theorem;

First of all, we draw the free bending moment diagram

By Clapeyron’s three moment equation (EI = constant, no sinking of support);

M_AL₁ + 2M_B + M_CL₂ + 6A₁X₁ + 6A₂X₂ = 0

Geometrical Properties of the free moment diagram (centroid)

SPAN A – C
M_A = 0
2M_B(L + L) + M_CL = 0
4M_B L + M_CL = 0 ——————– (1)

SPAN B-D
M_D = 0
M_BL + 2M_C(L + L) = [-6 × 7qL³/192 × 13L/128]/L
M_B L + 4M_CL =  -13qL³/128 ——————– (2)

Solving (1) and (2) simultaneously;
M_B =  13qL²/1920
M_C = -13qL²/480