Calculation of Effective Flange of Width of Beams

Clause 5.3.2.1 of EN 1992-1-1:2004 covers the calculation of the effective flange width of beams for all limit states. For T-beams, the effective flange width, over which uniform conditions of stress can be assumed, depends on the web and flange dimensions, the type of loading, the span, the support conditions and the transverse reinforcement. The effective width of the flange should be based on the distance lo between points of zero moments, which is shown in the Figure below (Figure 5.2 EN 1992-1-1:2004).

According to EC2, the length of the cantilever, l₃, should be less than half the adjacent span and the ratio of adjacent spans should lie between 0.667 and 1.5.

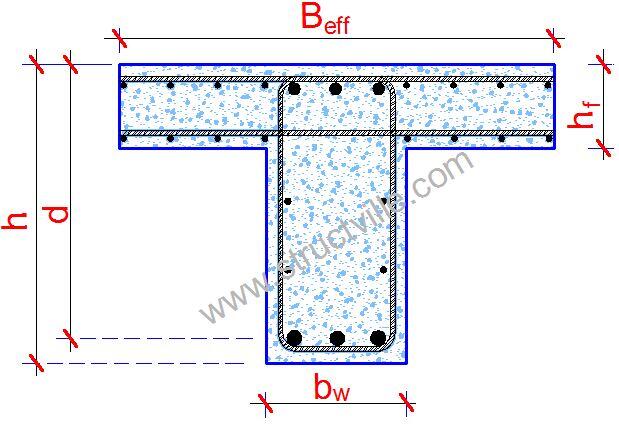
The flange width for T-beams and L-beams can be derived as shown below. The notations are shown in the figure below and above (Figure 5.3 EN 1992-1-:2004).

b_eff  = Σb_eff,i + b_w ≤ b ———– (1)

where;
b_eff,i = 0.2b_i + 0.1l_o ≤ 0.2l_o ———– (2)
and
b_eff,i ≤ b_i

Solved Example
Consider the floor plan shown below;
We are going to calculate the flange width of the various floor beams in the general arrangement.
All floor beams are 230mm x 450mm

External Beams
(1) Beams A:1-3 and D:1-3

b₁ = (6000 – 230)/2 = 2885 mm (there will be no b₂ since it is an L-beam)
l_o = (0.85 × 5000) = 4250 mm (assumed point of zero moment)

b_eff,1 = 0.2b_i + 0.1l_o = 0.2(2885) + 0.1(4250) = 577 + 425 = 1002 mm < (0.2 × 4250 = 850 mm)
Therefore take b_eff,i = 850 mm

b_eff  = Σb_eff,i + b_w ≤ b = 850 mm + 230 mm = 1080 mm < 3000 mm
Therefore effective flange width = 1080 mm

Comparing this answer with BS 8110-1:1997 (clause 3.4.1.5)
b_eff  = l_z/10 + b_w

Where l_z is the distance between points of zero moment (take as 0.85L = 4250 mm) in this case.
b_eff  = 4250/10 + 230 = 655 mm

(2) Beams 1:A-B

b₁ = (5000 – 230)/2 = 2385mm (there will be no b₂ since it is an L-beam)
l_o = (0.85 × 6000) = 5100 mm (assumed point of zero moment)

b_eff,1 = 0.2b_i + 0.1l_o = 0.2(2385) + 0.1(5100) = 477 + 510 = 987 mm < (0.2 × 5100 = 1020 mm) Therefore take b_eff,i = 987 mm

b_eff  = Σb_eff,i + b_w ≤ b = 987 mm + 230 mm = 1217mm < 2500 mm
Therefore effective flange width = 1080 mm

Comparing this answer with BS 8110-1:1997 (clause 3.4.1.5)
b_eff  = l_z/10 + b_w

Where l_z is the distance between points of zero moment (take as 0.85L = 5100 mm) in this case.
b_eff  = 5100/10 + 230 = 740 mm

(3) Beams 1:B-C

b₁ = (5000 – 230)/2 = 2385mm (there will be no b₂ since it is an L-beam)
l_o = (0.7 × 6000) = 4200 mm (assumed point of zero moment)

b_eff,1 = 0.2b_i + 0.1l_o = 0.2(2385) + 0.1(4200) = 477 + 420 = 897 mm < (0.2 × 4200 = 840 mm) Therefore take b_eff,i = 840 mm

b_eff  = Σb_eff,i + b_w ≤ b = 840 mm + 230mm = 1070mm < 2500mm
Therefore effective flange width = 1070mm

Comparing this answer with BS 8110-1:1997 (clause 3.4.1.5)
b_eff  = l_z/10 + b_w

Where l_z is the distance between points of zero moment (take as 0.7L = 4200mm) in this case.
b_eff  = 4200/10 + 230 = 650 mm

Internal Beams
(1) Beams B:1-3 and C:1-3

b₁ = (6000 – 230)/2 = 2885 mm
b₂ = (6000 – 230)/2 = 2885 mm
l_o = (0.85 × 5000) = 4250 mm (assumed point of zero moment)

b_eff,1 = 0.2b₁ + 0.1l_o = 0.2(2885) + 0.1(4250) = 577 + 425 = 1002 mm < (0.2 × 4250 = 850 mm)
b_eff,2 = 0.2b₂ + 0.1l_o = 0.2(2885) + 0.1(4250) = 577 + 425 = 1002 mm < (0.2 × 4250 = 850 mm)

Therefore take b_eff,1 = b_eff,2 = 850 mm

b_eff  = Σb_eff,i + b_w ≤ b = 850 + 850 + 230  = 1930 mm < 6000 mm
Therefore effective flange width = 1930 mm

Comparing this answer with BS 8110-1:1997 (clause 3.4.1.5)
b_eff  = l_z/5 + b_w

Where l_z is the distance between points of zero moment (take as 0.85L = 4250 mm) in this case.
b_eff  = 4250/5 + 230 = 1080 mm

(2) Beams 2:A-B

b₁ = (5000 – 230)/2 = 2385mm
b₂ = (5000 – 230)/2 = 2385mm
l_o = (0.85 × 6000) = 5100 mm (assumed point of zero moment)

b_eff,1 = 0.2b₁ + 0.1l_o = 0.2(2385) + 0.1(5100) = 477 + 510 = 987 mm < (0.2 × 5100 = 1020 mm)
b_eff,2 = 0.2b₂ + 0.1l_o = 0.2(2385) + 0.1(5100) = 477 + 510 = 987 mm < (0.2 × 5100 = 1020 mm)
Therefore take b_eff,1 = b_eff,2 = 987 mm

b_eff  = Σb_eff,i + b_w ≤ b = 987 + 987 + 230 mm = 2204mm < 5000mm
Therefore effective flange width = 2204 mm

Comparing this answer with BS 8110-1:1997 (clause 3.4.1.5)
b_eff  = l_z/5 + b_w

Where l_z is the distance between points of zero moment (take as 0.85L = 5100 mm) in this case.
b_eff  = 5100/5 + 230 = 1250 mm

(3) Beams 2:B-C

b₁ = (5000 – 230)/2 = 2385 mm
b₂ = (5000 – 230)/2 = 2385 mm
l_o = (0.7 × 6000) = 4200 mm (assumed point of zero moment)

b_eff,1 = 0.2b₁ + 0.1l_o = 0.2(2385) + 0.1(4200) = 477 + 420 = 897 mm < (0.2 × 4200 = 840 mm)
b_eff,2 = 0.2b₂ + 0.1l_o = 0.2(2385) + 0.1(4200) = 477 + 420 = 897 mm < (0.2 × 4200 = 840 mm)
Therefore take b_eff,i = b_eff,2 = 840 mm

b_eff  = Σb_eff,i + b_w ≤ b = 840 + 840 + 230 = 1910 mm < 5000mm
Therefore effective flange width = 1910 mm

Comparing this answer with BS 8110-1:1997 (clause 3.4.1.5)
b_eff  = l_z/5 + b_w

Where l_z is the distance between points of zero moment (take as 0.7L = 4200mm) in this case.
b_eff  = 4200/5 + 230 = 1070 mm

We are pleased that you visited today. Keep visiting us for new updates.