Sinking of Supports of Propped Cantilever Beams

Example
Let us consider a 6m cantilever that is supported on a roller at the free end. The roller support undergoes a vertical settlement of 25mm (downwards). We are to determine the additional bending moment at the fixed support due to the settlement. We will approach this problem using force and stiffness methods.

Solution
(a) By force method
A propped cantilever (roller support) is indeterminate to the 1st order. The adopted basic system for the structure is a simple 6m cantilever. We will now replace the redundant vertical reaction with a unit load, and the resulting bending moment diagram is as shown below.

The appropriate cannonical equation is given by;
δ₁₁X₁ + δ_1∆ = 0

Where;
δ₁₁ = Deformation at point 1 (free end) due to unit load at point 1
δ_1∆ = Deformation at point 1, due to settlement of Support = – EI(∆.S)

By Vereschagin’s rule;

δ₁₁ = (1/3) × 6 × 6 × 6 = 72

On the other hand;
δ_1∆ =  – EI(∆.S) = -22500 (1 × -0.025) = 562.5

Substituting into the canonical equation and solving;
72X₁ + 562.5 = 0
On solving;
X₁ = – 7.8125 kN (downward reaction)

With this reaction now known, the moment at support A due to the sinking of support;
M_A = – 7.8125 × 6 = -46.875 kNm (hogging moment)

(b) By stiffness method
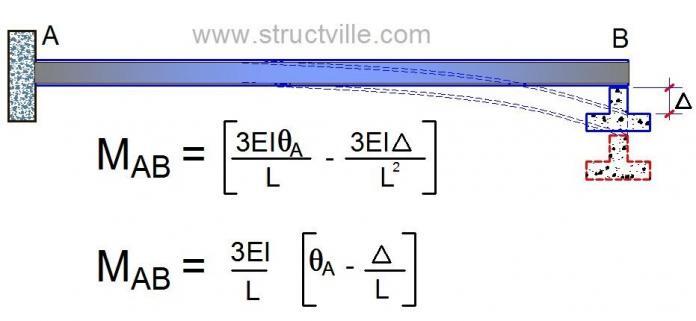
With support A fully fixed and support B simply supported, the general equation for bending moment at support A due to external load and settlement of support is given by;

M_AB = [(3EIθ_A/L) – (3EI∆/L²)] + F_AB

Where F_AB is the fixed end moment due to externally applied load = 0
Also θ_A = 0 since support A is fully fixed.
∆ = 25mm = -0.025m (negative due to downward settlement).

M_AB = [((3 × 22500)/6) × (-0.025/6)] = -46.875 kNm

Now, we obtained the answer above expressly because of very known facts. Since the bending moment at B zero, we may not pass through the stress of obtaining the rotation at support B. However for the sake of knowledge, let us apply a more general method which a lot of people might be more familiar with. Here, we will obtain the rotation (slope) at support B, and use it to obtain the bending moment at support A. We are initially assuming that all supports are fixed in the development of the slope deflection equations.

M_AB = EI/L[(4θ_A + 2θ_B – 6∆/L)] + F_AB
M_BA = EI/L[(2θ_A + 4θ_B – 6∆/L)] + F_BA

For equilibrium and compatibility;
M_BA = 0

We also know that θ_A = 0 (fixed support), and there is no external load being considered;

22500/6[4θ_B – (6 × -0.025)/6] = 0
15000θ_B + 93.75 = 0
Therefore, θ_B = -0.00625 radians

Substituting the value of θ_B into the slope deflection equation for  M_AB
M_AB = EI/L[(2θ_B ]
M_AB = 3750[(2 × -0.00625)] = 46.875 kNm

Thank you for reading to the end.