Structural Design of Slabless (Sawtooth) Staircase

Slabless staircases (also called sawtooth staircases) offer aesthetically pleasing alternatives in buildings, and are often a source of wonder to those who do not understand the design and detailing principles underlying their construction.  The processes of determining the design moments in sawtooth staircases have been presented in this post.

According to Reynolds and Steedman (2005), Cusens (1966) showed that if axial shortening is neglected, and the strain energy due to bending only considered, the mid span moment in a slabless staircase is given by the general expression;

where;
k₀ is the ratio of the stiffness of the tread to the stiffness of the tread
j = number of treads

If j is odd;

If j is even;

Design Example
Let us obtain the design forces in a slabless staircase with the following properties;
Thickness of tread and riser = 100mm
Height of riser = 175mm
Width of tread = 300mm
Number of treads = 7
Width of staircase = 1500mm

Load Analysis
Self weight of staircase;
{[(0.3 × 0.1) + (0.175 × 0.1)] / 0.3} × 24 = 3.8 kN/m²
Self weight of finishes = 1.2 kN/m²

At ultimate limit state;
n = 1.35gk + 1.5qk
n = 1.35(5) + 1.5(3) = 11.25 kN/m²

k₀ = 175/300 = 0.583

Reading from chart, the support moment coefficient can be taken as -0.086
The support bending moment is therefore;
M_s = 0.086 × 11.25 × 2.1² = 4.267 kN.m

j = 7 (odd)
The free bending moment is therefore
M_f = 1/8 × 11.25 × 2.1² × [(7² + 1)/7²] = 6.325 kNm

Therefore, the span moment = M_f – M_s = 6.325 – 4.267 = 2.058 kNm

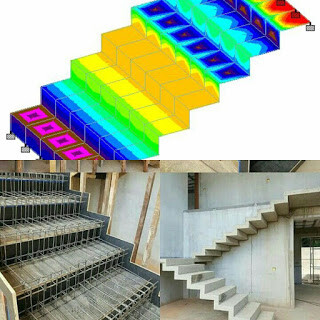
Comparing this answer with finite element analysis from Staad Pro;

The 3D rendering of the staircase is as shown below;

The linear elastic analysis of the structure gave the following results;

Longitudinal Bending Moment

Transverse Bending Moment