Plastic Analysis of Frames

The fully plastic moment of a section (M_p) is the maximum moment of resistance of a fully yielded cross-section. The yielded zone due to bending where infinite rotation can take place at a constant plastic moment (M_p) is called a plastic hinge.

In order to find the fully plastic moment of a yielded section, we normally employ the force equilibrium equation by saying that the total force in tension and compression at that section are equal. In frames, the plastic moment can be easily obtained using the kinematic method (upper bound theorem).

When a system of loads is applied to an elastic body, it will deform and show some resistance to deformation, and such a body is called a structure. On the other hand, if no resistance is set up against deformation, such as a body is said to have formed a mechanism. This can occur in structures such as beams and frames.

One of the fundamental conditions for plastic analysis of a framed structure is that the collapse load is reached when a mechanism is formed, in which the number of plastic hinges developed in the structure is sufficient to form a mechanism. The load factor (λ) at rigid plastic collapse is the lowest multiple of the design load which will cause the whole structure or part of it to form a mechanism.

It is important to realise that the number of independent mechanisms in a structure is related to the number of plastic hinge locations and the degree of redundancy of the system.

In beams, identification of critical spans in terms of M_p or load factor can be obtained using the static or kinematic method by considering simple beam mechanisms. But in framed structures, other types of mechanisms such as joint, sway, and gable mechanisms are also considered. Each of these mechanisms can occur independently, but it also possible for a critical collapse mechanism to develop by combination of the independent mechanisms.

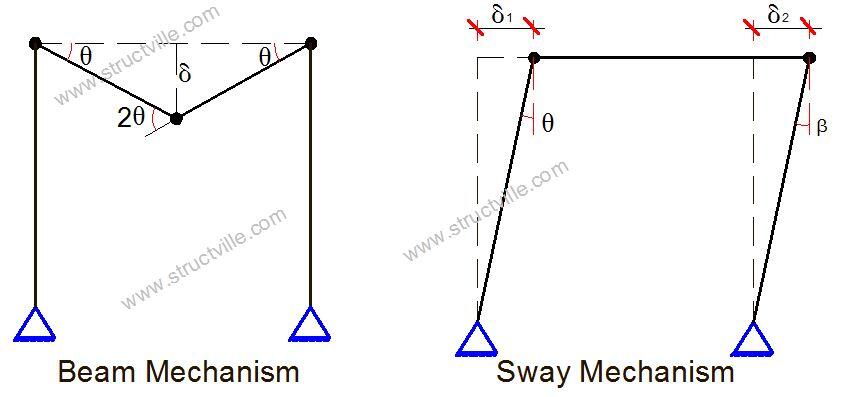
The purpose of combining mechanisms is to eliminate hinges that exist in the independent mechanism leaving only the minimum number required in the resulting combination to induce collapse.

The steps in the plastic analysis of frame structures are as follows;

1. Calculate the degree of static indeterminacy of the structure (R_D)
2. Calculate the number of possible plastic hinges (R_D + 1)
3. Identify the independent collapse mechanisms and evaluate them
4. Combine the independent mechanism and eliminate hinges where applicable
5. Obtain the critical plastic moment Mp which is the highest bending moment in the structure
6. Check for equilibrium and evaluate the reactive forces
7. Plot the final plastic moment diagram. No bending moment at any point in the structure should exceed the critical plastic moment.

Solved Example
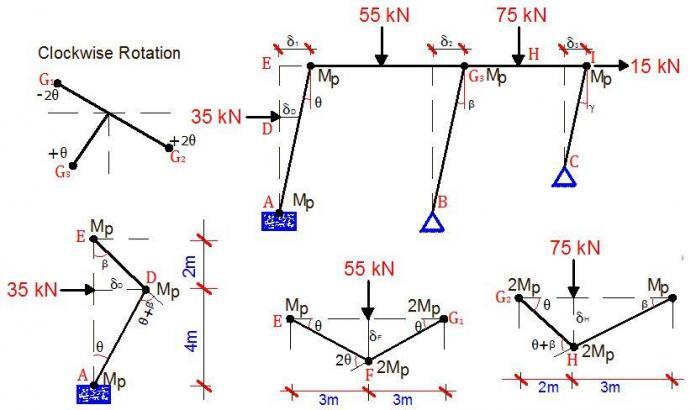
For the frame loaded as shown below, find the critical M_p value, and draw the collapse moment diagram. The loads are factored.

Degree of static indeterminacy
R_D = (3m + r) – 3n
m (number of members) = 4
r (number of support reactions) = 5
n (number of nodes) = 5
R_D = (3 × 4 + 5) – 3(5) = 2
Therefore the frame is indeterminate to the second order.

A little consideration will show that the possible places where we could have plastic hinges in the structure are at node B, section C, section D (just to the left), section D (just to the right), section D (below) and section F. Nodes A, E, and F are all natural hinges. Therefore, total number of possible hinges = 6

Hence, number of independent collapse mechanisms = 6 – 2 = 4

These independent mechanisms are listed below;
– 2 Beam mechanisms (span B – D and span D – G)
– 1 sway mechanism of the entire frame due to the horizontal load
– 1 joint mechanism

Analysis of the independent mechanisms

Mechanism 1

δ_C = 3 × θ = 3θ
Internal work done due to rotations at internal hinges at B, D, and C
Total internal work done (Wi) = Mpθ + Mpθ + 2Mpθ = 4Mpθ

External work done (We) = 115 × 3θ = 345θ

Let external work done = Internal work done
4Mpθ = 345θ
On solving, M_p = 345/4 = 86.25 kNm

Mechanism 2

δ_F = 3 × θ = 3θ
Internal work done due to rotations at internal hinges at B, and F. No work is done at G because it is a natural hinge.
Total internal work done (Wi) = Mpθ + 2Mpθ = 3Mpθ

External work done (We) = 74 × 3θ = 222θ

Let external work done = Internal work done
3Mpθ = 222θ
On solving, M_p = 222/3 = 74 kNm

Mechanism 3 (Sway)

δ₁ = 4 × θ = 4θ
Internal work done due to rotations at internal hinges at B, and D. No work is done at A, E, and G because they are all natural hinges.

Total internal work done (Wi) = M_pθ + M_pθ = 2Mpθ

External work done (We) = 25 × 4θ = 100θ

Let external work done = Internal work done
2M_pθ = 100θ
On solving, M_p = 100/2 = 50 kNm

Mechanism 4 (Joint Rotation)

Internal work done = M_pθ + M_pθ + M_pθ = 3M_pθ
External work done = 0 (no external work done)

Internal work done = M_pθ + M_pθ + M_pθ = 3M_pθ
External work done = 0 (no external work done)

Let us now consider the possible mechanism combination by preparing the table below

The critical M_p is therefore = 111.167 kNm (This was achieved after other combinations were considered but this was found to be the highest).

Note that by virtue of the combination, internal hinges at B, D₂, and D₃ were eliminated. So the critical collapse mechanism is as given below;

Note that the implication of our analysis above is that points C, F and D₁ are plastic hinges, with a full plastic moment of 111.167 kNm. While C and F are sagging, D₁ is hogging. No other bending moment in the structure should exceed this value. Once a higher moment is discovered, it means that the critical collapse moment was not appropriately obtained.

∑M_F^R = 0 (anti clockwise positive)
3V_G = 111.167
V_G = 37.056 kN

∑M_C^L = 0 (clockwise positive)
3V_A – 4H_A = 111.167 ———– (1)

∑M_D^L = 0 (clockwise positive)
6V_A – 4H_A – (115 × 3) = -111.67
6V_A – 4H_A = 233.833 ———– (2)

Solving (1) and (2) simultaneously;
V_A = 40.721 kN
H_A = 2.623 kN

∑M_A = 0 (clockwise positive)
12V_G + 6V_E – (74 × 9) – (115 × 3) – (25 × 4) = 0
6V_E = 666.328
V_E = 111.055 kN

∑F_x = 0
H_E = 25 + 2.623 = 27.623 kN

Bending Moment
You can verify that having obtained the support reactions, the bending moment diagram can easily be plotted without strenuous calculations.

Thank you for visiting Structville today, and God bless you.