Preliminary Plastic Analysis of Portal Frames

Steel portal frames provide economical solution for construction of industrial structures, warehouses, churches or other buildings with large enclosures. The loading scheme on portal frames usually includes dead load, wind load, imposed load, service loads, snow loads, imperfections, thermal loads, crane loads etc.

In the plastic analysis of portal frames, preliminary analysis is usually carried out to determine member sizes before detailed checks are carried out to determine the adequacy of the selected sections. Weller’s chart is usually used to quickly determine the plastic moments that can enable initial sizing of members. The simplicity of the charts depends on a series of three charts developed by Weller. The application of the method relies on the following assumptions;

(1) The rafter depth is approximately span / 55
(2) The hunch length is approximately span /10
(3) The rafter slope lies between 10° and 20°.
(4) The ratio of span to eaves height is between 2 and 5.
(5) The hinges in the mechanism are formed at the level of the underside of the haunch in the column and close to the apex.

Each chart requires a knowledge of the geometry of the frame and the design loading as input data in order to determine approximate sizes for the column and rafter member.

Application Example

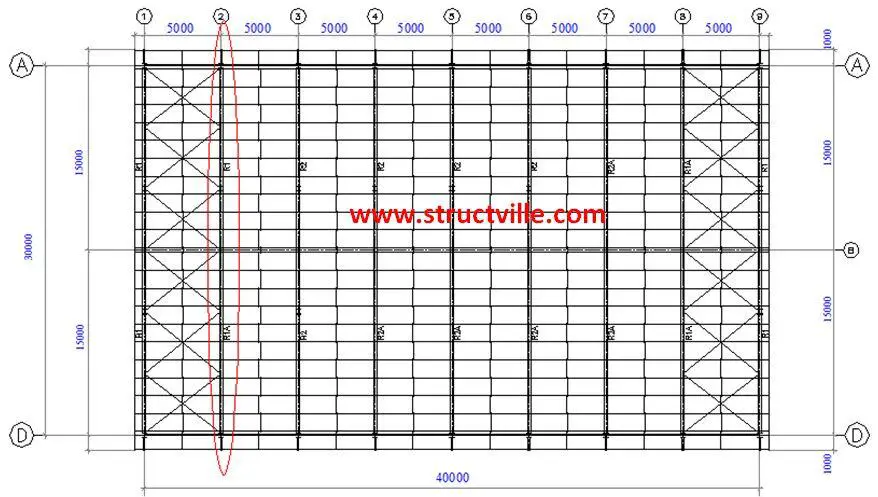Fig 1: General Arrangement of Steel Structure

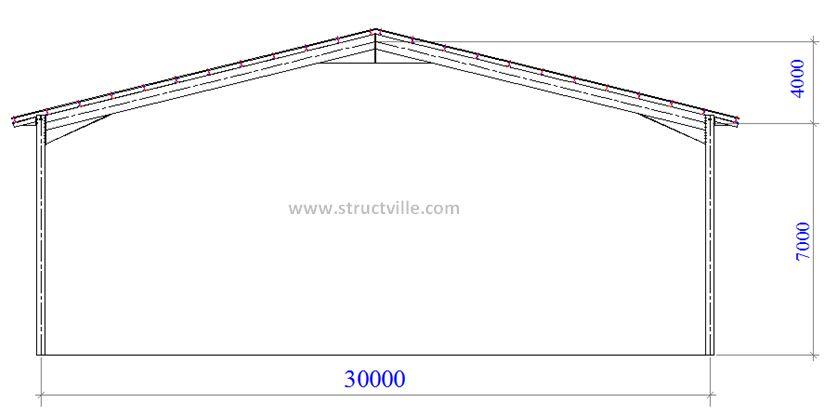Fig 2: Portal Frame

Length of building = 40 m
Width of building = 30 m
Height to eaves = 7.0 m
Height to roof top = 11.0 m

Consider the portal frame on gridline 2. The gravity load on the portal frame is analysed as follows;

Load Analysis 
(1) Dead Load
Aluminium roof sheeting = 0.04 kN/m²
Insulation (assume gypsum boards per 10 mm thickness) = 0.077 kN/m²
Other permanent services = 0.15 kN/m²
Steel purlins (take) = 0.03 kN/m²
Self weight of rafter (take) = 0.15 kN/m²
Total = 0.447 kN/m² on slope

Angle of inclination of roof = 15°
Load on plan = 0.447/cos 15° = 0.4627 kN/m²

Spacing of portal frame = 5 m centre to centre
Therefore dead load on roof gk = 0.4627 kN/m² x 5m = 2.31 kN/m

(2) Imposed Load
According to BS 6399 Part 3, for roof with slope less than 30°, a minimum imposed load of 0.6 kN/m² on plan should be provided as long as no access except for cleaning and maintenance is provided.

For this design, let us adopt an imposed load of 0.75 kN/m²

qk = 0.75 kN/m²

Imposed load on roof = 0.75 x 5m = 3.75 kN/m

At ultimate limit state;
p = 1.4gk + 1.6qk = 1.4(2.31) + 1.6(3.75) = 9.234 kN/m

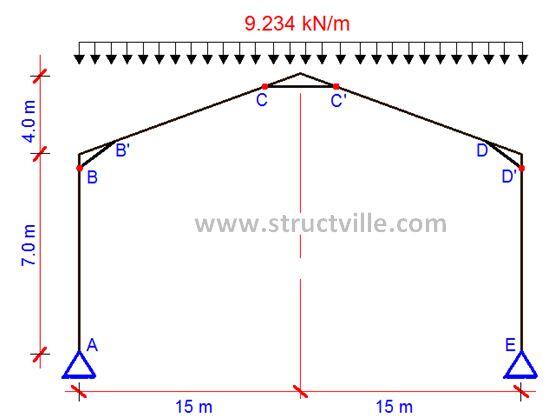Fig 3: Portal Frame with ULS Gravity Load

Step by Step Analysis

(a) Calculate the span/height to eaves ratio = L/h
Span/height to eaves ratio L/h = 30/7 = 4.285

(b) Calculate the rise/span ratio = r/L
Height of Rise / span ratio r/L = 4/30 = 0.133

(c) Calculate the total design load FL on the frame and then calculate FL², where F is the load per unit length on plan of span L
Ultimate gravity load = 9.234 kN/m (see Fig. 3)
Total load on the frame (wL) = 9.234 x 30 = 277.02 kN
Parameter wL² = 9.234 x 30² = 8310.6 kNm

(d) From Fig 4 (Chart 1) obtain the horizontal force ratio H_FR at the base from r/L and L/h

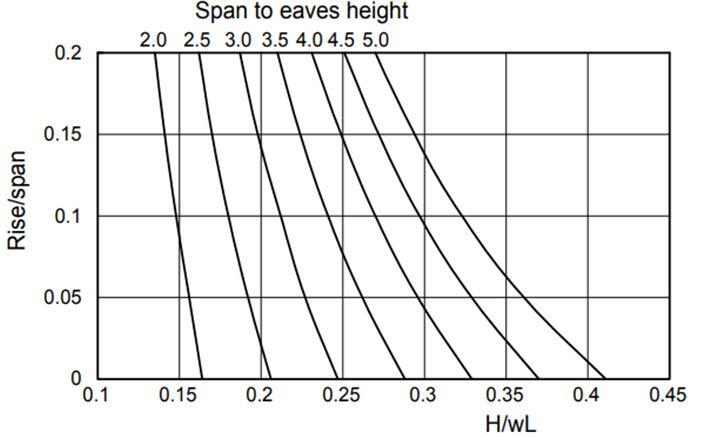Fig 4: Chart 1

H/wL = 0.27
Hence, horizontal force ratio H_FR = 0.27

(e) Calculate the horizontal force at the base of span H = H_FR wL
Hence, H = 0.27 x 277.02 = 74.795 kN

(f) From Fig 5 (Chart 2), obtain the rafter M_p ratio M_pR from r/L and L/h.

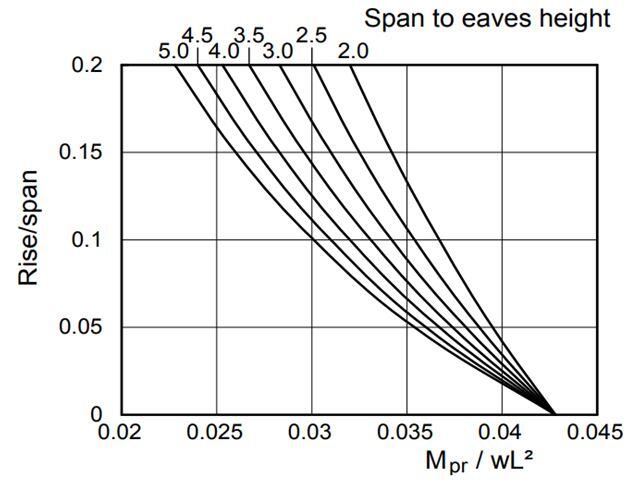Fig 5: Chart 2

Rafter M_pR/wL²  ratio = 0.028

(g) Calculate the M_p required in the rafter from M_p(rafter) = M_pR x wL²
M_p,Rafter = 0.028 x 8310.6 = 232.696 kNm

(h) From Fig 6 (Chart 3), obtain the column M_p ratio from r/L and r/h

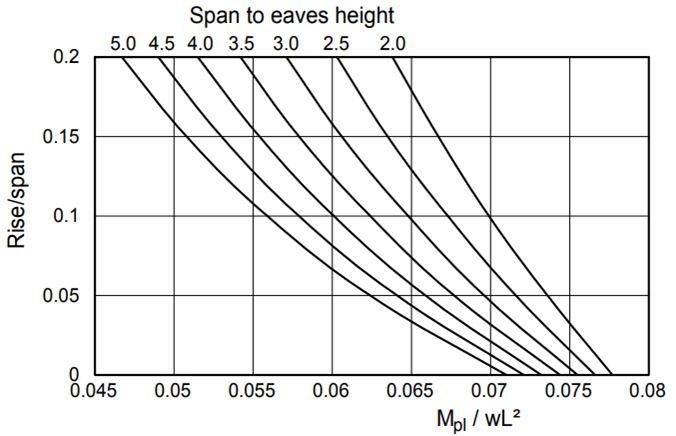Fig 6: Chart 3

Column M_pC/wL² ratio = 0.057

(i) Calculate the M_p required in the column from M_p,Column = M_pC x wL²
M_p,Column  = 0.057 x 8310.6 = 473.70 KNm

(j) Determine the plastic moduli for the rafter W_pl,y,R and the column W_pl,y,C from
W_pl,y,R = M_p,Rafter /f_y
W_pl,y,C = M_p,Column/f_y

Where f_y is the yield strength = 275 Mpa.

Using the plastic moduli, the rafter and column sections may be chosen from the range of plastic sections as so defined in the section books