Structural Design of Flat Slabs

Flat slabs are slabs are two-way concrete slabs that are supported directly by columns without floor beams. Therefore, they offer economical solutions to larger floor spans in reinforced concrete buildings. The columns supporting the slab panel may or may not have drop panels.

Drop panels are particularly advantageous in situations where substantial negative moments occur at supports or where punching shear stresses are critical and the use of punching reinforcement is undesirable.

There are many advantages of flat slabs such as increased headroom, easier flow of mechanical and electrical services, ease in construction of formwork, faster construction etc. Unlike traditional beam and slab systems, flat slabs eliminate the use of floor beams, resulting in a cleaner, more open space.

Analysis of Flat Slabs

The following methods are usually employed in the analysis of flat slabs:

• simplified coefficient approaches,
• equivalent frame analysis,
• yield line theory,
• grillage analysis, and
• finite element methods.

The application of simplified coefficients is subject to specific conditions outlined in Annex I of BS EN 1992-1-1. Yield line and finite element methods are particularly well-suited for computer-based analysis. Given this, this discussion will concentrate on the use of simplified coefficients.

In the Eurocodes, the analysis of flat slab is the same as that recommended in BS 8110. According to clause 3.7.2.7 of BS 8110, the simplified method can be used for flat slabs that the lateral stability is not dependent on the slab and columns provided that the following conditions are met;

(1) The slab is loaded with a single load case of all the panels loaded with maximum ultimate load. This means that the following requirements must be satisfied (clause 3.5.2.3);
(a) The area of each bay exceeds 30 m²
(b) The ratio of the characteristic imposed load to the dead load does not exceed 1.25
(c) The imposed load does not exceed 5 kN/m²

(2) There are at least three rows of approximately equal panels in the direction  being considered
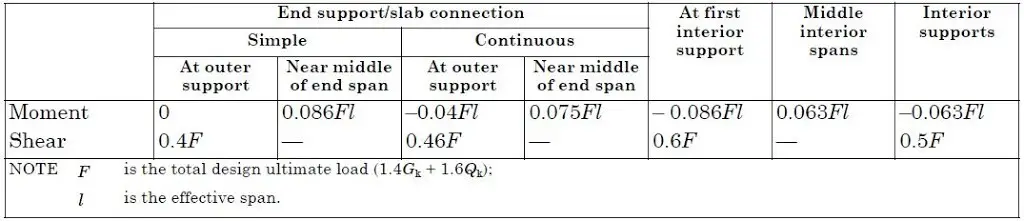
(3)  Moments at supports can be reduced by 0.15Fh_c

Design Example of Flat Slab

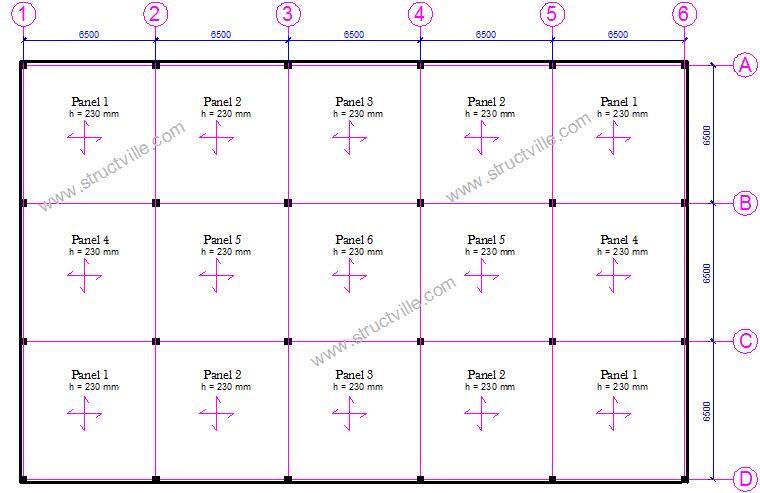
In this article, we are going to analyse gridline 2 (same as gridline 5) of the flat slab general arrangement that is given above with the following data;

The thickness of slab = 230 mm (governed by deflection requirements)
f_ck = 30 Mpa
f_yk = 500 Mpa
Imposed load = 3 kN/m²
Concrete cover = 30 mm
Size of columns = 300 x 300 mm

Load Analysis

Permanent Actions
Self weight = 0.23 × 25 = 5.75 kN/m²
Finishes = 1.2 kN/m²
Partition allowance = 1.2 kN/m²
Total permanent actions g_k = 8.15 kN/m²

Variable Actions
Imposed floor load q_k = 3 kN/m²

Total load on the floor F = 1.35g_k + 1.5q_k = 1.35(8.15) + 1.5(3) = 15.5 kN/m²

Effective span of the slab = 6500 – 2(300/2) + 2(230/2) = 6430 mm
Width of bay = 6500 mm
Width of column strip = 2(l_x/4)= 2(6500/4) = 3250 mm
Width of middle strip = 6500 – 1625 – 1625 = 3250 mm

F = 15.5 × 6.5 × 6.5 = 654.875 kN

A little consideration will show that the slab under consideration met the conditions for use of coefficients.

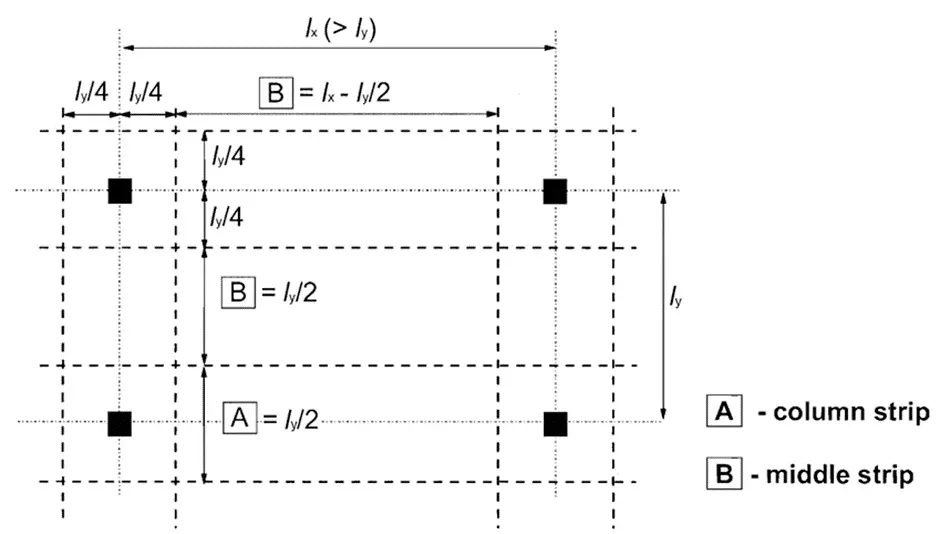
For reference on how the panel was divided into middle and column strips, see Figure 3.12 of BS 8110-1:1997.

Bending Moments (In the longitudinal direction)
Sagging – First Span
M = 0.086 × 654.87 × 6.43 = 362.13 kNm

Hogging – First interior support
M = -0.086 × 654.87 × 6.43 = -362.13 kNm

The apportionment of moments between column strips and middle strips is shown in Table 2:

	Hogging	Sagging
Column strip	70%	50%
Middle strip	30%	50%

(Column Strip)
Hogging moment (Support B and C)
M_Ed = 0.7 × (362.13/3.25) = -77.99 kNm/m

Sagging moment:
M_Ed = 0.5 × (362.13/3.25) = 55.71 kNm/m

(Middle Strip)
Hogging moment (Support B and C)
M_Ed = 0.3 × (362.13/3.25) = -33.427 kNm/m

Sagging moment:
M_Ed = 0.5 × (362.13/3.25) = 55.71 kNm/m

Structural Design – Flexure: column strip and middle, sagging

M_Ed = 55.71 kNm/m
d = h – C_c – ϕ/2

Assuming ϕ16mm bars will be employed for the construction
d = 230 – 30 – 8 = 192 mm; b = 1000mm (designing per unit width)

k = M_Ed/(f_ckbd²) = (55.71 × 10⁶)/(30 × 1000 × 192²) = 0.086

Since k < 0.167 No compression reinforcement required

z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.086)] = 0.917d = 0.917 × 192 = 176.12 mm

A_s1 = M_Ed/(0.87f_ykz) = (55.71 × 10⁶)/(0.87 × 500 × 176.12) = 727 mm²/m

Provide H16mm @ 200 mm c/c BOT (A_Sprov = 1005 mm²/m)

Check the minimum area of steel required;
f_ctm = 0.3 × f_ck^2⁄3 = 0.3 × 30^2⁄3 = 2.89 N/mm² (Table 3.1 EC2)

A_s,min = 0.26 × f_ctm/f_yk × b × d = 0.26 × 2.89/500 × 1000 × 192 = 289 mm²/m
Check if A_s,min < 0.0013 × b × d (250 mm²/m)
Since, A_s,min = 250 mm², the provided reinforcement is adequate.

Check for deflection
We check for deflection of flat slabs at the long span of the slab

Allowable L/d = N × K × F1 × F2 × F3 ≥ Actual L/d
K = 1.2 for flat slabs
ρ = A_s,req/bd = 727/(1000 × 192) = 0.003786 > 10^-3√f_ck (0.00547)

Since ρ > ρ₀
l/d = [11 + 1.5√f_ck(ρ₀/(ρ – ρ’)) + 0.0833√f_ck(ρ₀/ρ)^0.5] if ρ > ρ₀
ρ₀/ρ= 0.00547/0.003786 = 1.44

N = [11 + 1.5√(30) × 1.444 + 0.0833√30 × (1.444)^0.5] = 11 + 11.86 + 0.548 = 23.4

F1 = 1.0 (b_eff/b_w = 1.0)
F2 = 1.0 (no brittle partitions)
F3 = 310/σ_s ≤ 1.5

where:

σ_su = (500/1.15) × (8.15 + 0.3 × 3)/15.5 = 253.856 MPa
σ_s = σ_su × (A_s,req/A_s,prov) = 253.856 × (727/1005) = 183.6 N/mm²
β_s = 310/183.6 = 1.688 > 1.5 (take 1.5)

Therefore allowable L/d = 23.4 × 1.2 × 1.0 × 1.0 × 1.5 = 42.12

Actual L/d = 6430/192 = 33.49

Therefore, deflection is okay.

Flexure: column strip, hogging
M_Ed = 77.99 kNm/m

k = M_Ed/(f_ckbd²) = (77.99 × 10⁶)/(30 × 1000 × 192²) = 0.0705
Since k < 0.167 No compression reinforcement required

z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.0705)] = 0.933d = 0.933 × 192 = 179.2 mm

A_s1 = M_Ed/(0.87f_ykz) = (77.99 × 10⁶)/(0.87 × 500 × 179.2) = 1000 mm²/m

Provide T16mm @ 175 mm c/c Top (A_Sprov = 1149 mm²/m)

(c) Flexure: Middle strip, hogging
M_Ed = 33.43 kNm/m

k = M_Ed/(f_ckbd²) = (33.43 × 10⁶)/(30 × 1000 × 192²) = 0.030
Since k < 0.167 No compression reinforcement required

z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.030)] = 0.95d = 0.95 × 192 = 182.4 mm

A_s1 = M_Ed/(0.87f_ykz) = (33.43 × 10⁶)/(0.87 × 500 × 182.4) = 421 mm²/m
Provide T12mm @ 200 mm c/c Top (A_Sprov = 565 mm²/m)

Perpendicular to edge of slab at edge column
Design transfer moment to column M_t = 0.17 b_ed²f_ck
b_e = c_z + y = 300 + 300 = 600 mm

M_t = 0.17 × 600 × 192² × 30 × 10⁻⁶ = 112.8 kNm
k = M_Ed/(f_ckbd²) = (112.8 × 10⁶)/(30 × 600 × 192²) = 0.1699

z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.1699)] = 0.82d = 0.82 × 192 = 157.44 mm

A_s1 = M_Ed/(0.87f_ykz) = (112.8 × 10⁶)/(0.87 × 500 × 157.44) = 1647 mm²/m
This reinforcement to be placed within c_x + 2c_y = 900 mm

Try H16T1 U-bars in pairs @ 100 (A_sprov = 2010 mm²) local to column (max. 200 mm from column)

Punching Shear Check

See worked example on punching shear verification of flat slabs.