Analysis of Beams on Elastic Foundation

Introduction

Fig 1: Schematic representation of beam on elastic foundation

For instance, the beam shown in Fig. 1 will deflect due to the externally applied load, and produce continuously distributed reaction forces in the supporting medium. The intensity of these reaction forces at any point is proportional to the deflection of the beam y(x) at that point via the constant k_s:

Where k_s is the soil’s modulus of subgrade reaction which is the pressure per unit settlement of the soil (unit in kN/m²/m).

If we assume that the beam under consideration has a constant cross section with constant width b which is supported by the foundation. A unit deflection of this beam will cause reaction equal to k_s.b in the foundation, therefore the intensity of distributed reaction (per unit length of the beam) will be:

R(x) = b.k_s.y(x) = k.y(x)                    (2)

where k = k₀.b is the constant of the foundation, known as Winkler’s constant, which includes the effect of the width of the beam, and has unit of kN/m/m.

The general 4th order differential equation for beam on elastic foundation is given by equation (3);

The homogenous equation is given by;

EI(d⁴y)/dx⁴ + k.y = 0

(d⁴y)/dx⁴ + 4β⁴y = 0

Where β = ∜(k/4EI) = (k/EI)^(1/4)

The general solution for the equation is available, which is given by;
y = e^βx (C₁sinβx + C₂cosβx) + e^-βx(C₃sinβx + C₄cosβx)

Warren and Richard (2002) published tables containing equations for analysing beams on elastic foundation subjected to different loads. The method described in the book has been employed to analyse a beam on elastic foundation and compare the results with Staad Pro software.

Solved Example
A 600mm x 400mm rectangular beam is resting on a homogenous soil of modulus of subgrade reaction ks = 10000 kN/m²/m. The beam is 10m long, and carrying a concentrated load of W =  300 kN from the left hand side. Neglecting the self weight of the beam, and assuming freely supported ends, obtain the bending moment at the point of the concentrated load. Take modulus of elasticity of concrete Ec = 21.7 x 10⁶ kN/m².

Solution 
Second moment of area of concrete beam I_B = (bh³)/12 = (0.4 × 0.6³)/12 = 7.2 x 10^-3 m⁴
Flexural rigidity of the beam E_cI_B = 21.7 × 10⁶ × 7.2 × 10^-3 = 156240 kN.m²
β = (bk_s/4EI)^(1/4) = [(0.4 × 10000)/(4 × 156240)]^(1/4) = 0.2828
βl = 0.2828 × 10 = 2.828 m; β(l – a) = 0.282(10 – 3) = 1.979

Where a is the distance of the concentrated load from the left end of the beam.
Since βl < 6.0, we can use Table 8.5 of Roark’s Table for Stress and Strain (Warren and Richard, 2002).

For a beam with both ends free;
R_A = 0; M_A = 0

The equations for bending moment and shear force along the beam is as given below;

Mx = M_AF₁ + R_A/2βF₂ – y_A2EIβ²F₃ – θ_AEIβF₄ – W/2βF_a2
Vx = R_AF₁ – y_A2EIβ³F₂ – θ_AEIβ²F₃ – M_AβF₄ – WF_a1

Where;
θ_A (rotation at point A) = [W/(2EIβ²)] × [(C₂C_a2 – 2C₃C_a1)/C₁₁]
y_A (vertical deflection at point A) = [W/(2EIβ³)] × [(C₄C_a1 – C₃C_a2)/C₁₁]

We can therefore compute the constants as follows;
C₂ = coshβl.sinβl + sinhβl.cosβl = [cosh(2.828) × sin(2.828)] + [sinh(2.828) × cos(2.828)] = (8.485 × 0.3084) + (8.426 × –0.9512 ) = –5.398

C₃ = sinhβl.sinβl = (8.426 × 0.3084) = 2.5985

C₄ = coshβl.sinβl – sinhβl.cosβl = [cosh(2.828) × sin(2.828)] + [sinh(2.828) × cos(2.828)] = (8.485 × 0.3084) – (8.426 × –0.9512) = 10.631

C_a1 = coshβ(l – a).cosβ(l – a) = cosh(1.974) × cos(1.974) = 3.669 × -0.392 = -1.438

C_a2 = coshβ(l – a).sinβ(l – a) + sinhβ(l – a).cosβ(l – a) = [cosh(1.974) × sin(1.974)] + [sinh(1.974) × cos(1.974)] = (3.669 × 0.9198) + (3.530 × -0.392) = 1.9909

C_a3 = sinhβ(l – a).sinβ(l – a) = (3.530 × 0.9198) = 3.247

C₁₁ = sinh²βl – sin²βl = 8.4262 – 0.30842 = 70.902

θ_A = W/(2EIβ²) × [(C₂C_a2 – 2C₃C_a1)/C₁₁]
θ_A = [300/(2 × 156240 × 0.2828² ) × [(–5.398 × 1.9909) – (2 × 2.5985 × –1.438)/70.902] = (0.012 × –0.0462) = -0.0005544 radians

y_A (vertical deformation at point A) = [W/(2EIβ³)] × [(C₄C_a1 – C₃C_a2)/C₁₁]
y = [300/(2 × 156240 × 0.2828³)] × [(10.631 × –1.438) –2.5985 × 1.9909)/70.902] = (0.0424 × –0.2885) = –0.01223 m = -12.23 mm

Bending moment at point C
Substituting the values of deflection and slope into the equation for bending moment (note that the first and second terms of the equation goes to zero since R_A = M_A = 0);

Mx = – y_AEIβ²F₃  – θ_AEIβF₄ – W/2βF_a2
Mx = – (–0.01223 × 2 × 156240 × 0.28282)F₃ – (– 0.0005544 × 156240 × 0.2828)F₄ – 300/(2 × 0.2828)F_a2

Mx = 305.638F₃ + 24.495F₄ – 530.410F_a2

Substituting F₃, F₄, and F_a2 (see Table 8.5, Warren and Richard, 2002) into the equation;

Mx = 305.638(sinhβx.sinβx) + 24.495(coshβx.sinβx – sinhβx.cosβx) – 530.410[coshβ(x –a).sin β(x –a) + sinh β(x –a).cos β(x –a)]

The bending moment under the concentrated load (point C);
x = 3m; (x – a) = 3 – 3 = 0

βx = 0.8484
Mx = 305.638[sinh(0.8484) × sin(0.8484)] + 24.495[cosh(0.8484) × sin(0.8484) – sinh(0.8484) × cos(0.8484)]

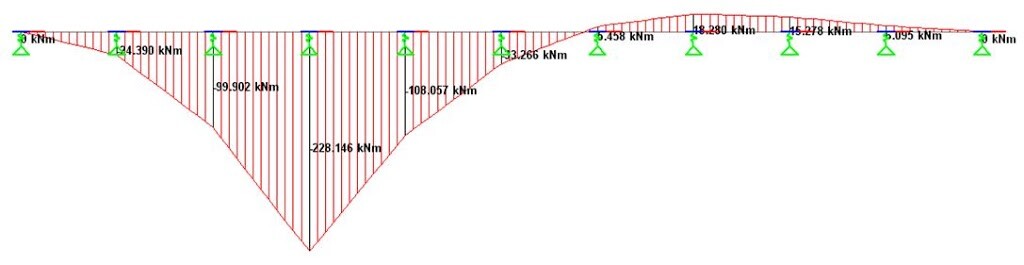
Mc = 305.638 (0.953 × 0.750) + 24.495(1.382 × 0.750 – 0.9539 × 0.6611) = 218.45 + 9.942 = 228.392 kN.m

Verification
This manual calculation has been verified using Staad Pro software. The steps adopted were as follows:

(1) Modelling
The 10m beam was modelled as a one dimensional line element connected by nodes at 1m length interval. This was to represent/attach soil springs at 1m interval.