Equivalent horizontal forces (EHF) are not strictly actions, but are forces that are applied to a frame in combination with other actions to model the effect of frame imperfections. Another alternative of doing this is to model the frame out of plumb. According to clause 5.3.2(6) of Eurocode 3, if a frame is sensitive to second order effects, member imperfection must be modelled in the analysis if the member has a moment resisting joint. In this post, we are going to show how to model the effects of imperfection for gravity actions in portal frames.
Determination of EHF
According to clause 5.3.2(3) of EC3, for frames sensitive to buckling in a sway mode the effect of imperfections should be allowed for in frame analysis by means of an equivalent imperfection in the form of an initial sway imperfection and individual bow imperfections of members. The imperfections may be determined from:
ϕ = ϕ0 αh αm
Where ϕ0 = 1/200
αh = 2/√h (h is the height of the structure in metres)
αm = √[0.5(1+ 1/m)] (where m is the number of columns in the row)
Solved Example
Model the effect of imperfection in the frame shown in Figure 1 using the equivalent horizontal force approach
Columns – UB 610 x 229 x 125
Rafters – UB 533 x 210 x 92
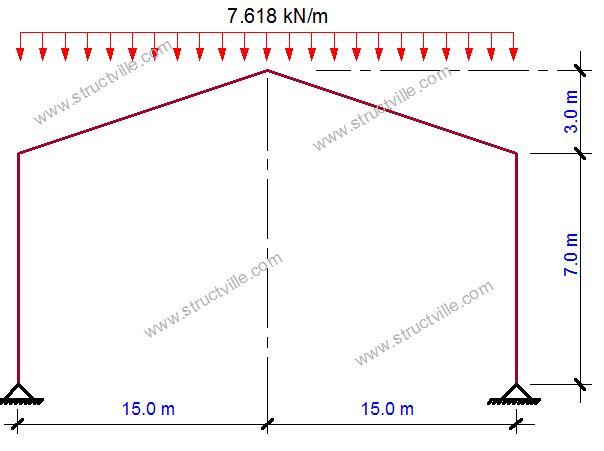
When analysed under the gravity action shown above, the following reactive forces and bending moment diagram was obtained.
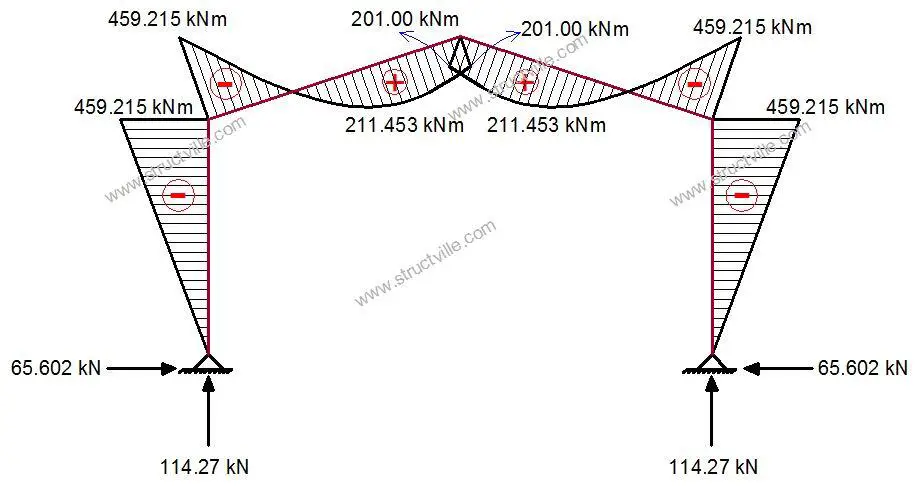
For the example above;
αh = 2/√h = 2/√7 = 0.755 (h is the height of the structure in metres)
αm = √[0.5(1 + 1/m)] (where m is the number of columns in the row)
αm = √[0.5(1 + 1/2)]= 0.8660
Therefore;
ϕ = (1/200) × 0.755 × 0.8660 = 0.0032
The equivalent horizontal forces are calculated as:
HEHF = ϕVEd
However, sway imperfections may be ignored where HEd ≥ 0.15VEd
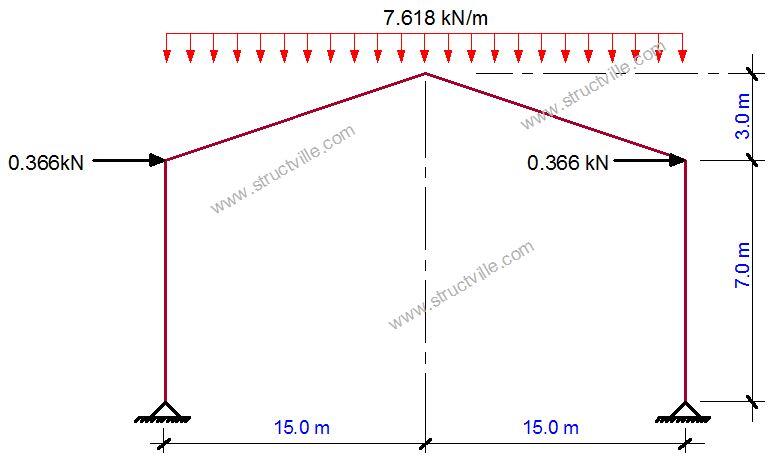
Choosing to incorporate the effect of imperfection in our analysis, the equivalent horizontal force is given by;
HEHF = 0.0032 × 114.27 = 0.366 kN
We will now model and analyse the frame for load combination 1 with the effects of imperfection included. The analysis will be done with the base pinned.
The resulting bending moment diagram with the effect of imperfection is given below;
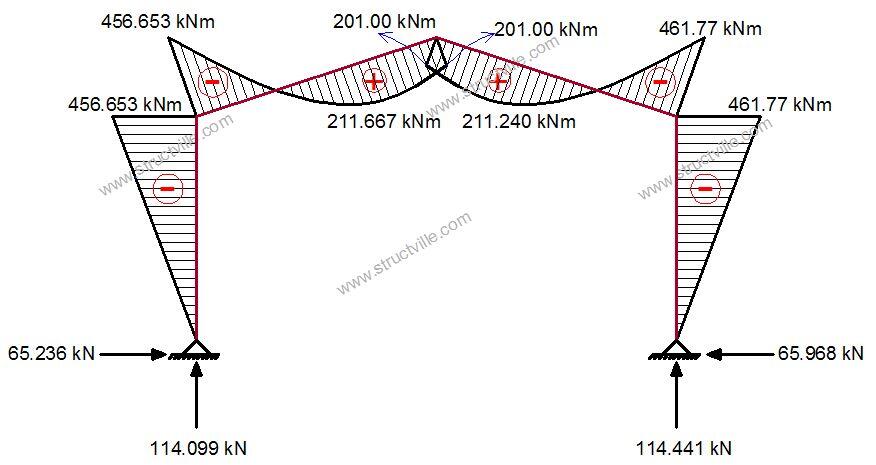
A little consideration of the above results will show that the effects of imperfection can be safely ignored in the design of the structure. Thank you for visiting Structville today.










