A structure is a system of connected parts designed to resist load. Kinematical analysis is very important in the evaluation of the capacity of a structure to resist external loads. This concept is concerned with the rigid (unchangeable) part of a structure which may be made up of straight members, curved members, etc, and how they are connected to each other. The connection of members in a structure could be by the means of links, hinges, or fixed joints. Hence, the arrangement of structural members and their connection conditions define whether a structure is geometrically unchangeable (stable) or geometrically changeable (unstable).
In a geometrically unchangeable structure, any distortion of the structure occurs only with the deformation of its members. It means that this type of structure with absolutely rigid members cannot change its form. The simplest geometrically unchangeable structure is a triangle, which contains the pin-joined members. However, in a geometrically changeable structure, any finite distortion of the structure occurs without the deformation of its members. The simplest geometrically changeable system is formed as hinged four-bar linkage.
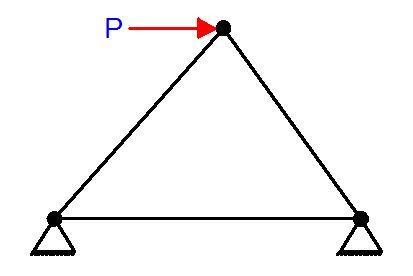
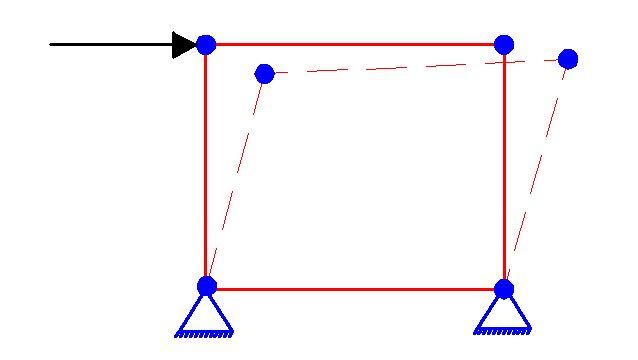
It may be recalled from statics that a structure or one of its members is in equilibrium when it maintains a balance of force and moment. In general, this requires that the force and moment equations of equilibrium be satisfied in a coplanar system of forces as follows;
∑Fx = 0
∑Fy = 0
∑Mi = 0
Here ∑Fx and ∑Fy represent, respectively, the algebraic sums of the x and y components of all the forces acting on the structure or one of its members, and ∑Mi represents the algebraic sum of the moments of these force components about an axis perpendicular to the x–y plane (the z-axis) and passing through point i. When all the forces in a structure can be determined strictly from the three equations of equilibrium, the structure is referred to as statically determinate. Structures having more unknown forces than available equilibrium equations are called statically indeterminate.
The required constraint of a structure is such a constraint which when removed changes the kinematical characteristic of the structure. It means that the entire unchangeable structure transforms into changeable. Note that constraint assumes not only the supports but the elements of a structure as well. For example, the elimination of any member of a simple truss can transforms it from unchangeable to changeable. A redundant constraint of a structure is such a constraint which when removed do not change a kinematical characteristic of the structure. It means that the entire unchangeable structure remains the unchangeable, and changeable structure remains a changeable one. Therefore, the presence of a redundant constraint is a characteristic of a statically indeterminate structure.
Generally, for a coplanar structure there are at most three equilibrium equations for each part, so that if there is a total of n parts and r force and moment reaction components, we have;
r = 3n (statically determinate structures)
r > 3n (statically indeterminate structures)
r < 3n (unstable)
Trusses
There are some formulas available for determining the degree of static determinacy of trusses.
D = s + m – 2n (plane trusses)
D = s + m – 3n (space trusses)
Where;
D = Degree of static indeterminacy
s = Number of support reactions
m = number of members
n = number of nodes
Examples
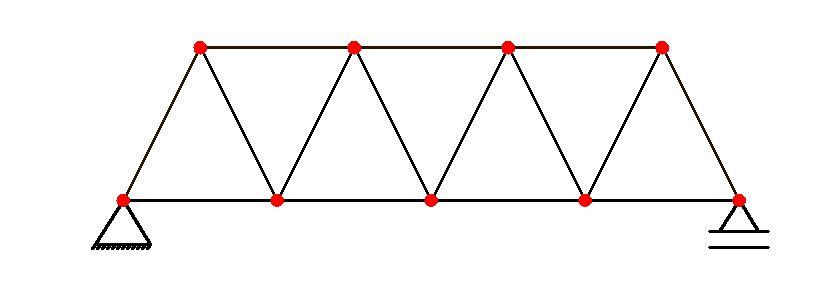
s = 3
m = 15
n = 9
D = 3 + 15 – 2(9) = 0 (statically determinate)
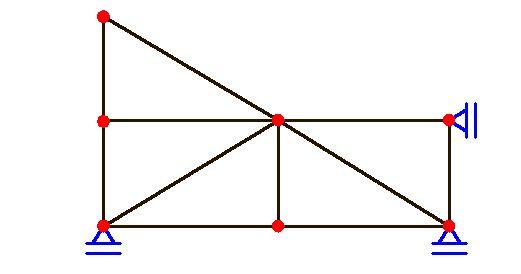
s = 3
m = 11
n = 7
D = 3 + 11 – 2(7) = 0 (statically determinate)
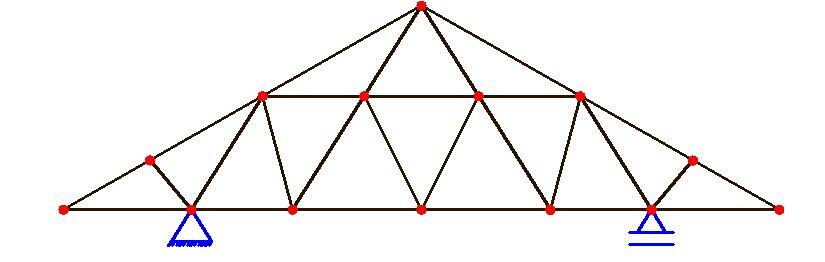
s = 3
m = 26
n = 14
D = 3 + 26 – 2(14) = 1 (statically indeterminate to the first order)
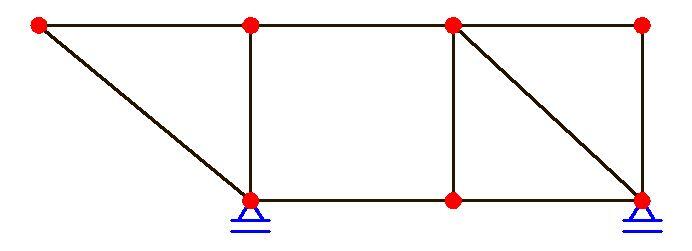
s = 2
m = 10
n = 7
D = 2 + 10 – 2(7) = -2 (unstable)
Beams and frames
For beams and framed structures, the formula below can be used to check the degree of static indeterminacy of the structure.
D = s + i + 3m – 3p
Where;
D = Degree of static indeterminacy
s = Number of support reactions
i = number of internal forces in hinges (usually 2 per internal hinge)
m = number of closed loops without hinges
p = number of parts
Examples
(1)

s = 6
i = 4 (2 internal hinges)
m = 0 (no closed loop)
p = 3 (3 parts)
D = 6 + 4 + 0 – 3(3) = 1 (statically indeterminate to the first order)
(2)

s = 6
i = 6 (3 internal hinges)
m = 0 (no closed loop)
p = 4 (4 parts)
D = 6 + 6 + 0 – 3(4) = 0 (statically determinate)
(3)

s = 5
i = 4 (2 internal hinges)
m = 0 (no closed loop)
p = 3 (3 parts)
D = 5 + 4 + 0 – 3(3) = 0 (statically determinate)
(4)
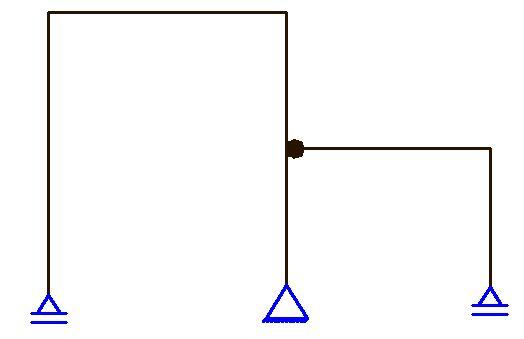
s = 4
i = 2 (1 internal hinge)
m = 0 (no closed loop)
p = 2 (2 parts)
D = 4 + 2 + 0 – 3(2) = 0 (statically determinate)
(5)
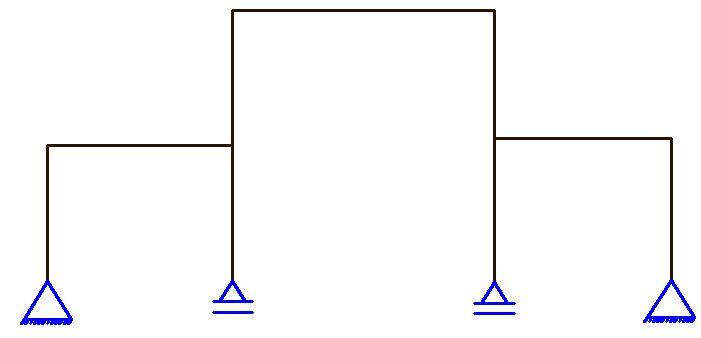
s = 6
i = 0 (no internal hinge)
m = 0 (no closed loop)
p = 1 (1 part)
D = 6 + 0 + 0 – 3(1) = 3 (statically indeterminate to the 3rd order)
(6)

s = 6
i = 0 (no internal hinge)
m = 3 (3 closed loops)
p = 1 (1 part)
D = 6 + 0 + 3(3) – 3(1) = 12 (statically indeterminate to the 12th order)
3D Frames
For 3D structures, the formula below can be used to check the degree of static indeterminacy of the structure.
D = s + i + 6m – 6p
Where;
D = Degree of static indeterminacy
s = Number of support reactions
i = number of internal forces in hinges (usually 2 per internal hinge)
m = number of closed loops without hinges
p = number of parts
Example
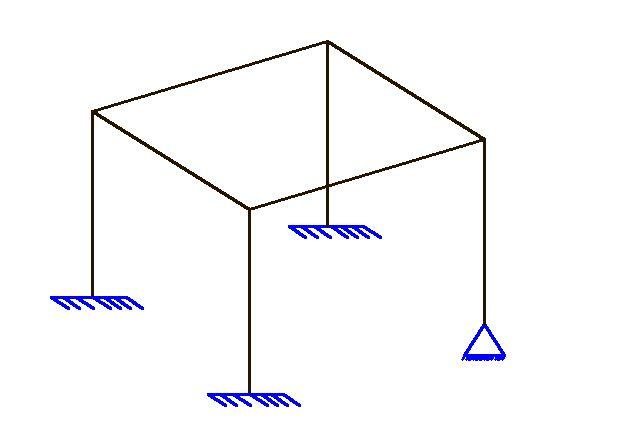
s = 11
i = 0 (no internal hinge)
m = 1 (1 closed loop)
p = 1 (1 part)
D = 11 + 0 + 6(1) – 6(1) = 11 (statically indeterminate to the 11th order)
Thank you for visiting Structville today and God bless you.










I find this article very useful for my study.
You are highly welcome